
题目列表(包括答案和解析)
5.(2009年高考安徽理综)大爆炸理论认为,我们的宇宙起源于137亿年前的一次大爆炸.除开始瞬间外,在演化至今的大部分时间内,宇宙基本上是匀速膨胀的.上世纪末,对1A型超新星的观测显示,宇宙正在加速膨胀.面对这个出人意料的发现,宇宙学家探究其背后的原因,提出宇宙的大部分可能由暗能量组成,它们的排斥作用导致宇宙在近段天文时期内开始加速膨胀.如果真是这样,则标志宇宙大小的宇宙半径R和宇宙年龄t的关系,大致是下面哪个图象( )
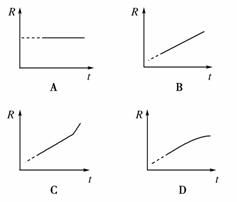
[解析] 题目提供的信息是宇宙先匀速膨胀,后加速膨胀,反映到R-t图象上就是图象的斜率先是不变的,后来斜率逐渐变大,所以应该选C项.
[答案] C
4.(2010陕西西安铁一中月考)如下图所示的位移(s)-时间(t)图象和速度(v)-时间(t)图象中,给出四条曲线1、2、3、4代表四个不同物体的运动情况,关于它们的物理意义,下列描述正确的是( )
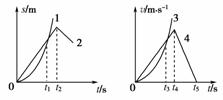
A.图线1表示物体做曲线运动
B.s-t图象中t1时刻v1>v2
C.v-t图象中0至t3时间内3和4的平均速度大小相等
D.两图象中,t2.t4时刻分别表示2、4开始反向运动
[解析] 能够用位移-时间图象和速度-时间图象表示的运动只有正、负方向之分,故均为直线运动,A项错;在位移-时间图象中,切线的斜率表示物体速度的大小,故s-t图象中t1时刻1物体的速度大于2物体的速度,B项正确;根据平均速度的定义,在相同时间内位移较大的物体平均速度较大,在v-t图象中,图线和坐标轴所围面积表示物体的位移,因此在0至t3时间内4物体的位移大于3物体的位移,故两物体平均速度不等,C项错;在速度-时间图象中纵坐标的正负表示速度的方向,因此在t4时刻4物体开始减速,并非改变方向,D项错.
[答案] B
3.
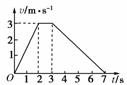
(2010广东省深圳市高三摸底考试)如右图是物体做直线运动的v-t图象,由图象可得到的正确结论是( )
A.t=1 s时,物体的加速度大小为1 m/s
B.t=5 s时,物体的加速度大小为0.75 m/s
C.第3 s内物体的位移为1.5 m
D.物体在加速过程的位移比减速过程的位移大
[解析] 由v-t图象可得0-2 s内物体的加速度为1.5 m/s2,A错;2-3 s内物体的加速度为0;3-7 s内物体的加速度为0.75 m/s2,故选项B正确.0-2 s物体的位移为3 m;2-3 s物体的位移为3 m;3-7 s物体的位移为6 m,则减速过程的位移比加速过程的位移大,C、D错.
[答案] B
2.
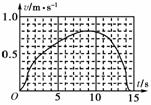
(2010年潍坊期中考试)某实验装置将速度传感器与计算机相结合,可以自动作出物体运动的图象.某同学在一次实验中得到的运动小车的速度-时间图象如右图所示,由此图象可知( )
A.小车先做匀加速运动,后做匀减速运动
B.小车运动的最大速度约为0.8 m/s
C.小车的最大位移在数值上等于图象中曲线与t轴所围的面积
D.小车做曲线运动
[解析] 速度-时间图象中图线的斜率表示加速度,图线与坐标轴所围面积表示位移,选项C正确;因为图线是一段曲线,选项A错误;据图象知小车运动的最大速度约为0.8 m/s,选项B正确;据图象知速度始终不小于零,说明小车做直线运动,选项D错误.
[答案] BC
1.一列车沿直线轨道从静止出发由A地驶向B地,并停在B地,列车做加速运动时,其加速度的最大值为a1;做减速运动时,其加速度的绝对值的最大值为a2.要让列车由A地到B地所用的时间最短,图中列车的v-t图象应是(其中tan α=a1;tan β=a2)( )
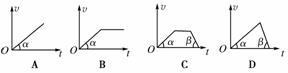
[解析] 分析题意可知先加速后减速的运动方式是用时最短的.
[答案] D
16.(12分)(2009年高考全国卷Ⅱ)如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速的大小和方向会与正常情况有微小偏离,重力加速度在原竖直方向(即PO方向)上的投影相当于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.
(1)设球形空腔体积为V,球心深度为d(远小于地球半径),=x,求空腔所引起的Q点处的重力加速度反常.
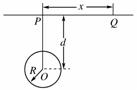
(2)若在水平地面上半径为L的范围内发现:重力加速度反常值在δ与kδ(k>1)之间变化,且重力加速度反常的最大值出现在半径为L的范围的中心.如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积.
[解析] (1)如果将近地表的球形空腔填满密度为ρ的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常可通过填充后的球形区域产生的附加引力
G=Δg①
来计算,式中m是Q点处某质点的质量,M是填充后球形区域的质量,
M=ρV②
而r是球形空腔中心O至Q点的距离
r=③
Δg在数值上等于由于存在球形空腔所引起的Q点处重力加速度改变的大小.Q点处重力加速度改变的方向沿OQ方向,重力加速度反常Δg′是这一改变的竖直方向上的投影
Δg′=Δg④
联立①②③④式得
Δg′=⑤
(2)由⑤式得,重力加速度反常Δg′的最大值和最小值分别为(Δg′)max=⑥
(Δg′)min=⑦
由题设有
(Δg′)max=kδ,(Δg′)min=δ⑧
联立⑥⑦⑧式得,地下球形空腔球心的深度和空腔的体积分别为d=⑨
V=⑩
[答案] (1) (2)
15.(12分)如右图所示,一个质量为m=0.6 kg的小球,以某一初速度v0从图中P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧轨道(不计空气阻力,进入时无机械能损失).已知圆弧半径R=0.3 m,图中θ=60°,小球到达A点时的速度v=4 m/s,取g=10 m/s2,试求:
(1)小球做平抛运动的初速度v0;
(2)判断小球能否通过圆弧最高点C;若能,求出小球到达圆弧轨道最高点C时对轨道的压力FN.
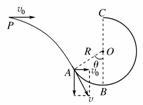
[解析] (1)将小球到达A点的速度分解如右图所示,则有v0=vcos θ=2 m/s.
(2)若小球能到达C点,由动能定理有-mgR(1+cos θ)=mv-mv2
可得vc= m/s>= m/s,故小球能到达最高点C
在最高点,由牛顿第二定律有:F′N+mg=m
代入数据得:F′N=8 N
由牛顿第三定律有:FN=-F′N=-8 N,方向竖直向上.
[答案] (1)2 m/s (2)能到达 -8 N 方向竖直向上.
14.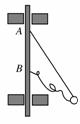 (10分)如右图所示,一个质量为m的小球由两根细绳拴在竖直转轴上的A、B两处,AB间距为L,A处绳长为L,B处绳长为L,两根绳能承受的最大拉力均为2mg,转轴带动小球转动.则:
(10分)如右图所示,一个质量为m的小球由两根细绳拴在竖直转轴上的A、B两处,AB间距为L,A处绳长为L,B处绳长为L,两根绳能承受的最大拉力均为2mg,转轴带动小球转动.则:
(1)当B处绳子刚好被拉直时,小球的线速度v为多大?
(2)为了不拉断细绳,转轴转动的最大角速度ω为多大?
(3)若先剪断B处绳子,让转轴带动小球转动,使A处绳子与转轴的夹角从45°开始,直至小球能在最高位置做匀速圆周运动,则在这一过程中,小球机械能的变化为多大?
[解析] (1)B处绳刚好被拉直时,A处绳与杆的夹角θ=45°,则有FAcos θ=mg,FAsin θ=m所以v=.
(2)转轴以最大角速度ω转动时,B绳拉力为FB=2mg,A绳拉力不变,则FAcos θ=mg,FAsin θ+FB=mω2L
解得:ω=.
(3)小球在最高位置运动时,F′A=2mg,F′Acos α=mg,则α=60°
由F′Asin α=m得vt=
ΔE=mg·L(cos θ-cos α)+
所以ΔE=mgL.
[答案] (1) (2) (3)mgL

13.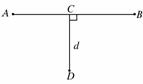 (10分)(2010年江苏无锡调研)早期人类狩猎的主要工具为标枪.如图,一只野兔(高度不计)以速度v1=20 m/s沿AB向右匀速奔跑,猎手隐藏在与直线AB相距d=9.0 m处的D点准备投掷.当野兔到达C点时,猎手沿水平方向投出一支标枪,标枪的投出点距离地面高度为h=1.8 m,忽略空气阻力,重力加速度g=10 m/s2.若刚好射中野兔,求:
(10分)(2010年江苏无锡调研)早期人类狩猎的主要工具为标枪.如图,一只野兔(高度不计)以速度v1=20 m/s沿AB向右匀速奔跑,猎手隐藏在与直线AB相距d=9.0 m处的D点准备投掷.当野兔到达C点时,猎手沿水平方向投出一支标枪,标枪的投出点距离地面高度为h=1.8 m,忽略空气阻力,重力加速度g=10 m/s2.若刚好射中野兔,求:
(1)野兔被射中时与C点的间距L;
(2)标枪的初速度v2的大小.
[解析] (1)标枪做平抛运动,有h=gt2 ①
野兔被射中时与C点的间距L=v1t ②
由①②可得L=12 m ③
(2)标枪的水平射程s=v2t ④
由几何关系s= ⑤
由④⑤可得v2=25 m/s ⑥
[答案] (1)12 m (2)25 m/s
12.(8分)(2010年上海师大附中)在右图所示的实验装置中,横杆能够绕竖直轴旋转,横杆在转动过程中,由于摩擦阻力的作用,横杆会越转越慢.在横杆的一端装有宽度为d=0.005 m的竖直“挡光圆柱”,当“挡光圆柱”通过光电门时,光电门就记录挡光的时间间隔,“挡光圆柱”宽度与挡光时间之比,可以近似认为是“挡光圆柱”在该时刻的速度.横杆每转一圈,光电门就记录一次“挡光圆柱”挡光时间.在一次实验中记录下横杆转动圈数n和每次挡光的时间t,并计算出“挡光圆柱”在该时刻的速度以及速度的平方(部分数据如表中所示).请计算表中当n=5时,v2=________m2/s2;如果继续测量“挡光圆柱”的速度,那么当n=15时,“挡光圆柱”的速度为__________m/s;“挡光圆柱”速度大小v与横杆转动圈数n的关系为____________
|
n |
t(10-3s) |
v=d/t(m/s) |
v2(m2/s2) |
|
1 |
2.778 |
1.80 |
3.24 |
|
2 |
2.826 |
… |
3.13 |
|
3 |
2.877 |
… |
3.02 |
|
4 |
2.931 |
… |
2.91 |
|
5 |
2.988 |
… |
|
|
6 |
3.049 |
… |
2.69 |
|
7 |
3.113 |
… |
2.58 |
|
8 |
3.181 |
… |
2.47 |
|
9 |
3.255 |
… |
2.36 |
|
10 |
3.333 |
… |
2.25 |
|
… |
… |
… |
… |
[答案] 2.80 m2/s2 1.30 m/s
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com