8.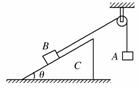 如右图所示，倾角为θ的斜面体C置于水平面上，B置于斜面上，通过细绳跨过光滑的定滑轮与A相连接，连接B的一段细绳与斜面平行，A、B、C都处于静止状态．则(　)

A．B受到C的摩擦力一定不为零

B．C受到水平面的摩擦力一定为零

C．不论B、C间摩擦力大小、方向如何，水平面对C的摩擦力方向一定向左

D．水平面对C的支持力与B、C的总重力大小相等

[解析]　以B物体为研究对象，沿斜面方向受到重力沿斜面方向向下的分力、绳的拉力和静摩擦力，静摩擦力的大小等于重力沿斜面方向向下的分力与拉力的合力，所以可能为0，可能沿斜面向上或向下，A项错误；利用整体法可知不论B、C间摩擦力大小、方向如何，水平面对C的摩擦力方向一定向左，B项错误，C项正确；同理，在竖直方向利用整体法判断水平面对C的支持力等于B、C的总重力大小减去拉力在竖直方向上的分力，D项错误．

[答案]　C

7.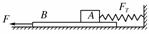 如右图所示，一个木块A放在长木板B上，长木板B放在水平地面上，有恒力F作用下，长木板B以速度v匀速运动，水平的弹簧秤的示数为F_T.下列有关摩擦力的说法正确的是(　)

A．木块受到的滑动摩擦力的大小等于F

B．木块受到的静摩擦力的大小等于F_T

C．若长木板B以2v的速度匀速运动时，木块受到的摩擦力的大小等于2F_T

D．若用2F的力作用在长木板B上，木块受到的摩擦力的大小仍等于F_T

[解析]　若用2F的力作用在长木板B上，木块受到的摩擦力的大小仍等于F_T.

[答案]　D

6. 如右图所示，质量为m₁的木块在质量为m₂的长木板上滑行，长木板与地面间动摩擦因数为μ₁，木块与长木板间动摩擦因数为μ₂，若长木板仍处于静止状态，则长木板受地面摩擦力大小一定为(　)

A．μ₁(m₁+m₂)g　　　B．μ₂m₁g

C．μ₁m₁g　 　　　　　　　D．μ₁m₁g+μ₂m₂g

[解析]　木块在木板上滑行，木板上表面所受滑动摩擦力F_f＝μ₂m₁g；木板处于静止状态，水平方向上受到木板对木板的滑动摩擦力和地面对木板的静摩擦力，根据力的平衡条件可知，地面对木板的静摩擦力的大小等于木块对木板的滑动摩擦力的大小，B项正确．

[答案]　B

5. (2008年高考全国卷Ⅱ)如右图，一固定斜面上两个质量相同的小物块A和B紧挨着匀速下滑，A与B的接触面光滑．已知A与斜面之间的动摩擦因数是B与斜面之间动摩擦因数的2倍，斜面倾角为α，B与斜面之间的动摩擦因数是(　)

A.tan α　　　 　B.cot α

C．tan α　 　　　　　D．cot α

[解析]　对A和B进行受力分析可知，A、B两物块受到斜面的支持力均为mgcos α，所受滑动摩擦力分别为F_fA＝μ_Amgcos α、F_fB＝μ_Bmgcos α，对整体受力分析结合平衡条件可得2mgsin α＝μ_Amgcos α+μ_Bmgcos α，且μ_A＝2μ_B，解得μ_B＝tan α，故答案为A.

[答案]　A

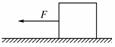
4. 如右图所示，一物体置于水平地面上静止不动，若用水平向左的力F＝5.0 N拉物体，物体仍静止，下述结论正确的是(　)

A．物体受到的合外力增加5.0 N

B．物体对水平面的压力增加5.0 N

C．物体对水平面的作用力大小增加5.0 N

D．物体受到水平面的静摩擦力是5.0 N

[解析]　物体一直处于静止平衡状态，受到合外力为零不变，物体对水平面的压力大小不变(等于物体受到的重力的大小)，由平衡条件可知物体受到的静摩擦力与水平方向的拉力大小相等，为5.0 N，A、B均错，D对；物体对水平面的作用力有压力与静摩擦力，方向互相垂直，即物体对水平面的作用力是这两个力的合力，不在同一直线上的力应用矢量平行四边形定则计算，而不能用代数方法运算，C错．

[答案]　D

3. 2008年初我国南方发生罕见的雪灾，导致大量交通车辆受阻，为解决这一问题，有的车辆轮胎上安装了防滑链，下列叙述正确的是(　)

A．装防滑链主要目的是增大车辆重力，从而增大摩擦力

B．装防滑链主要目的是增大车辆与地面接触面积，从而增大摩擦力

C．装防滑链主要目的是增大车辆与路面间粗糙程度，增大摩擦力

D．以上叙述均不正确

[答案]　C

2．卡车上装着一只集装箱，不计空气阻力，下面说法正确是(　)

A．当卡车开始运动时，卡车对集装箱的静摩擦力使集装箱随卡车一起运动

B．当卡车匀速运动时，卡车对集装箱的静摩擦力使集装箱随卡车一起运动

C．当卡车匀速运动时，卡车对集装箱的静摩擦力等于零

D．当卡车制动时，卡车对集装箱的静摩擦力等于零

[答案]　AC

1.如右图所示，质量m＝20 kg的物体，在粗糙水平面上向左运动，物体与水平面间的动摩擦因数μ＝0.1，物体同时还受到大小为10 N方向向右的水平拉力F的作用，则水平面对物体的摩擦力(g取10 m/s²)(　)

A．10 N，水平向左　 　　B．20 N，水平向左

C．20 N，水平向右　 　　　　　D．30 N，水平向右

[答案]　C

16.

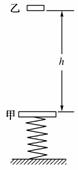
(12分)(2010年华中科大附中)质量m＝1.0 kg的甲物体与竖直放置的轻弹簧的上端连接，弹簧下端固定在地面上，如右图所示．质量m＝1.0 kg的乙物体从甲物体正上方，距离甲物体h＝0.40 m处自由落下，撞在甲物体上在极短的时间内与甲物体粘在一起(不再分离)向下运动．它们到达最低点后又向上运动，上升的最高点比甲物体初始位置高H＝0.10 m．已知弹簧的劲度系数k＝200 N/m，且弹簧始终在弹性限度内，空气阻力可忽略不计，重力加速度g取10 m/s².求：

(1)乙物体和甲物体碰撞过程中损失的动能；

(2)乙物体和甲物体碰撞后一起向下运动至最低点的过程中，乙物体和甲物体克服弹簧弹力所做的功．

[解析]　(1)设乙物体和甲物体碰撞前瞬间乙物体的速度大小为v₁，

根据v＝2gh

解得v₁＝2 m/s＝2.8 m/s(说明：结果为2 m/s同样得分)

设乙物体和甲物体碰撞后的共同速度大小为v₂，由动量守恒定律有mv₁＝2mv₂

解得v₂＝v₁＝ m/s＝1.4 m/s(说明：结果为 m/s同样得分)

所以碰撞后系统的动能E_k2＝(2m)v＝2 J

因为甲、乙物体构成的系统碰撞前的动能E_k1＝4 J，所以乙物体和甲物体碰撞过程中损失的机械能

ΔE＝E_k1－E_k2＝2 J

(2)设甲物体静止时弹簧压缩量为x₁，根据平衡条件，

解得x₁＝＝5.0 cm

甲和乙碰撞后做简谐运动，在通过平衡位置时两物体所受合力为零，速度最大，设此时弹簧压缩量为x₂，

解得x₂＝＝10 cm

甲物体和乙物体一同上升到最高点，两物体与简谐运动平衡位置的距离，即简谐运动的振幅

A＝x₂+(H－x₁)＝15 cm

根据简谐运动的对称性可知，两物体向下运动的距离

x＝A+(x₂－x₁)＝20 cm

设两物体向下运动至最低点的过程中，克服弹簧弹力做功为W，

根据动能定理有 2mgx－W＝0－× 2mv　解得　W＝6.0 J

[答案]　(1)2 J　(2)6.0 J

15.

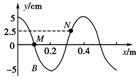
(12分)如右图所示为一列简谐波在t₁＝0时刻的图象．此时波中质点M的运动方向沿y轴负方向，且t₂＝0.55 s时质点M恰好第3次到达y轴正方向最大位移处．试求：

(1)此波沿什么方向传播？

(2)波速是多大？

(3)从t₁＝0至t₃＝1.2 s，质点N运动的路程和相对于平衡位置的位移分别是多少？

[解析]　(1)此波沿x轴负方向传播．

(2)在t₁＝0到t₂＝0.55 s这段时间时，质点M恰好第3次到达沿y轴正方向的最大位移处，则有：

(2+)T＝0.55 s，得T＝0.2 s

由图象得简谐波的波长为λ＝0.4 m，则波速

v＝＝2 m/s.

(3)在t₁＝0至t₃＝1.2 s这段时间，波中质点N经过了6个周期，即质点N回到始点，所以走过的路程为

s＝6×5×4 cm＝120 cm

相对于平衡位置的位移为2.5 cm.

[答案]　(1)沿x轴负方向　(2)2 m/s

(3)120 cm　2.5 cm