
题目列表(包括答案和解析)
7.

如右图所示水平圆盘绕中心坚直轴OO′匀速转动,在圆盘上沿半径方向放置两个完全相同的小物体A和B,小物体间用平行于圆盘的细线连接,两小物体随圆盘一起匀速转动.下列说法正确的是( )
A.细线中的张力可能为零
B.物体A受到的摩擦力一定指向圆心
C.物体B的线速度一定大于物体A的线速度
D.物体A的向心加速度大于物体B的向心加速度
[答案] ABC
6.如右图所示,质量为m的物块从半径为R的半球形碗边向碗底滑动,滑到最低点时的速度为v,若物块滑到最低点时受到的摩擦力是Ff,则物块与碗的动摩擦因数为( )
A. B.
C. D.
[解析] 物块滑到最低点时受竖直方向的重力、支持力和水平方向的摩擦力三个力作用,据牛顿第二定律FN-mg=m,又Ff=μFN,联立解得μ=,选项B正确.
[答案] B
5.地球和木星绕太阳运行的轨道都可以看做是圆形的.已知木星的轨道半径约为地球轨道半径的5.2倍,则木星与地球绕太阳运行的线速度之比约为( )
A.0.19 B.0.44
C.2.3 D.5.2
[解析] 根据公式=m可得到线速度与轨道半径之间的关系:=.
[答案] B
4.据报道,2009年4月29日,美国亚利桑那州一天文观测机构发现一颗与太阳系其他行星逆向运行的小行星,代号为2009HC82.该小行星绕太阳一周的时间为3.39年,直径2-3千米,其轨道平面与地球轨道平面呈155°的倾斜.假定该小行星与地球均以太阳为中心做匀速圆周运动,则小行星和地球绕太阳运动的速度大小的比值为( )
A.3.39- B.3.39-
C.3.39 D.3.39
[解析] 天体绕太阳做匀速圆周运动,由万有引力公式:
G=mr
又因为v=得v=2π=
所以v小∶v地=3.39-.
[答案] A
3.
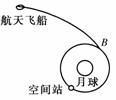
我国未来将建立月球基地,并在绕月轨道上建造空间站.如右图,关闭动力的航天飞机在月球引力作用下经椭圆轨道向月球靠近,并将与空间站B处对接.已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( )
A.图中航天飞机在飞向B处的过程中,月球引力做正功
B.航天飞机在B处由椭圆轨道可直接进入空间站轨道
C.根据题中条件可以算出月球质量
D.根据题中条件可以算出空间站受到月球引力的大小
[解析] 航天飞机在飞向B处的过程中,飞机受到的引力方向和飞行方向之间的夹角是锐角,月球引力做正功.由运动的可逆性知,航天飞机在B处先减速才能由椭圆轨道进入空间站轨道.由绕月球飞行的空间站m,=mr,可以算出月球质量M.空间站的质量不知,不能算出空间站受到的月球引力大小.故选项A、C正确.
[答案] AC
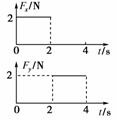
2.在一个光滑水平面内建立平面直角坐标系xOy,质量为1 kg的物体原来静止在坐标原点O(0,0),从t=0时刻起受到如右图所示随时间变化的外力作用,Fy表示沿y轴方向的外力,Fx表示沿x轴方向的外力,下列说法中正确的是( )
A.前2 s内物体沿x轴做匀加速直线运动
B.后2 s内物体继续做匀加速直线运动,但加速度沿y轴方向
C.4 s末物体坐标为(4 m,4 m)
D.4 s末物体坐标为(12 m,4 m)
[解析] 前2 s内物体只受x轴方向的作用力,故沿x轴做匀加速直线运动,A正确;其加速度为ax=2 m/s2,位移为x1=axt2=4 m.后2 s内物体沿x轴方向做匀速直线运动,位移x1=8 m,沿y轴方向做匀加速直线运动,加速度为ay=2 m/s2,位移为y=ayt2=4 m,故4 s末物体坐标为(12 m,4 m),D正确.
[答案] AD
1.如右图所示,汽车车厢顶部悬挂一个轻质弹簧,弹簧下端拴一个质量为m的小球,当汽车以某一速率在水平地面上匀速行驶时弹簧长度为L1;当汽车以同一速度匀速率通过一个桥面为圆弧形凸形桥的最高点时弹簧长度为L2,下列答案中正确的是( )
A.L1=L2 B.L1>L2
C.L1<L2 D.前三种情况均有可能
[答案] B
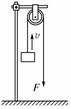
16.(12分)如下图所示,某同学用轻绳通过定滑轮提升一重物,运用传感器(未在图中画出)测得此过程中同时刻被提升重物的速度v与对轻绳的拉力F,并描绘出v-图象.假设某次实验所得的图象如图所示,其中线段AB与v轴平行,它反映了被提升重物在第一个时间段内v和的关系;线段BC的延长线过原点,它反映了被提升重物在第二个时间段内v和的关系;第三个时间段内拉力F和速度v均为C点所对应的大小保持不变,因此图象上没有反映.实验中还测得重物由静止开始经过t=1.4 s,速度增加到vc=3.0 m/s,此后物体做匀速运动.取重力加速度g=10 m/s2,绳重及一切摩擦和阻力均可忽略不计.
(1)在提升重物的过程中,除了重物的质量和所受重力保持不变以外,在第一个时间段内和第二个时间段内还各有一些物理量的值保持不变.请分别指出第一个时间段内和第二个时间段内所有其他保持不变的物理量,并求出它们的大小;
(2)求被提升重物在第一个时间段内和第二个时间段内通过的总路程.
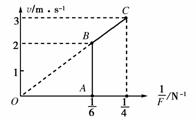
[解析] 由v-图象可知,第一时间段内重物所受拉力保持不变,且F1=6.0 N…
因第一时间段内重物所受拉力保持不变,所以其加速度也保持不变,设其大小为a,
根据牛顿第二定律有F1-G=ma,
重物速度达到vc=3.0 m/s时,受平衡力,即G=F2=4.0 N,
由此解得重物的质量m==0.40 kg
联立解得a=5.0 m/s2
在第二段时间内,拉力的功率保持不变P=Fv=12 W
(2)设第一段时间为t1,重物在这段时间内的位移为x1,则
t1== s=0.40 s,x1=at=0.40 m
设第二段时间为t2,t2=t-t1=1.0 s
重物在t2这段时间内的位移为x2,根据动能定理有Pt2-Gx2=mv-mv解得x2=2.75 m
所以被提升重物在第一时间段内和第二时间段内通过的总路程x=x1+x2=3.15 m.
[答案] (1)第一时间段内重物所受拉力保持不变,6.0 N;在第二段时间内,拉力的功率保持不变12 W
(2)3.15
15.(12分)
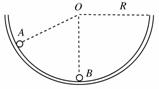
如右图,半径为R的光滑圆形轨道固定在竖直面内.小球A、B质量分别为m、3m.A球从左边某高处由静止释放,并与静止于A轨道最低点的B球相撞,碰撞后A球被反向弹回,且A、B球能达到的最大高度均为R.重力加速度为g.试求:
(1)碰撞刚结束时B球对轨道的压力大小;
(2)通过计算说明,碰撞过程中,A、B球组成的系统有无机械能损失?若有损失,求出损失了多少?
[解析] (1)因A、B球能达到的最大高度均为R,由机械能守恒定律,得到碰撞后小球的速度大小为:
mv2=mgR, vA=vB=,
设B球受到的支持力大小为FN,根据牛顿第二定律:FN-3mg=3m,得FN=mg.
由牛顿第三定律,小球B对轨道的压力大小为:F′N=FN=mg.
(2)设A球碰前的速度方向为正方向,碰撞过程满足动量守恒定律,
mv0=-mvA+3mvB
代入vA与vB的值,有:v0=
碰前系统的机械能E1=mv-mgR,
碰后系统的机械能为E2=mgR+3mgR=mgR,
故,E1=E2,无机械能损失.
[答案] (1)mg (2)无机械能损失
14.(12分)

如右图所示,水平传送带正以2 m/s的速度运行,两端水平距离l=8 m,把一质量m=2 kg的一个物块轻轻放到传送带的A端,物块在传送带的带动下向右运动,若物块与传送带间的动摩擦因数μ=0.1,则把这个物块从A端传送到B端的过程中,不计物块的大小,g取10 m/s2,求:
(1)摩擦力做功的平均功率;
(2)摩擦力做功的最大功率.
[解析] 物体刚放到传送带上时,由于与传送带有相对运动,物块受向右的滑动摩擦力,物块做加速运动,摩擦力对物块做功,求出物块在摩擦力作用下的位移和运动时间,由P=和P=Fv分别求出平均功率和最大功率.
(1)物块受向右的摩擦力为:
Ff=μmg=0.1×2×10 N=2 N
加速度为
a==μg=0.1×10 m/s2=1 m/s2
当物块与传送带相对静止时的位移为:
s== m=2 m.
摩擦力做功为:W=Ffs=2×2 J=4 J
相对静止后物块与传送带之间无摩擦力,此后物块匀速运动到B端,物块由A端到B端所用的时间为:
t=+= s+ s=5 s
则物块在被传送过程中所受摩擦力的平均功率为:
== W=0.8 W
(2)当物块在传送带上加速到与传送带速度相同时,摩擦力的功率最大,则
Pm=Ffv=2×2 W=4 W.
[答案] (1)0.8 W (2)4 W
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com