
题目列表(包括答案和解析)
11.
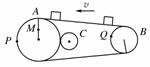
如右图所示为生产流水线上的皮带传输装置,传送带上等间距地放着很多半成品.A处装有光电计数器,它可以记录通过A处产品的数目.已知测得A、B的半径分别为rA=20 cm,rB=10 cm,相邻两产品距离为30 cm,每分钟内均有40个产品通过A处.求:
(1)产品随传送带移动的速度大小;
(2)A、B轮缘上的两点P、Q及A轮半径中点M的线速度大小;
(3)如果A轮是通过摩擦带动C轮转动,且rC=5 cm,求出C轮的角速度(假设轮不打滑).
[解析] (1)产品随传送带移动的速度
v== m/s=0.2 m/s.
(2)A、B轮缘上的两点P、Q的线速度vP=vQ=0.2 m/s,
M、P点的角速度相等:ωM=ωP==1 rad/s
因此半径中点M的线速度vM=vP=0.1 m/s.
(3)C轮的角速度ωC===4 rad/s.
[答案] (1)0.2 m/s (2)0.2 m/s 0.2 m/s 0.1 m/s
(3)4 rad/s
10.
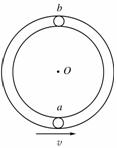
(2010年长沙五校联考)如右图所示光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
A.当小球b在最高点对轨道无压力时,小球a比小球b所需向心力大5 mg
B.当v=时,小球b在轨道最高点对轨道无压力
C.速度v至少为,才能使两球在管内做圆周运动
D.只要v≥,小球a对轨道最低点的压力比小球b对轨道最高点的压力都大6 mg
[解析] 小球在最高点恰好对轨道没有压力时,小球b所受重力充当向心力,mg=m⇒v0=,小球从最高点运动到最低点过程中,只有重力做功,小球的机械能守恒,2mgR+mv=mv2,解以上两式可得:v=,B项正确;小球在最低点时,F向=m=5mg,在最高点和最低点所需向心力的差为4 mg,A项错;小球在最高点,内管对小球的支持力可以提供向心力,所以小球通过最高点的最小速度为零,再由机械能守恒定律可知,2mgR=mv′2,解得v′=2,C项错;当v≥时,小球在最低点所受支持力F1=mg+,由最低点运动到最高点,2mgR+mv=mv2,轨道对小球的力F2+mg=m,解得F2=m-5mg,F1-F2=6mg,可见小球a对轨道最低点压力比小球b对轨道最高点压力都大6mg,D项正确.
[答案] BD
9.如图所示,A、B是两只相同的齿轮,A被固定不能转动,若B齿轮绕A齿轮运动半周,到达图中的C位置,则B齿轮上所标出的竖直向上的箭头所指的方向是( )

A.竖直向上 B.竖直向下
C.水平向左 D.水平向右
[解析] 在B齿轮绕A齿轮转动的同时,B齿轮上的各点也同时绕B齿轮的圆心运动.因为B齿轮绕A齿轮公转半径是B齿轮边缘上各点绕B齿轮圆心自转半径的2倍,所以当B齿轮绕A齿轮转半圈时,B齿轮上箭头所在点自转了一周,箭头仍竖直向上.
[答案] A
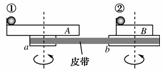
8.(2010年汕头模拟)如下图,在验证向心力公式的实验中,质量相同的钢球①放在A盘的边缘,钢球②放在B盘的边缘,A、B两盘的半径之比为2∶1.a、b分别是与A盘、B盘同轴的轮.a轮、b轮半径之比为1∶2.当a、b两轮在同一皮带带动下匀速转动时,钢球①②受到的向心力之比为( )
A.2∶1 B.4∶1
C.1∶4 D.8∶1
[解析] a、b两轮在同一皮带带动下匀速转动,说明a、b两轮的线速度相等,即va=vb,又因a轮与A盘同轴,b轮与B盘同轴,对应的角速度相等,再利用向心力公式得D项正确.
[答案] D
7.
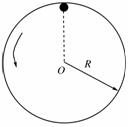
(2010年陕西省西安市统测)如右图所示,质量为m的小球在竖直平面内的光滑圆环轨道上做圆周运动.圆环半径为R,小球经过圆环最高点时刚好不脱离圆环,则其通过最高点时( )
A.小球对圆环的压力大小等于mg
B.小球受到的向心力等于0
C.小球的线速度大小等于
D.小球的向心加速度大小等于g
[解析] 小球在最高点时刚好不脱离圆环,则圆环刚好对小球没有作用力,小球只受重力,重力竖直向下,过圆心,根据牛顿第二定律得小球的向心加速度大小为a==g,再根据圆周运动规律得a==g,解得v=.
[答案] CD
6.(2010年湖南省长沙市调研)一宇航员到达半径为R、密度均匀的某星球表面,做如下实验:用不可伸长的轻绳拴一质量为m的小球,上端固定在O点,如下图甲所示,在最低点给小球某一初速度,使其绕O点在竖直面内做圆周运动,测得绳的拉力大小F随时间t的变化规律如下图乙所示.F1=7 F2,设R、m、引力常量为G以及F1为已知量,忽略各种阻力.以下说法正确的是( )

A.该星球表面的重力加速度为
B.卫星绕该星球的第一宇宙速度为
C.星球的质量为
D.小球在最高点的最小速度为零
[解析] 小球在最低点有F1-mg=m;小球在最高点有F2+mg=m;小球从最低点到最高点的过程中遵循机械能守恒定律mv=mg2R+mv,又F1=7F2,联立解得该星球表面的重力加速度为g=,选项A正确;由G=m得卫星绕该星球的第一宇宙速度为,选项B错误;由G=mg和g=解得星球的质量为,选项C正确.
[答案] AC
5.

如右图所示,半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球,现给小球一个冲击使其在瞬间得到一个水平初速度v0,若v0大小不同,则小球能够上升到的最大高度(距离底部)也不同.下列说法中正确的是( )
A.如果v0=,则小球能够上升的最大高度为
B.如果v0=,则小球能够上升的最大高度为
C.如果v0=,则小球能够上升的最大高度为
D.如果v0=,则小球能够上升的最大高度为2R
[解析] 根据机械能守恒定律,当速度为v0=,由mgh=mv解出h=,A项正确,B项错误;当v0=,小球正好运动到最高点,D项正确;当v0=时小球运动到最高点以下,若C项成立,说明小球此时向心力为0,这是不可能的.
[答案] AD
4.
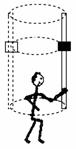
如右图所示,某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动,将螺丝帽套在塑料管上,手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动,则只要运动角速度合适,螺丝帽恰好不下滑,假设螺丝帽与塑料管间的动摩擦因数为μ,认为最大静摩擦力近似等于滑动摩擦力.则在该同学手转塑料管使螺丝帽恰好不下滑时,下述分析正确的是( )
A.螺丝帽受的重力与最大静摩擦力平衡
B.螺丝帽受到杆的弹力方向水平向外,背离圆心
C.此时手转动塑料管的角速度ω=
D.若杆的转动加快,螺丝帽有可能相对杆发生运动
[解析] 由于螺丝帽做圆周运动过程中恰好不下滑,则竖直方向上重力与摩擦力平衡,杆对螺丝帽的弹力提供其做匀速圆周运动的向心力,选项A正确、B、C错误;无论杆的转动速度增大多少,竖直方向受力平衡,故选项D错误.
[答案] A
3.火车以某一速度v通过某弯道时,内、外轨道均不受侧压力作用,下面分析正确的是( )
A.轨道半径R=
B.若火车速度大于v时,外轨将受到侧压力作用,其方向平行于轨道平面向外
C.若火车速度小于v时,外轨将受到侧压力作用,其方向平行于轨道平面向内
D.当火车质量改变时,安全速率也将改变
[解析] 当内、外轨道均不受侧压力作用时,重力和支持力的合力提供向心力,mgtan θ=,可看出安全速率与质量无关,A、D错误;火车速度大于v时,外轨将受到侧压力作用,若火车速度小于v时,内轨将受到侧压力作用.
[答案] B
2.
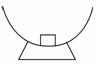
如右图所示,质量为m的物体从半径为R的半球形碗边向碗底滑动,滑到最低点时的速度为v,若物体与碗的动摩擦因数为μ,则物体滑到最低点时受到的摩擦力是( )
A.μmg B.μm
C.μm D.μm
[解析] 物体滑到最低点时受到的摩擦力Ff=μFN,FN-mg=mv2/R,联立解得:Ff=μm(g+v2/R),故B对.
[答案] B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com