13．如图所示，一个厚度不计的圆环A，紧套在长度为L的圆柱体B的上端，A、B两者的质量均为m，A与B之间的最大静摩擦力与滑动摩擦力相同，其大小为kmg(k>1)．B在离地H高处由静止开始落下，触地后能竖直向上弹起，触地时间极短，且无动能损失，B与地碰撞若干次后A与B分离．求：

(1)B与地第一次碰撞后，经多长时间A与B达到相同的速度；

(2)当A与B第一次达到相同速度时，B下端离地面的高度是多少．

[答案]　(1)　(2)H

[解析]　(1)B与地第一次碰撞后，以v₀＝向上运动，加速度a_B＝(k+1)g，方向向下；

此时刻A以速度v₀＝向下运动，加速度a_A＝(k－1)g，方向向上．

取向下为正方向，设A、B共同速度为v₁，

对A有：v₁＝v₀－(k－1)gt，

对B有：v₁＝－v₀+(k+1)gt

解得t＝

(2)由以上各式解得，A与B第一次达到的相同速度v₁＝，方向向下．

解法一　B下端离地面的高度h＝v₀t－＝H.

解法二　用平均速度求解：h＝t＝H.

解法三　用动能定理：对B，－(mg+kmg)h＝mv－mv，解得h＝H.

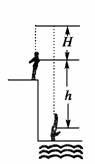
12．跳伞运动员做低空跳伞表演，当飞机在离地面224m高处水平飞行时，运动员离开飞机在竖直方向做自由落体运动，运动一段时间后，立即打开降落伞，展伞后运动员以12.5m/s²的平均加速度匀减速下降，为了运动员的安全，要求运动员落地速度最大不得超过5m/s.g＝10m/s²，求：

(1)运动员展伞时离地的高度至少为多少？着地时相当于从多高处自由落下？

(2)运动员在空中的最短时间为多少？

[答案]　(1)99m,1.25m　(2)8.6s

[解析]　设展伞时跳伞员的速度为v₀.距地面的高度为h，到达地面速度为v_地．据题意得：

224m－h＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

v－v＝－2ah　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

联立①②得：h＝99m，v₀＝50m/s.

设实际相当于h′高度跳下

则2gh′＝v　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

解h′＝1.25m

当跳伞员恰好以5m/s的速度落地时间最短，设时间为t，自由下落时间为t₁，减速运动时间为t₂，据题意：

t＝t₁+t₂ ④

v₀＝gt₁ ⑤

t₂＝h　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑥

联立第(1)问和④⑤⑥式得

t＝8.6s.

0.8v)²＝2as′，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

由s＝25m，解得s′＝16m.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

(2)设乙应在距离甲s₀处起跑，由几何关系得

s′+s₀＝vt.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ④

s′＝t＝0.4vt，　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑤

由③④⑤得s₀＝24m.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑥

11．甲、乙两个同学在直跑道上进行4×100m接力(如图所示)，他们在奔跑时有相同的最大速度，乙从静止开始全力奔跑需跑出25m才能达到最大速度，这一过程可看作匀加速直线运动．现在甲持棒以最大速度向乙奔来，乙在接力区伺机全力奔出．若要求乙接棒时奔跑的速度达到最大速度的80%，则：

(1)乙在接力区须奔出多少距离？

(2)乙应在距离甲多远时起跑？

[答案]　(1)16m　(2)24m

[解析]　对于此类问题，关键在于正确分析两物体的运动性质以及物体的运动时间、位移和速度的关系．

(1)乙在接力区做初速度为零的匀加速运动．设乙的加速度为a，速度为0.8v时位移为s′，v²＝2as，　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

10．在北京奥运会上，一跳水运动员从离水面10m高的平台上向上跃起，举双臂直体离开台面，此时重心位于从手到脚全长的中点，跃起后重心升高0.45m达到最高点，落水时身体竖直，手先入水，从离开平台到手接触水面，运动员可以用于完成动作的时间为________s，在此过程中，运动员水平方向的运动忽略不计，运动员可视作全部质量集中在重心的一个质点，取g＝10m/s²

[答案]　1.7s

[解析]　如图所示，从平台跃起，到手接触水面，运动员重心的高度变化为h＝10m

解法一　将整个过程分上升和下降两个阶段考虑，设运动员跃起的初速度为v₀，则＝H

v₀＝＝＝3(m/s)

故上升时间为：t₁＝＝0.3(s)

设运动员从最高点到手接触水面所用时间为t₂，则：gt＝h+H

t₂＝＝＝1.4(s)

故用于完成动作的时间t为

t＝t₁+t₂＝1.7(s)

综上所述，本题正确的答案为1.7s

解法二　运动员的整个运动过程为竖直上抛运动，设总时间为t，由于运动员入水时位于跃起位置下方10m处，故该过程中位移为x＝－h，即：

x＝v₀t－gt²＝－h

其中v₀＝3m/s

代入数据得：5t²－t－10＝0

t＝＝1.7(s)(另一根舍去)

9．利用水滴下落可以测量重力加速度g，调节水龙头，让水一滴一滴地流出，在水龙头的正下方放一盘子，调整盘子的高度，使一滴水滴碰到盘子时，恰好有另一滴水从水龙头开始下落，而空中还有两个正在下落的水滴，测出水龙头处到盘子的高度为h(m)，再用秒表测量时间，从第一滴水离开水龙头开始，到第N滴水落至盘中，共用时间为T(s)，当第一滴水落到盘子时，第二滴水离盘子的高度为________m，重力加速度g＝________m/s².

[答案]　h　2(N+2)²h/9T²

[解析]　因为任意两滴水之间的时间间隔相等，设任意两滴水之间的时间间隔为t，第一滴水下落的时间为3t，则有

h＝g(3t)²

第一滴水落到盘子时，第二滴水下落的时间为2t

则第二滴水离盘子的高度为

h′＝h－g(2t)²＝h－h＝h

又(N+2)t＝T

故g＝＝2(N+2)²h/9T²

8．(2009·浙江余姚中学质检)正在匀加速沿平直轨道行驶的长为L的列车，保持加速度不变通过长度为L的桥．车头驶上桥时的速度为v₁，车头经过桥尾时的速度为v₂，则列车过完桥时的速度为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　 D.

[答案]　D

[解析]　列车过完桥行驶的距离为2L，车头经过桥尾时的速度为v₂刚好是这一段距离的中间位置，设列车过完桥时的速度为v，则v₂＝，解得v＝.

7．一物体从高x处做自由落体运动，经时间t到达地面，落地速度为v，那么当物体下落时间为时，物体的速度和距地面的高度分别是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.，　 　　　　　　　　　　　　　　　　　　　　　　　　 B.，

C.，x　 　　　　　　　　　　　　　　　　　　　　 D.，x

[答案]　C

[解析]　根据运动学公式v＝gt得，速度v与时间t成正比，所以下落时的速度为

v′＝v·＝.

根据公式x＝gt²得，下落位移h与时间的平方t²成正比，所以下落时下落的高度为

x′＝x·＝x.

所以距地面高度x_距＝x－x′＝x－x＝x.

6．两辆完全相同的汽车，沿平直公路一前一后匀速行驶，速度均为v₀，若前车突然以恒定加速度刹车，在它刚停住时，后车以前车刹车时的加速度开始刹车，已知前车在刹车过程中所行距离为s，若要保证两辆车在上述情况中不相撞，则两车在匀速行驶时保持的距离至少应为：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．s　 　　　　　　　　　　　　　　　　　　　　　　 B．2s

C．3s　 　　　　　　　　　　　　　　　　　　　　　　 D．4s

[答案]　B

[解析]　设两车行进中保持距离为Δx，则有

v₀t+≤s+Δx　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (1)

又t＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (2)

s＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (3)

联立得Δx≥2s，B对．

5．如图所示，在水平面上固定着三个完全相同的木块，一子弹以水平速度v射入木块，若子弹在木块中做匀减速直线运动，当穿透第三个木块时速度恰好为零，则子弹依次射入每个木块时的速度比和穿过每个木块所用的时间比分别为　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．v₁:v₂:v₃＝3:2:1

B．v₁:v₂:v₃＝::1

C．t₁:t₂:t₃＝1::

D．t₁:t₂:t₃＝(－):(－1):1

[答案]　D

[解析]　用“逆向思维”法解答．由题知，若倒过来分析，子弹向左做匀加速直线运动，初速度为零，设每块木块长为L，则v＝2a·L，v＝2a·2L，v＝2a·3L，v₃、v₂、v₁分别为子弹倒过来向左穿透第3块木块后、穿透第2块木块后、穿透第1块木块后的速度，则v₁:v₂:v₃＝::1.子弹依次向右穿入每个木块时速度比v₁:v₂:v₃＝::1，因此选项A、B错．由v₃＝at₃，v₂＝a(t₂+t₃)，v₁＝a(t₁+t₂+t₃)．三式联立，得t₁:t₂:t₃＝(－):(－1):1，因此选项D对．