2．(2010·湖南省师大附中月考)一带电粒子以初速度v₀沿垂直于电场线和磁感线的方向，先后穿过宽度相同且紧邻在一起的有明显边界的匀强电场(场强为E)和匀强磁场(磁感应强度为B)，如图甲所示．电场和磁场对粒子做功为W₁，粒子穿出磁场时的速度为v₁；若把电场和磁场正交叠加，如图乙所示，该粒子仍以初速度v₀穿过叠加场区，电场和磁场对粒子做功为W₂，粒子穿出场区时的速度为v₂，比较W₁和W₂、v₁和v₂的大小(v₀<E/B，不计重力)　　　 　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)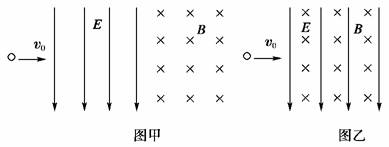

A．W₁>W₂，v₁>v₂　　B．W₁＝W₂，v₁＝v₂

C．W₁<W₂，v₁<v₂　 　　　　　 D．W₁＝W₂，v₁>v₂

[答案]　A

[解析]　由于v₀<E/B，电场力>洛伦兹力，则第一种情况下，粒子沿电场方向的位移较大，电场力做功较多，出射速度较大，A对．

1．如图所示，MN是纸面内的一条直线，其所在空间充满与纸面平行的匀强电场或与纸面垂直的匀强磁场(场区都足够大)，现有一重力不计的带电粒子从MN上的O点以水平初速度v₀射入场区，下列有关判断正确的是　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

A．如果粒子回到MN上时速度增大，则空间存在的一定是电场

B．如果粒子回到MN上时速度大小不变，则该空间存在的一定是电场

C．若只改变粒子的速度大小，发现粒子再回到MN上时与其所成夹角不变，则该空间存在的一定是磁场

D．若只改变粒子的速度大小，发现粒子再回到MN所用的时间不变，则该空间存在的一定是磁场

[答案]　AD

[解析]　洛伦兹力对带电粒子不做功，不能使粒子速度增大，电场力可使带电粒子做功，动能增大，故A项正确．若带电粒子以与电场线平行的速度v₀射入，粒子返回速率不变，故B、C项错．由T＝知，粒子在磁场中运动的时间与速率无关，故D项正确．

12．飞行时间质谱仪可以对气体分子进行分析．如图所示，在真空状态下，脉冲阀P喷出微量气体，经激光照射产生不同价位的正离子，自a板小孔进入a、b间的加速电场，从b板小孔射出，沿中线方向进入M、N板间的偏转控制区，到达探测器．已知元电荷电量为e、a、b板间距为d，极板M、N的长度和间距均为L.不计离子重力及进入a板时的初速度．

(1)当a、b间的电压为U₁时，在M、N间加上适当的

电压U₂，使离子到达探测器．请导出离子的全部飞行时间与比荷K(K＝ne/m)的关系式．

(2)去掉偏转电压U₂，在M、N间区域加上垂直于纸面的匀强磁场，磁感应强度为B，若进入a、b间所有离子质量均为m，要使所有的离子能通过控制区从右侧飞出，a、b间的加速电压U₁至少为多少？

[答案]　(1)t＝　(2)

[解析]　(1)由动能定理：neU₁＝mv²

n价正离子在a、b间的加速度：a₁＝

在a、b间运动的时间：t₁＝＝d

在M、N间运动的时间：t₂＝＝L

离子到达探测器的时间：t＝t₁+t₂＝.

(2)假定n价正离子在磁场中向N板偏转，洛伦兹力充当向心力，设轨迹半径为R，由牛顿第二定律得：nevB＝m

离子刚好从N板右侧边缘穿出时，由几何关系得：

R²＝L²+(R－L/2)²

由以上各式得：U₁＝

当n＝1时U₁取最小值U_min＝.

11．如右图所示为一种可用于测量电子电荷量e与质量m比值e/m的阴极射线管，管内处于真空状态，图中L是灯丝，当接上电源时可发出电子，A是中央有小圆孔的金属板，当L和A间加上电压时(其电压值比灯丝电压大得多)，电子将被加速并沿图中虚直线所示的路径到达荧光屏S上的O点，发出荧光．P₁、P₂为两块平行于虚直线的金属板，已知两板间距为d，在虚线所示的圆形区域内可施加一匀强磁场，已知其磁感应强度为B，方向垂直纸面向外．a、b₁、b₂、c₁、c₂都是固定在管壳上的金属引线．E₁、E₂、E₃是三个电压可调并可读出其电压值的直流电源．

(1)试在图中画出三个电源与阴极射线管的有关引线的连线．

(2)导出计算e/m的表达式，要求用所测物理量及题给出已知量表示．

[答案]　(1)略　(2)

[解析]　(1)各电源的连线如右图所示

(2)设加速电压U₂，电子加速后穿过小孔的速度为v，则有

mv²＝eU₂①

施加磁场后，要使电子仍打在O点，应在P₁、P₂之间加上适当的电压U₃，使电子所受的电场力和洛伦兹力平衡，有e＝eBv②

由①、②两式可解得＝.

10．(2009·合肥市一模)质谱仪可测定同位素的组成．现有一束一价的钾39和钾41离子经电场加速后，沿着与磁场和边界均垂直的方向进入匀强磁场中，如图所示．测试时规定加速电压大小为U₀，但在实验过程中加速电压有较小的波动，可能偏大或偏小ΔU.为使钾39和钾41打在照相底片上的区域不重叠，ΔU不得超过多少？(不计离子的重力)

[答案]　U₀

[解析]　设加速电压为U，磁场的磁感应强度为B，电荷的电荷量为q、质量为m，运动半径为R，则

由qU＝mv²　qvB＝m解得R＝

由此式可知，在B、q、U相同时，m小的半径小，所以钾39半径小，钾41半径大；在m相同时，U大半径大．

设：钾39质量为m₁，电压为U₀+ΔU时，最大半径为R₁；钾41质量为m₂；电压为U₀－ΔU时，钾41最小半径为R₂.则

R₁＝

R₂＝

令R₁＝R₂，则m₁(U₀+ΔU)＝m₂(U₀－ΔU)

解得：ΔU＝U₀＝U₀＝U₀.

9．串联加速器是用来产生高能离子的装置．如图线框内为其主体的原理示意图，其中加速管的中部b处有很高的正电势U.a、c两端均有电极接地(电势为零)．现将速度很低的负一价碳离子从a端输入，当离子到达b处时，可被设在b处的特殊装置将其电子剥离，成为n价正离子，而不改变其速度大小，这些正n价碳离子从c端飞出后进入一与其速度方向垂直的、磁感应强度为B的匀强磁场中，在磁场中做半径为R的圆周运动．已知碳离子的质量m＝2.0×10^－26kg，U＝7.5×10⁵V，B＝0.5T，n＝2，基元电荷e＝1.6×10^－19C，求R.

[答案]　0.75m

[解析]　设碳离子到达b处的速度为v₁，从c端射出的速度为v₂，由能量关系得mv＝eU，①

mv＝mv+neU，②

进入磁场后，碳离子做圆周运动，可得nev₂B＝，③

由以上三式得R＝ 代入数据得R＝0.75m.

8．有一回旋加速器，两个D形盒的半径为R，两D形盒之间的高频电压为U，偏转磁场的磁感应强度为B.如果一个α粒子(氦原子核)和一个质子，都从加速器的中心开始被加速，试求它们从D形盒飞出时的速度之比．

[答案]　1?2

[解析]　带电粒子在D形盒内做匀速圆周运动的向心力是由洛伦兹力提供的，对带电粒子飞出回旋加速器的最后半圆，根据第二定律有：qBv＝m，解得v＝BR.因为B、R为定值，所以带电粒子从D形盒飞出的速度与带电粒子的比荷成正比．因α粒子的质量是质子的4倍，α粒子的电荷量是质子的2倍，故＝.

7．竖直放置的半圆形光滑绝缘管道处在如图所示的匀强磁场中，B＝1.1T，管道半径R＝0.8m，其直径POQ在竖直线上，在管口P处以2m/s的速度水平射入一个带电小球(可视为质点)，其电荷量为10^－4C(g取10m/s²)，小球滑到Q处时的速度大小为________；若小球从Q处滑出瞬间，管道对它的弹力正好为零，小球的质量为________．

[答案]　6m/s　1.2×10^－5kg

[解析]　小球在管道中受重力、洛伦兹力和轨道的作用力，而只有重力对小球做功，由动能定理得：mg·2R＝mv－mv，解得v_Q＝＝6m/s.

在Q处弹力为零，则洛伦兹力和重力的合力提供向心力，有qv_QB－mg＝m·.

解得m＝1.2×10^－5kg.

6．图甲是用来加速带电粒子的回旋加速器的示意图，其核心部分是两个D形金属盒，在加速带电粒子时，两金属盒置于匀强磁场中，并分别与高频电源相连．带电粒子在运动中的动能E_k随时间t的变化规律如图乙所示．若忽略带电粒子在电场中的加速时间，则下列判断正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．从E_k－t图可知，要想粒子获得的最大动能越大，则要求D形盒的面积也越大

B．在E_k－t图中应有t₄－t₃＝t₃－t₂＝t₂－t₁

C．高频电源的变化周期应该等于t_n－t_n－1

D．从E_k－t图可知，粒子加速次数越多，粒子的最大动能一定越大

[答案]　AB

[解析]　由带电粒子在磁场中的周期T＝可知B正确；粒子运动一周的时间为2(t_n－t_n－1)，故C错；由R_m＝可知，带电粒子的最大动能与D形盒的半径有关，故D错误；A正确．

5．(2009·滨州)如图所示是质谱仪工作原理的示意图．带电粒子a、b经电压U加速(在A点的初速度为零)后，进入磁感应强度为B的匀强磁场做匀速圆周运动，最后分别打在感光板S上的x₁、x₂处．图中半圆形的虚线分别表示带电粒子a、b所通过的路径，则(　)

A．a的质量一定大于b的质量

B．a的电荷量一定大于b的电荷量

C．在磁场中a运动的时间大于b运动的时间

D．a的比荷大于b的比荷

[答案]　D

[解析]　设粒子经电场加速后的速度为v，由动能定理，有qU＝mv²，则粒子在磁场中做匀速圆周运动的半径R＝＝∝，由图知粒子a的轨迹半径小于粒子b的轨迹半径，故<，选项D正确，A、B错误；粒子在磁场中的运动时间t＝＝，结合上式，有t_a<t_b，选项C错误．