12．如图甲所示，水平地面上有一辆固定有竖直光滑绝缘管的小车，管的底部有一质量m＝0.2g、电荷量q＝8×10^－5C的小球，小球的直径比管的内径略小．在管口所在水平面MN的下方存在着垂直纸面向里、磁感应强度B₁＝15T的匀强磁场，MN面的上方还存在着竖直向上、场强E＝25V/m的匀强电场和垂直纸面向外、磁感应强度B₂＝5T的匀强磁场．现让小车始终保持v＝2m/s的速度匀速向右运动，以带电小球刚经过场的边界PQ为计时的起点，测得小球对管侧壁的弹力F_N随高度h变化的关系如图乙所示．g取10m/s²，不计空气阻力，求：

(1)小球刚进入磁场B₁时的加速度大小a；

(2)绝缘管的长度L；

(3)小球离开管后再次经过水平面MN时距管口的距离Δx.

[答案]　(1)2m/s²　(2)1m　(3)m

[解析]　(1)以小球为研究对象，竖直方向小球受重力和恒定的洛伦兹力f₁，故小球在管中竖直方向做匀加速直线运动，加速度设为a，设a＝＝＝2m/s².

(2)当小球运动到管口时，F_N＝2.4×10^－3N，

设v₁为小球竖直分速度，由F_N＝qv₁B₁，则v₁＝＝2m/s，

由v＝2aL得L＝＝1m.

(3)小球离开管口进入复合场，其中qE＝2×10^－3N，mg＝2×10^－3N.

故电场力与重力平衡，小球在复合场中做匀速圆周运动，合速度v′＝2m/s，

与MN成45°角，设轨道半径为R，

qB₂v′＝m，R＝＝m.

从小球离开管口开始计时，到再次经过MN所通过的水平距离x₁＝R＝2m.

对应时间t＝T＝＝s.

小车运动距离为x₂，x₂＝vt＝m.

此时，小球距离管口的距离是Δx＝x₁－x₂＝m.

11．如图甲所示，竖直面MN的左侧空间存在竖直向上的匀强电场(上、下及左侧无边界)．一个质量为m、电荷量为q的可视为质点的带正电的小球，以大小为v₀的速度垂直于竖直面MN向右做直线运动．小球在t＝0时刻通过电场中的P点，为使小球能在以后的运动中竖直向下通过D点(P、D间距为L，且它们的连线垂直于竖直平面MN，D到竖直面MN的距离DQ等于L/π)，经过研究，可以在电场所在的空间叠加如图乙所示的随时间周期性变化的、垂直于纸面向里的磁场．(g＝10m/s²)，求：

(1)场强E的大小；

(2)如果磁感应强度B₀为已知量，试推出满足条件t₁的表达式；

(3)进一步的研究表明，竖直向下的通过D点的小球将做周期性运动．则当小球运动的周期最大时，求出磁感应强度B₀及运动的最大周期T的大小，并在图中定性地画出小球运动一个周期的轨迹．(只需要画出一种可能的情况)

[答案]　(1)mg/q　(2)+　(3)　轨迹见解析图乙

[解析]　(1)小球进入电场，做匀速直线运动时

Eq＝mg，①

E＝mg/q.②

(2)在t₁时刻加磁场，小球在时间t₀内做匀速圆周运动(如图甲所示)，设圆周运动的周期为T₀，半径为R₀.

竖直向下通过D点，则t₀＝3T₀/4，　　　 ③

B₀qv₀＝m④

PF－PD＝R即v₀t₁－L＝R，　　　　　　 ⑤

将③④代入⑤式解得t₁＝+.

(3)小球运动的速率始终不变，当R变大时，T₀也增加，小球在电场中的运动周期T也增加

在小球不飞出电场的情况下，当T₀最大时，有：

DQ＝2R，即＝，　　　　　　　 ⑥

T₀＝＝，　　　　　　　　　　 ⑦

结合⑥⑦式是B₀＝，

T₀＝.

结合轨迹图可知，小球在电场中运动的最大周期T＝4×(+t₀)．

结合上式解得T＝.

所以小球在电场中运动一个周期的轨迹如图乙所示．

10．2008年9月25日中国“神舟七号”宇宙飞船顺利升空，9月27日，中国宇航员首次实现太空出舱．下一步我国将于2015年发射空间站，设该空间站体积很大，宇航员可以在里面进行多项体育活动，一宇航员在站内玩垒球(万有引力可以忽略不计)，上半侧为匀强电场，下半侧为匀强磁场，中间为分界面，电场与分界面垂直，磁场垂直纸面向里，电场强度为E＝100V/m，宇航员位于电场一侧距分界面为h＝3m的P点，PO垂直于分界面，D位于O点右侧，垒球质量为m＝0.1kg，带电量为q＝－0.05C，该宇航员从P点以初速度v₀＝10m/s平行于界面投出垒球，要使垒球第一次通过界面就击中D点，且能回到P点．求：

(1)OD之间的距离d.

(2)垒球从抛出第一次回到P点的时间t.(计算结果保留三位有效数字)

[答案]　(1)3.46m　(2)1.53s

[解析]　(1)设垒球在电场中运动的加速度为a，时间为t₁，有：

qE＝ma

h＝at

d＝v₀t₁

代入数据得：a＝50m/s²，t₁＝s，

d＝2m＝3.46m

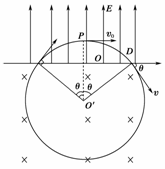(2)垒球进入磁场时与分界面夹角为θ

tanθ＝＝

θ＝60°

进入磁场时的速度为

v＝＝20m/s

设垒球在磁场中做匀速圆周运动的半径为R

由几何关系得：

R＝＝4m

又由R＝，得B＝＝10T

球在磁场中运动时间为：

t₂＝T

T＝，故t₂＝s

运动总时间为：

t＝2t₁+t₂＝1.53s

9．某空间区域存在匀强电场和匀强磁场，匀强电场的电场强度为0.5N/C，一带电量为q＝+10^－3C，质量为m＝3×10^－5kg的油滴从高5m处落入该区域后，恰好做匀速直线运动(忽略空气阻力的作用)，求匀强磁场的磁感应强度的最小值．(重力加速度g＝10m/s²)

[答案]　4×10^－2T

[解析]　带电油滴进入电场和磁场区域后做匀速直线运动，所以油滴处于受力平衡状态，油滴受力如右图所示．由于进入场区时速度竖直向下，所以磁场力F_洛一定在水平方向上，与重力垂直，所以电场力F在水平方向的分力等于磁场力F_洛，在竖直方向的分力等于重力G.

F＝qE＝0.5×10^－3N＝5×10^－4N①

mg＝3×10^－4N②

设F与竖直方向的夹角为θ，竖直方向上有：

mg＝Fcosθ③

水平方向上有：F_洛＝Fsinθ④

①②③④式可得：F_洛＝4×10^－4N

设油滴下落到场区时的速度为v，v＝＝10m/s

当速度与磁场垂直时，粒子所受的洛伦兹力最大．所以，当磁场与速度垂直时，磁场的磁感应强度最小，设磁感应强度的最小值为B.

F_洛＝qvB，B＝＝T＝4×10^－2T

8．(2009·皖南八校二模)如图所示，用一块金属板折成横截面为“”形的金属槽放置在磁感应强度为B的匀强磁场中，并以速率v₁向右匀速运动，从槽口右侧射入的带电微粒的速率是v₂，如果微粒进入槽后恰能做匀速圆周运动，则微粒做匀速圆周运动的轨道半径r和周期T分别为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.，　 　　　　　　　　　　　　　　　　 B.，

C.，　 　　　　　　　　　　　　　　　　　　 D.，

[答案]　B

[解析]　金属板折成“”形的金属槽放在磁感应强度为B的匀强磁场中，并以速率v₁向右匀速运动时，左板将切割磁感线，上、下两板间产生电势差，由右手定则可判断出上板为正，下板为负，E＝＝＝Bv₁，微粒做匀速圆周运动，重力等于电场力，方向相反，故有m＝＝，向心力由洛伦兹力提供，所以qv₂B＝m，得r＝＝，周期T＝＝，故B项正确．

7．如图所示，带电粒子以速度v₀从a点进入匀强磁场，运动中经过b点，Oa＝Ob，若撤去磁场加一个与y轴平行的匀强电场，仍以v₀从a点进入电场，粒子仍能通过b点，那么电场强度E与磁感应强度B之比为　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

A．v₀　 　　　　　　　　　　　　　　　　　　 B.

C．2v₀ 　　　　　　　　　　　　　　　　　　 D.

[答案]　C

[解析]　设Oa＝Ob＝d，因为带电粒子在磁场中做匀速圆周运动，所以圆周运动的半径正好等于d，即r＝＝d，得到B＝.如果换成匀强电场，水平方向以v₀做匀速直线运动，竖直沿y轴负方向做匀加速运动，即d＝×ײ，得到E＝，所以＝2v₀，选项C正确．

6．(2009·江苏省姜堰中学、淮阴中学、如皋中学、前黄中学模拟)如图所示，一粒子源位于一边长为a的正三角形ABC的中点O处，可以在三角形所在的平面内向各个方向发射出速度大小为v、质量为m、电荷量为q的带电粒子，整个三角形位于垂直于△ABC的匀强磁场中，若使任意方向射出的带电粒子均不能射出三角形区域，则磁感应强度的最小值为

(　)

A.　 　　　　　　　　　　　　　　　　　　　 B.

C. 　　　　　　　　　　　　　　　　　 　D.

[答案]　D

[解析]　如图所示带电粒子不能射出三角形区域的最小半径是r＝·tan30°＝a，由qvB＝m得，最小的磁感应强度是B＝.

5．在某地上空同时存在着匀强的电场与磁场，一质量为m的带正电小球，在该区域内沿水平方向向右做直线运动，如图所示，关于场的分布情况不可能的是　　　　　 (　)

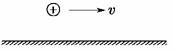A．该处电场方向和磁场方向重合

B．电场竖直向上，磁场垂直纸面向里

C．电场斜向里侧上方，磁场斜向外侧上方，均与v垂直

D．电场水平向右，磁场垂直纸面向里

[答案]　D

[解析]　带电小球在复合场中运动一定受重力和电场力，是否受洛伦兹力需具体分析．A选项中若电场、磁场方向与速度方向垂直，则洛伦兹力与电场力垂直，如果与重力的合力为0就会做直线运动．B选项中电场力、洛伦兹力都向上，若与重力合力为0，也会做直线运动．C选项中电场力斜向里侧上方，洛伦兹力向外侧下方，若与重力的合力为0，就会做直线运动．D选项三个力不可能为0，因此选项A、B、C正确，D错误．

4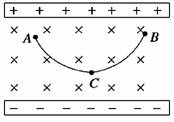．设空间存在竖直向下的匀强电场和垂直纸面向里的匀强磁场，如图所示，已知一离子在静电力和洛伦兹力的作用下，从静止开始自A点沿曲线ACB运动，到达B点时速度为零，C点是运动的最低点，忽略重力，下述说法中错误的是　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．该离子必带正电荷

B．A点和B点位于同一高度

C．离子在C点时速度最大

D．离子到达B点后，将沿原曲线返回A点

[答案]　D

[解析]　由离子从静止开始运动的方向可知离子带正电，因洛伦兹力不做功，只有静电力做功，由能量守恒或动能定理可知B、C正确，到达B后，将重复ACB过程，向右运动．

3．如图甲所示为一个质量为m、带电荷量为+q的圆环，可在水平放置的足够长的粗糙细杆上滑动，细杆处于磁感应强度为B的匀强磁场中．现给圆环向右的初速度v₀，在以后的运动过程中，圆环运动的速度-时间图象可能是图乙中的　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　 (　)

[答案]　AD

[解析]　由左手定则可判断洛伦兹力方向向上，圆环受到竖直向下的重力、垂直细杆的弹力及向左的摩擦力，当洛伦兹力初始时刻小于重力时，弹力方向竖直向上，圆环向右减速运动，随着速度减小，洛伦兹力减小，弹力越来越大，摩擦力越来越大，故做加速度增大的减速运动，直到速度为零而处于静止状态，选项中没有对应图象；当洛伦兹力初始时刻等于重力时，弹力为零，摩擦力为零，故圆环做匀速直线运动，A正确；当洛伦兹力初始时刻大于重力时，弹力方向竖直向下，圆环做减速运动，速度减小，洛伦兹力减小，弹力减小，当弹力减小到零的过程中，摩擦力逐渐减小到零，做加速度逐渐减小的减速运动，摩擦力为零时，开始做匀速直线运动，D正确．