
题目列表(包括答案和解析)
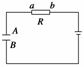
2.如图所示是一个由电池、电阻R与平行板电容器组成的串联电路.在增大电容器两极板间距离的过程中 ( )
 A.电阻R中没有电流
A.电阻R中没有电流
B.电容器的电容变小
C.电阻R中有从a流向b的电流
D.电阻R中有从b流向a的电流
[答案] BC
[解析] 由题意知,电容器两板间电压U一定,设已充电荷量为Q,当两板距离增大时,电容C变小,由Q=CU知Q减小,必有一部分正电荷通过电阻R回流.故BC对.
1.在平行板间加上如图所示周期性变化的电压,重力不计的带电粒子静止在平行板中央,从t=0时刻开始将其释放,运动过程无碰板情况,下列选项图中,能定性描述粒子运动的速度图象的是 ( )
[答案] A
[解析] 前带电粒子做匀加速直线运动,后做匀减速直线运动.T时刻速度减为零,以后重复第一周期内的运动,则正确答案为A.
17.(11分)(2009·福建质检)如图(甲)所示,水平放置的平行金属板A、B,两板的中央各有一小孔O1、O2,板间距离为d,开关S接1.当t=0时,在a、b两端加上如图(乙)所示的电压,同时在c、d两端加上如图(丙)所示的电压.此时,一质量为m的带负电微粒P恰好静止于两孔连线的中点处(P、O1、O2在同一竖直线上).重力加速度为g,不计空气阻力.
(1)若在t=时刻将开关S从1扳到2,当ucd=2U0时,求微粒P的加速度大小和方向;
(2)若要使微粒P以最大的动能从A板中的O1小孔射出,问在t=到t=T之间的哪个时刻,把开关S从1扳到2,ucd的周期T至少为多少?
[答案] (1)g 方向竖直向上 (2)见解析
[解析] (1)当A、B间加电压U0,微粒P处于平衡状态,根据平衡条件,有q=mg①
当A、B间电压为2U0时,根据牛顿第二定律,有
q-mg=ma②
由①②得a=g,加速度的方向竖直向上
(2)依题意,为使微粒P以最大的动能从小孔O1射出,应让微粒P能从O2处无初速向上一直做匀加速运动.为此,微粒P应先自由下落一段时间,然后加上电压2U0,使微粒P接着以大小为g的加速度向下减速到O2处再向上加速到O1孔射出.设向下加速和向下减速的时间分别为t1和t2,则gt1=gt2
=gt+gt,解得:t1=t2=
故应在t=T-时刻把开关S从1扳到2.
设电压ucd的最小周期为T0,向上加速过程,有
d=g2,解得:T0=6.
16.(11分)(2010·上海华师大附中摸底测试)如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的ABCD区域内,存在两个大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为L的正方形(不计粒子所受重力).
(1)在该区域AB边的中点处由静止释放电子,求电子离开ABCD区域的位置;
(2)在电场Ⅰ区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,求所有释放点的位置;
(3)若将左侧电场Ⅱ整体水平向右移动L/4,仍使电子从ABCD区域左下角D处离开(D不随电场移动),在电场Ⅰ区域内由静止释放电子的所有位置.
[答案] (1) (2)满足y1=方程的点即为所有释放点的位置 (3)在电场Ⅰ区域内满足方程y2=的所有位置
[解析] (1)由动能定理有:eEL=mv2
由类平抛运动知识有:L=vt,y=at2=×=L
所以电子离开ABCD区域的位置坐标为
(2)设释放点位置坐标为(x1,y1),由动能定理有:eEx1=mv
由类平抛运动知识有:L=v1t1,y1=at=×=
所以满足y1=方程的点即为所有释放点的位置
(3)设电子从(x2,y2)点释放,在电场Ⅰ中被加速到v2进入电场Ⅱ后做类平抛运动;在高度为y′处离开电场Ⅱ,然后做匀速直线运动并经过D处,则有
eEx2=mv
在电场Ⅱ中下降高度Δy=y2-y′=at= ·2
vy=a·=,y′=vy·
解得:y2=,即在电场Ⅰ区域内满足方程的点即为所求位置.
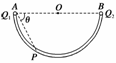
15. (10分)(2009·蚌埠一模)两个正点电荷Q1=Q和Q2=4Q分别置于固定在光滑绝缘水平面上的A、B两点正好位于水平放置的光滑绝缘半圆细管两个端点的出口处,已知AB=L,如图所示.
(1)现将另一正点电荷置于A、B连线上靠近A处静止释放,求它在AB连线上运动过程中达到最大速度时的位置离A点的距离.
(2)若把该点电荷放于绝缘管内靠近A点处由静止释放,已知它在管内运动过程中速度为最大时的位置在P处.试求出图中PA和AB连线的夹角θ.
[答案] (1) (2)arctan
[解析] (1)正点电荷在A、B连线上速度最大处对应该电荷所受合力为零(加速度最小),设此时距离A点为x,即
k=k ∴x=.
(2)点电荷在P点处若其所受库仑力的合力沿OP方向,则它在P点处速度最大,即此时满足
tanθ===,即得:θ=arctan.
14.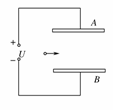 (10分)如图所示,相距为0.2m的平行金属板A、B上加电压U=40V, 在两板正中沿水平方向射入一带负电荷小球,经0.2s小球到达B板,若要小球始终沿水平方向运动而不发生偏转,A、B两板间的距离应调节为多少?(g取10m/s2)
(10分)如图所示,相距为0.2m的平行金属板A、B上加电压U=40V, 在两板正中沿水平方向射入一带负电荷小球,经0.2s小球到达B板,若要小球始终沿水平方向运动而不发生偏转,A、B两板间的距离应调节为多少?(g取10m/s2)
[答案] 0.1m
[解析] 小球在电场中做匀变速曲线运动,在竖直方向由牛顿第二定律得
mg-Uq/d=ma d/2=at2/2
解得:a=5m/s2,m=40q
要使小球沿水平方向运动,应有
 mg=E′q E′=U/d′ d′=qU/mg=0.1m
mg=E′q E′=U/d′ d′=qU/mg=0.1m
13.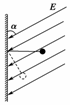 (6分)如图所示,匀强电场场强为E,与竖直方向成α角,一质量为m、电荷量为q的带负电小球用细线系在竖直墙上,恰好静止在水平位置,则场强E的大小为________.若保持场强方向和小球电荷量不变,将线拉至与场强垂直时,小球能静止,此时场强大小为________.
(6分)如图所示,匀强电场场强为E,与竖直方向成α角,一质量为m、电荷量为q的带负电小球用细线系在竖直墙上,恰好静止在水平位置,则场强E的大小为________.若保持场强方向和小球电荷量不变,将线拉至与场强垂直时,小球能静止,此时场强大小为________.
[答案]
[解析] 对两种情况下小球的受力分析如图中(a)、(b)所示,对(a)有:
Eqcosα=mg,
所以E=
对(b)有:Eq=mgcosα,
所以E=.
12.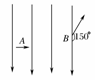 (6分)一电子以4×106m/s的速度沿与电场垂直的方向从A点水平垂直于场强方向飞入,并从B点沿与场强方向成150°的方向飞出该电场,如图所示,则A、B两点的电势差为________V.(电子的质量为9.1×10-31kg,电荷量为-1.6×10-19C)
(6分)一电子以4×106m/s的速度沿与电场垂直的方向从A点水平垂直于场强方向飞入,并从B点沿与场强方向成150°的方向飞出该电场,如图所示,则A、B两点的电势差为________V.(电子的质量为9.1×10-31kg,电荷量为-1.6×10-19C)
[答案] -136.5
[解析] 设电子射入电场时的速度为vA,射出电场时的速度为vB,从图可知vB==2vA,根据动能定理,有
W=eUAB①
W=mv-mv②
由式①②得eUAB=mv-mv=mv
所以UAB==V
=-136.5V
11. (6分)如图所示是一个平行板电容器,其电容为C,带电荷量为Q,上极板带正电,两极板间距为d.现将一个检验电荷+q由两极板间的A点移动到B点,A、B两点间的距离为s,连线AB与平行极板方向的夹角为30°,则电场力对检验电荷+q所做的功等于________.
(6分)如图所示是一个平行板电容器,其电容为C,带电荷量为Q,上极板带正电,两极板间距为d.现将一个检验电荷+q由两极板间的A点移动到B点,A、B两点间的距离为s,连线AB与平行极板方向的夹角为30°,则电场力对检验电荷+q所做的功等于________.
[答案]
[解析] 电容器两板间电势差U=,场强E==.
而A、B两点间电势差UAB=E·s·sin30°=,
电场力对+q所做功为W=qUAB=.
10.如图所示,质子、氘核和α粒子都沿平行板电容器两板中线OO′方向垂直于电场线射入板间的匀强电场,且都能射出电场,射出后都打在同一个荧光屏上,使荧光屏上出现亮点.若微粒打到荧光屏的先后不能分辨,则下列说法中正确的是 ( )
A.若它们射入电场时的速度相等,在荧光屏上将出现3个亮点
B.若它们射入电场时的质量与速度乘积相等,在荧
光屏上将出现2个亮点
C.若它们射入电场时的动能相等,在荧光屏上将只出现1个亮点
D.若它们是由同一个电场从静止加速后射入偏转电场的,在荧光屏上将只出现1个亮点
[答案] D
[解析] 粒子打在荧光屏上的位置取决于它的侧移量,侧移量相同,打在荧光屏上的位置相同,而侧移量y=,所以粒子速度相同时,屏上将出现2个亮点,粒子质量与速度乘积相同时,屏上将出现3个亮点;动能相同时,屏上将出现2个亮点;而经过同一电场从静止加速后,再进入偏转电场,出电场时所有粒子侧移量相同,屏上将出现1个亮点,故选D.
第Ⅱ卷(非选择题 共60分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com