

题目列表(包括答案和解析)
2、 用图象法求合力与分力

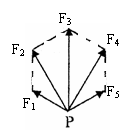 [例4]设有五个力同时作用在质点P,它们的大小和方向相当于正六边形的两条边和三条对角线,如图所示,这五个力中的最小力的大小为F,则这五个力的合力等于( )
[例4]设有五个力同时作用在质点P,它们的大小和方向相当于正六边形的两条边和三条对角线,如图所示,这五个力中的最小力的大小为F,则这五个力的合力等于( )
A、3F B、4F C、5F D、6F
解析:由正六边形的特点可知,当最小的力为F时,最大的力为2F,不难推出F1与F4合力大小为F3,即2F,方向也与F3相同,F2与F5的合力大小为F3,即2F,方向也与F3相同,故最后合力为6F。用力的三角形法则也可得出同样的结论。
物体受到多个力作用时求其合力,可将各个力沿两个相互垂直的方向直行正交分解,然后再分别沿这两个方向求出合力,正交分解法是处理多个力作用用问题的基本方法,步骤为:
①正确选择直角坐标系,一般选共点力的作用点为原点,水平方向或物体运动的加速度方向为X轴,使尽量多的力在坐标轴上。
②正交分解各力,即分别将各力投影在坐标轴上,分别求出坐标轴上各力投影的合力。
Fx=F1x+F2x+…+Fnx Fy=F1y+F2y+…+Fny
③共点力合力的大小为F= ,合力方向与X轴夹角
,合力方向与X轴夹角
规律方法
1、基本规律与方法的应用
[例1]两个力的合力与这两个力的关系,下列说法中正确的是:( CD )
A、 合力比这两个力都大
B、 合力至少比两个力中较小的力大
C、 合力可能比这两个力都小
D、 合力可能比这两个力都大
解析:(1)公式法:由合力公式F=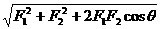 得
得
①
当θ=00时,F=F1+F2;②当θ=1800时,F=|F1-F2|;③当θ=900时,F= ;④当θ=1200且F1=F2时,F=F1=F2
;④当θ=1200且F1=F2时,F=F1=F2
可见合力可能比任何一个分力都大,也可能比任何一个分力都小,也可能等于每一个分力
(2)图象法:由三角形定则知,合力与分力的关系实际上是三角形的一个边与其它两个边的关系。由两边之和大于第三边,两边之差小于第三边,同时考虑到两个分力同向或反向的情况,合力的取值范围为| F1-F2|≤F≤(F1+F2),故答案为CD
 [例2]施用一动滑轮将一物体提起来,不计滑轮与绳的质量及其间的摩擦力,则(BCD)
[例2]施用一动滑轮将一物体提起来,不计滑轮与绳的质量及其间的摩擦力,则(BCD)
A.总可以省力一半; B.最大省力一半;
C.拉力可能大于被提物体的重量; D.拉力可能等于被提物体的重量;
解析:如图1-21所示,当拉力沿竖直方向时.省力一半,当沿2的方向上提时拉力肯定大于物体重力一半.所以A错B对,当两绳间夹角等于1200时拉力等于物体重量,所以D对,当夹角大于1200时,拉力大于物体重量,所以c对.
 说明:力是矢量,它的加减不是简单的代数加减;不共线的两个共点力与它们的合力构成三角形,利用正、余弦定理,三角形几何知识来分析相关问题,直观简捷!
说明:力是矢量,它的加减不是简单的代数加减;不共线的两个共点力与它们的合力构成三角形,利用正、余弦定理,三角形几何知识来分析相关问题,直观简捷!
[例3] A的质量是m,A、B始终相对静止,共同沿水平面向右运动。当a1=0时和a2=0.75g时,B对A的作用力FB各多大?
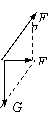 解:一定要审清题:B对A的作用力FB是B对A的支持力和摩擦力的合力。而A所受重力G=mg和FB的合力是F=ma。
解:一定要审清题:B对A的作用力FB是B对A的支持力和摩擦力的合力。而A所受重力G=mg和FB的合力是F=ma。
当a1=0时,G与 FB二力平衡,所以FB大小为mg,方向竖直向上。
当a2=0.75g时,用平行四边形定则作图:先画出重力(包括大小和方向),再画出A所受合力F的大小和方向,再根据平行四边形定则画出FB。由已知可得FB的大小FB=1.25mg,方向与竖直方向成37o角斜向右上方。
2、 按问题的需要进行分解
具体问题的条件有:
①已确定两个分力的大小,可求得分力的方向。
②已确定两个分力的方向,可求得分力的大小。
③已确定一个分力的大小和方向,可求得另上个分力的大小和方向。
④已确定一个分力的大小和另一个分力的方向,可求得一个分力的大小和另一个分力的方向。
力的分解是力的合成的逆运算,同样遵守平行四边形法则,两个分力的合力是唯一确定的,而一个已知力可以分解为大小、方向不同的分力,即一个力的两个分力不是唯一的,要确定一个力的两个分力,应根据具体条件进行。
1、 按力产生的效果进行分解
2、运算法则:
(1)平行四边形法则:求两个互成角度的共点力F1,F2的合力,可以把F1,F2的线段作为邻边作平行四边形,它的对角线即表示合力的大小和方向;
(2)三角形法则:求两个互成角度的共点力F1,F2的合力,可以把F1,F2首尾相接地画出来,把F1,F2的另外两端连接起来,则此连线就表示合力F的大小和方向;
(3)共点的两个力F1,F2的合力F的大小,与它们的夹角θ有关,θ越大,合力越小;θ越小,合力越大,合力可能比分力大,也可能比分力小,F1与F2同向时合力最大,F1与F2反向时合力最小,合力大小的取值范围是 | F1-F2|≤F≤(F1+F2)
(4)三个力或三个以上的力的合力范围在一定的条件下可以是:0≤F≤| F1+F2+…Fn|
1、求几个力的合力叫力的合成,求一个力的分力叫力的分解.
2、合力与它的分力是力的效果上的一种等效替代关系。
1、一个力如果它产生的效果跟几个力共同作用所产生的效果相同,这个力就叫做那几个力的合力,那几个力就叫做这个力的分力.
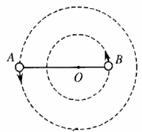
12.神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律。天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成。两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示。引力常量为G,由观测能够得到可见星A的速率 和运行周期T。
和运行周期T。
(1)可见星A所受暗星B的引力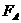 可等效为位于O点处质量为
可等效为位于O点处质量为 的星体(视为质点)对它的引力,设A和B的质量分别为
的星体(视为质点)对它的引力,设A和B的质量分别为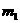 、
、 ,试求
,试求 (用
(用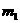 、
、 表示);
表示);
(2)求暗星B的质量 与可见星A的速率
与可见星A的速率 、运行周期T和质量
、运行周期T和质量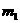 之间的关系式;
之间的关系式;
(3)恒星演化到末期,如果其质量大于太阳质量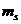 的2倍,它将有可能成为黑洞。若可见星A的速率
的2倍,它将有可能成为黑洞。若可见星A的速率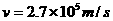 ,运行周期
,运行周期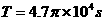 ,质量
,质量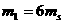 ,试通过估算来判断暗星B有可能是黑洞吗?
,试通过估算来判断暗星B有可能是黑洞吗?
( )
)
(1)设A、B的圆轨道半径分别为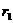 、
、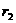 ,由题意知,A、B做匀速圆周运动的角速度相同,设其为
,由题意知,A、B做匀速圆周运动的角速度相同,设其为 。由牛顿运动定律,有
。由牛顿运动定律,有



设A、B之间的距离为 ,又
,又 ,由上述各式得
,由上述各式得
 ①
①
由万有引力定律,有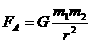 ,将①代入得
,将①代入得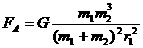
令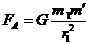 比较可得
比较可得 ②
②
(2)由牛顿第二定律,有 ③
③
又可见星A的轨道半径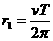 ④
④
由②③④式解得 ⑤
⑤
(3)将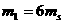 代入⑤式,得
代入⑤式,得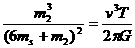
代入数据得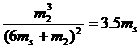 ⑥
⑥
设 ,将其代入⑥式,得
,将其代入⑥式,得 ⑦
⑦
可见,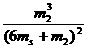 的值随
的值随 的增大而增大,试令
的增大而增大,试令
 ,得
,得
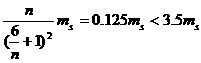 ⑧
⑧
若使⑦式成立,则 必大于2,即暗星B的质量
必大于2,即暗星B的质量 必大于2
必大于2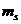 ,由此得出结论:暗星B有可能是黑洞。
,由此得出结论:暗星B有可能是黑洞。
11.宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处。(取地球表面重力加速度g=10 m/s2,空气阻力不计)
⑴求该星球表面附近的重力加速度g/;
⑵已知该星球的半径与地球半径之比为R星:R地=1:4,求该星球的质量与地球质量之比M星:M地。
解:⑴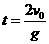
故:
⑵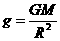 ,所以
,所以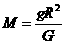
可解得:M星:M地=1´12:5´42=1:80,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com