7．一观察者站在第一节车厢前端，当列车从静止开始做匀加速运动时

A．每节车厢末端经过观察者的速度之比是1∶∶∶…∶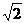

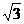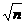
B．每节车厢末端经过观察者的时间之比是1∶3∶5∶…∶n

C．在相等时间里经过观察者的车厢数之比是1∶3∶5∶…

D．在相等时间里经过观察者的车厢数之比是1∶2∶3∶…

6．做匀加速直线运动的物体，先后经过A、B两点时的速度分别为v和7v，经

历的时间为t，则

A．前半程速度增加3.5 v

B．前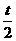时间内通过的位移为11 v t/4

C．后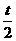时间内通过的位移为11v t/4

D．后半程速度增加3v

5．物体从斜面顶端由静止开始滑下，经t s到达中点，则物体从斜面顶端到底端

共用时间为

A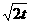．s　　　　　　　　　　　　　 B.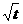s　　　　　　　　　　　　 C.2t s 　　　　　　　　　　　　　　　　 D.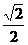t s

4．物体做匀变速直线运动，某时刻速度的大小为4 m/s，1 s后速度的大小变为10 m/s，关于该物体在这1 s内的位移和加速度大小有下列说法

①位移的大小可能小于4 m

②位移的大小可能大于10 m

③加速度的大小可能小于4 m/s²

④加速度的大小可能大于10 m/s²

其中正确的说法是

A．②④　　　　　　　　　　　 B.①④　　　　　　　　　　　　 C.②③　　　　　　　　　　　　　　　　 D.①③

3．有一个物体开始时静止在O点，先使它向东做匀加速直线运动，经过5 s，使它的加速度方向立即改为向西，加速度的大小不改变，再经过5 s，又使它的加速度方向改为向东，但加速度大小不改变，如此重复共历时20 s，则这段时间内

A．物体运动方向时而向东时而向西

B．物体最后静止在O点

C．物体运动时快时慢，一直向东运动

D．物体速度一直在增大

2．汽车以20 m/s的速度做匀速直线运动，刹车后的加速度为5 m/s2，那么开始刹车后2 s与开始刹车后6 s汽车通过的位移之比为

A．1∶4　　　　　　　　　　　 B.3∶5　　　　　　　　　 C.3∶4　　　　　　　　　　　　 D.5∶9

1．骑自行车的人沿着直线从静止开始运动，运动后，在第1 s、2 s、3 s、4 s内，通过的路程分别为1 m、2 m、3 m、4 m，有关其运动的描述正确的是

A．4 s内的平均速度是2.5 m/s

B．在第3、4 s内平均速度是3.5 m/s

C．第3 s末的即时速度一定是3 m/s

D．该运动一定是匀加速直线运动

4、圆周运动中实例分析

[例8]如图所示，是双人花样滑冰运动中男运动员拉着女运动员做圆锥摆运动的精彩场面．若女运动员做圆锥摆运动时和竖直方向的夹角为B,女运动员的质量为m,转动过程中女运动员的重心做匀速圆周运动的半径为r,求这时男运动员对女运动员的拉力大小及两人转动的角速度

解析:依圆锥摆原理,男运动员对女运动员的拉力F=mg/cosθ,女运动员做圆周运动的向心力F_向=mgtanθ,则由动力学方程得mgtanθ=mω²r,得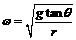

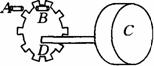[例9]如图所示为一实验小车中利用光脉冲测量车速和行程的装置的示意图,A为光源,B为电接收器,A、B均固定在车身上，C为小车的车轮，D为与C同轴相连的齿轮．车轮转动时,A发出的光束通过旋转齿轮上齿的间隙后变成脉冲光信号，被B接收并转换成电信号，由电子电路记录和显示．若实验显示单位时间内的脉冲数为n，累计脉冲数为N, 则要测出小车的速度和行程还必须测量的物理量或数据是　 　　　　　　　　；车速度的表达式为v=　　　　　 ；行程的表达式为s=　　　　　

解析：由题可知，每经过一个间隙，转化成一个脉冲信号被接收到，每个间隙转动的时间t=1/n。

设一周有P个齿轮，则有P个间隙，周期T=Pt=P/n。据v=2πR/T=2πnR/P，

所以必须测量车轮的半径R和齿数P，当肪冲总数为N，则经过的时间t₀=Nt=N/n.

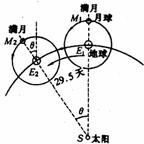所以位移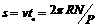

[例10]若近似认为月球绕地公转与地球绕日公转的轨道在同一平面内，且均为正圆，又知这两种转动同向，如图所示，月相变化的周期为29．5 天(图示是相继两次满月时，月、地、日相对位置的示意图)。求：月球绕地球转一周所用的时间T(因月球总是一面朝向地球，故T恰是月球自转周期)。(提示：可借鉴恒星日、太阳日的解释方法)。

3、圆周运动与其它运动的结合

圆周运动和其他运动相结合，要注意寻找这两种运动的结合点：如位移关系、速度关系、时间关系等．还要注意圆周运动的特点：如具有一定的周期性等．

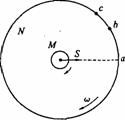[例5]如图所示，M,N是两个共轴圆筒的横截面，外筒半径为R，内筒半径比R小很多，可以忽略不计。简的两端是封闭的，两筒之间抽成真空，两筒以相同角速度。转其中心轴线(图中垂直于纸面)作匀速转动，设从M筒内部可以通过窄缝S(与M筒的轴线平行)不断地向外射出两种不同速率v₁和v₂的微粒，从S处射出时初速度方向都是沿筒的半径方向，微粒到达N筒后就附着在N筒上，如果R、v₁和v₂都不变，而ω取某一合适的值，则()

A.有可能使微粒落在N筒上的位置都在c处一条与S缝平行的窄条上

B.有可能使微粒落在N筒上的位置都在某一处如b处一条与S缝平行的窄条上

C.有可能使微粒落在N筒上的位置分别在某两处如b处和C处与S缝平行的窄条上

D.只要时间足够长，N筒上将到处落有微粒

解：微粒从M到N运动时间t=R/v,对应N筒转过角度θ=ωt=ωR/v, 即θ₁=ωt=ωR/v₁, θ₂=ωt=ωR/v₂, 只要θ₁、θ₂不是相差2π的整数倍，则落在两处，C项正确；若相差2π的整数倍，则落在一处，可能是a处，也可能是b处。A,B正确。故正确选项为ABC.

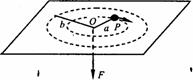
[例6]如图所示，穿过光滑水平平面中央小孔O的细线与平面上质量为m的小球P相连，手拉细线的另一端，让小球在水平面内以角速度ω₁沿半径为a的圆周做匀速圆周运动。所有摩擦均不考虑。 求：

(1)这时细线上的张力多大？

　(2)若突然松开手中的细线，经时间Δt再握紧细线，随后小球沿半径为b的圆周做匀速圆周运动。试问：Δt等于多大？这时的角速度ω₂为多大？

分析：手松后，小球不受力，将做匀速直线运动，求时间必须明确位移。正确画出松手后到再拉紧期间小球的运动情况是解题的关键。求Wz要考虑到速度的分解：小球匀速直线运动速度要在瞬间变到沿圆周切向，实际的运动可看做沿绳的切向和垂直切向的两个运动同时进行，画出速度分解图，可求得半径为b的圆周运动的速度，进而求出ω₂。

解：(1)绳的张力提供向心力：T=mω₁²a

(2)松手后小球由半径为a圆周运动到半径为b的圆周上，做的是匀速直线运动(如图所示)。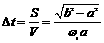

　　 小球匀速直线运动速度要在瞬间变到沿圆周切向，实际的运动可看做沿绳的切向和垂直切向的两个运动同时进行，有v₂＝vsinθ＝va/b，即　

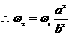
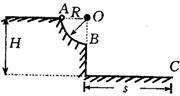
[例7]如图所示，位于竖直平面上的1／4圆轨道，半径为R，OB沿竖直方向，上端A距地面高度为H，质量为m的小球从A点由静止释放，最后落在地面上C点处，不计空气阻力，求：

(1)小球则运动到B点时，对轨道的压力多大？

(2)小球落地点C与B点水平距离S为多少？

(3)比值R／H为多少时，小球落地点C与B点水平距离S最远？该水平距离最大值是多少？

　解析：(1)小球沿圆弧做圆周运动，在B点由牛顿第二定律有N_B－mg=mv²/R　 ①

　　　 由A至B，机械能守恒，故有mgR=½mv² ②

　　　 由此解出N_B=3mg

(2)小球离B点后做平抛运动： 在竖立方向有：H－R=½gt² ③　　　 水平方向有：S＝vt　　　　 ④

　　 由②③④解出：s=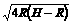　　　　 ⑤

(3)由⑤式得s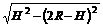＝　　　　　　 ⑥

　　 由⑥式可知当R=H/2时，s有最大值，且为s_max=H

　　 答案：N_B=3mg，s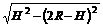＝，s_max=H

点评：对于比较复杂的问题，一定要注意分清物理过程，而分析物理过程的前提是通过分析物体的受力情况进行．

2．向心力的认识和来源

(1)向心力不是和重力、弹力、摩擦力相并列的一种类型的力，是根据力的效果命名的．在分析做圆周运动的质点受力情况时，切不可在物体的相互作用力(重力、弹力、摩擦力、万有引力)以外再添加一个向心力．

(2)由于匀速圆周运动仅是速度方向变化而速度大小不变的运动，故只存在向心加速

度，物体受的外力的合力就是向心力。显然物体做匀速圆周运动的条件是：物体的合外力大小不变，方向始终与速度方向垂直且指向圆心。

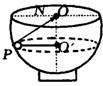(3)分析向心力来源的步骤是:首先确定研究对象运动的轨道平面和圆心的位置，然后分析圆周运动物体所受的力,作出受力图,最后找出这些力指向圆心方向的合外力就是向心力．例如，沿半球形碗的光滑内表面，一小球在水平面上做匀速圆周运动，如图小球做圆周运动的圆心在与小球同一水平面上的O^/点，不在球心O，也不在弹力N所指的PO线上．这种分析方法和结论同样适用于圆锥摆、火车转弯、飞机在水平面内做匀速圆周飞行等在水平面内的匀速圆周运动的问题。共同点是由重力和弹力的合力提供向心力，向心力方向水平。

(4)变速圆周运动向心力的分析向心力来源的步骤同分析匀速圆周运动向心力来源的步骤相向．但要注意，

①一般情况下，变速圆周运动的向心力是合外为沿半径方向的分力提供．

②分析竖直面上变速圆周运动的向心力的来源时，通常有细绳和杆两种模型．

(5)当物体所受的合外力小于所需要提供的向心力时，即F_向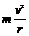＜时，物体做离心运动；当物体所受的合外力大于所需要的向心力，即F_向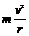＞时，物体做向心运动。

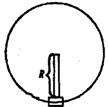[例4]飞行员从俯冲状态往上拉时，会发生黑机，第一次是因为血压降低，导致视网膜缺血，第二次是因为大脑缺血，问(1)血压为什么会降低？(2)血液在人体循环中。作用是什么？(3)为了使飞行这种情况，要在如图的仪器飞行员进行训练，飞行员坐在一个垂直平面做匀速圆周运动的舱内，要使飞行员受的加速度 a= 6g，则转速需为多少？(R＝20m)。

[解析]：(1)当飞行员往上加速上升，血液处于超重状态，视重增大，心脏无法像平常一样运输血液，导致血压降低。

(2)血液在循环中所起作用为提供氧气、营养，带走代谢所产生的废物。

(3)由a_向=v²/R可得　 v=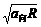＝=34．29(m/s)