
题目列表(包括答案和解析)
2、物体动量的增量可以是物体质量不变,由速度变化形成:ΔP=mv2I一mv1=m(V2一v1)=mΔv,
动量定理表达为FΔt=mΔv.也可以是速度不变,由质量变化形成:ΔP=m2v一mlv=(m2一ml)v=Δmv,动量定理表达为FΔt=ΔmV。在分析问题时要注意第二种情况。
[例4]宇宙飞船进入一个宇宙尘埃区,每前进lm,就有10个平均质量为2×10-7的微尘粒与飞船相撞,并附在飞船上。若尘埃微粒原来的速度不计,要保持飞船的速度10 km/s,飞船喷气产生的推力至少应维持多大?
解析:设飞船速度为v,飞行时间为Δt,每前进1m附着的尘粒数为n,尘粒的平均质量为m0,则在Δt内飞船增加的质量Δm=nm0vΔt.
据动量定理FΔt=Δmv。可知推力: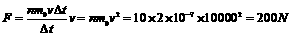
[例5]科学家设想在未来的航天事业中用太阳帆来加速星际宇宙飞船,按照近代光的粒子说,光由光子组成,飞船在太空中张开太阳帆,使太阳光垂直射到太阳帆上,太阳帆面积为S,太阳帆对光的反射率为100%,设太阳帆上每单位面积每秒到达n个光子,每个光子的动量为p,如飞船总质量为m。
求:(1)飞船加速度的表达式。
(2)若太阳帆面对阳光一面是黑色的,情况又如何?
解析:(1)设经过时间t,则在时间t内射到太阳帆上的光子数为:N=nst……①
对光子由动量定理得Ft=NP一N(一P)……② 对飞船由牛顿运动定律得F=ma……③
由以上三式解得飞船的加速度为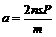
(2)若太阳帆面对阳光的一面是黑色的,则对光子由动量定理得:ft=0一N(一P)……④
由①③④得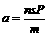
[例6]自动称米机已在许多大粮店广泛使用。买者认为:因为米流落到容器中时有向下 的冲力而不划算;卖者则认为:当预定米的质量数满足时,自动装置即刻切断米流时,此刻尚有一些米仍在空中,这些米是多给买者的,因而双方争执起来,究竟哪方说得对而划算呢?(原理如图所示)。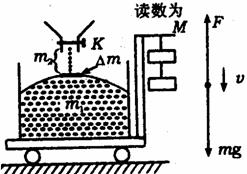
解析:设米流的流量为dkg/s,它是恒定的,自动装置能即刻在出口处切断米流,米流在出口处速度很小可视为零,若切断米流后,盛米的容器中静止的那部分米的质量为m1kg,空中还在下落的米质量为m2kg,则落到已静止的米堆(m1)上的一小部分米的质量为Δm kg.取Δm为研究对象,这部分米很少,在Δt时间内Δm=d·Δt,设其落到米堆上之前的速度为V,经Δt时间静止,其受力如图所示,由动量定律得
(F一Δmg)Δt=ΔmV 即F=dV十d·Δt·g
根据牛顿第三定律知F=F/, 称米机的读数应为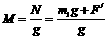 =m1+m2+Δm
=m1+m2+Δm
可见,称米机读数包含了静止在袋中的部分m1,也包含了尚在空中的下落的米流 m2应包含刚落至米堆上的一小部分Δm,即自动称米机是准确的,不存在哪方划算不划算的问题。
点评:本例是物理知识在实际生活中应用综合题,涉及物理中的冲量,动量、动量守恒、牛顿第三定律等知识。考查学生应用学科知识解决实际问题的能力,解此题必须正确分析现象,形成正确的物理图景,恰当运用物理规律求解。
1、动量定理FΔt=mvt-mv0可以用一种更简洁的方式FΔt=ΔP表达,式中左边表示物体受到的冲量,右边表示动量的增量(变化量)。此式稍加变形就得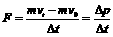
其含义是:物体所受外力(若物体同时受几个力作用,则为合外力)等于物体动量的变化率。这一公式通常称为“牛顿第二定律的动量形式”。这一形式更接近于牛顿自己对牛顿第二定律的表述。应用这个表述我们在分析解决某些问题时会使思路更加清晰、简洁。
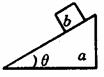 [例1]如图所示,在粗糙水平面上放一三角本块a,若物体b在a的斜面上静止,加速,匀速或减速下滑时.在四种情况下a对平面的压力比a、b两重力之和大还是小?
[例1]如图所示,在粗糙水平面上放一三角本块a,若物体b在a的斜面上静止,加速,匀速或减速下滑时.在四种情况下a对平面的压力比a、b两重力之和大还是小?
解法一:(常规解法)如图所示,
N=Ga+Ny+fy
 Ny=Nb-acosθ=Gbcos2θ
Ny=Nb-acosθ=Gbcos2θ
fy=fb-asinθ,当b沿斜面匀速下滑时,在数值上fb-a=fa-b= Gbsinθ
所以fy=Gbsin2θ
所以 N= Ga+Gbsin2θ+Gbcos2θ=Ga+Gb
当b在a上静止时情形亦如此N=Ga+Gb
当b在a上加速下滑时f<Gbsinθ,所以 N<Ga+Gb
当b在a上减速下滑时f>Gbsinθ,所以N>Ga+Gb
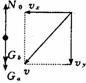 解法二:将a、b视为一整体如图所示,将N分解
解法二:将a、b视为一整体如图所示,将N分解
根据动量定理[N0-(Ga+Gb )]Δt=ΔP
显然匀速运动时N= Ga+Gb
加速运动时N<Ga+Gb
减速运动时N>Ga+Gb
下面我们再来讨论a与地面间摩擦力的方向
(1)当b沿料面匀速运动或静止在斜面上;
(2)当b沿斜面加速下滑;
(3)当b沿斜面减速下滑;
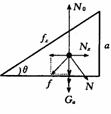 (4)当b沿斜面向上运动.
(4)当b沿斜面向上运动.
解法一:(l)当b静止在斜面或沿料面匀速下滑时对b有:Gbsinθ=f N=Gbcosθ
对a受力分析如图所示,比较fx与Nx的大小
fx=fcosθ= Gbsinθcosθ,Nx=Gbcosθsinθ
所以当b静止或沿料面匀速下滑时,fx=Nx,a与平面间无摩擦力.
(2)当b沿斜面加速下滑时对b ,Gbsinθ>f所以对a ,fx<Nx,摩擦力方向向左
(3)当b沿斜面减速下滑时 Gbsinθ<f所以对a,fx>Nx,摩擦力方向向右
(4)当b沿斜面向上运动时,a受到b对它摩擦力的方向斜向上,很显然地面对a摩擦力方向向左.
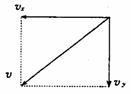 解法二:将ab视为一个系统,将b的速度分解如图所示,
解法二:将ab视为一个系统,将b的速度分解如图所示,
(1)当停止或匀速下滑时,Δvx=0.
根据动量定理,ab在水平方向受到冲量为零,所以产生冲量的摩擦力为零.
(2)当沿斜面加速下滑时fΔt=mbΔvx,f与Δvx同向,所以f方向向左.
(3)当沿斜面减速下滑时:我们可用同样方法得出f方向向右.
注意:当b沿斜面向上匀速运动时,Δvx=0,由动量定理可知,f应当为零,而实际上方向向左,为什么?这里必须清楚.当b沿斜面向上匀速运动时,对这个系统,水平方向的合外力已经不单是f了,必须有除f以外的外力存在,而且它的方向或者其分力方向水平向右,否则b不会沿斜面向上匀速运动.
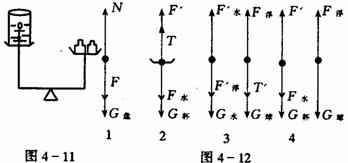
[例2]如图所示,等臂天平左端有一容器,内盛有水,水中有一密度小于水密度的木球.有一细绳一端系球,一端固定于烧杯底部,整个系统处于平衡状态,假设细绳突然断裂,小球相对于水向上加速运动,天平将如何?
 解法一:按照常规则应进行如下分析
解法一:按照常规则应进行如下分析
对盘:如图4-12中1所示(N为臂对盘的支持力,F为杯对盘的压力)
N=F+G盘 ①
对杯底:如图4-12中2所示(F/为盘对杯的支持力,T为绳对杯的拉力,F水为水对杯的压力)
F/=F F/=G杯+F水-T ②
对水:如图4-12中3所示( F/水为杯底对水的支持力,F/浮为球对水作用力)
F/水= F/浮十G水 ③
对球(F浮为水对球的浮力,T/为绳对球的拉力,T/= T)F浮=F/浮
当静止时 F浮=T/十 G球 代入③得 F/水=T/十G球 + G水 代入②得
F/= G杯十 G水+G球 代入①得 N=G盘+G杯十 G水+G球
当绳断时,对杯底如图4-12中4所示,
F/=G杯+ G水 ④
F浮一G球=m木球a-m水球a 即F浮 =G球十m木球a-m水球a 代入③得
对水F/水= G球+G水+m木球a-m水球a 代入④得
F=G杯十G水十G球十m木球a-m水球a 代入①得 N=G盘+G杯十 G水+G球十m木球a-m水球a 所以天平左端上升.
解法二:若将盘、杯、水、球视为一个整体,则根据动量定理 FΔt=ΔP
即[N(G盘+G杯十 G水+G球 )]Δt=ΔP
当静止时ΔP=0 所以 N=G盘+G杯十 G水+G球
当木球向上运动水球向下运动时,ΔP=m木球Δv-m水球Δv<0 所以 N<G盘+G杯十 G水+G球 从而知天平左端上升.
说明:前法较后法步骤繁杂,使人接受困难,后法两步即可得出结论,两法比较,繁简分明.
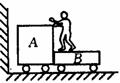 [例3]如图所示,在光滑水平面上,有A、B两辆小车.水平面左侧有一竖直墙.在小车B上坐着一个小孩.小孩与车B的总质量是车A的10倍,两车从静止开始,小孩把车A以对地速度v推出,车A与墙碰撞后仍以原速率返回,小孩接到车A后,又把它以对地速度v推出,车A返回后,小孩再把它推出,每次推出,小车A对地速度都是v,方向向左,则小孩共把车A推出多少次后,车A返回小孩不能再接到?
[例3]如图所示,在光滑水平面上,有A、B两辆小车.水平面左侧有一竖直墙.在小车B上坐着一个小孩.小孩与车B的总质量是车A的10倍,两车从静止开始,小孩把车A以对地速度v推出,车A与墙碰撞后仍以原速率返回,小孩接到车A后,又把它以对地速度v推出,车A返回后,小孩再把它推出,每次推出,小车A对地速度都是v,方向向左,则小孩共把车A推出多少次后,车A返回小孩不能再接到?
解析:题中车A多次与车B及墙壁间发生相互作用,而每次与车B作用时,水平方向合力为0,故A、B每次作用时,由车A与车B组成系统动量守恒,而每次作用后车B的速度是下一次作用前的速度,这为一个隐含条件,车A返回,小孩不能接到的临界条件是vB=v.
设第一次、第二次、…、第n次作用后,车B的速度为v1,v2,…,vn,每次作用,车A与车B动量守恒,从而得到
0=10mvl-mv ………① (A、B第1次作用)
10mvl +mv=10mv2-mv ………② (A、B第2次作用)
10mv2 +mv=10mv3-mv ………③ (A、B第3次作用)
………
10mvn-1 +mv=10mvn-mv (A、B第n次作用)
把n式相加得:(n-1)mv= 10mvn-nmv
即得:vn= v≥v
则 n≥5.5, n取整数, n=6次后,车A 返回时,小孩接不到车A
v≥v
则 n≥5.5, n取整数, n=6次后,车A 返回时,小孩接不到车A
巧解:对A、B系统,所受合外力就是墙的弹力.这个弹力每次产生冲量大小为2mv,要使B不再接到 A,必须vA≤vB.这里先取一个极限值vA=vB=v ,则:
根据动量定理, n2mv=(M+m)v
将M=10m代入解得 n=5.5,所以推6次即可.
2、速度--时间图象的迁移与妙用
 [例4] 一个固定在水平面上的光滑物块,其左侧面是斜面AB,右侧面是曲面AC。已知AB和AC的长度相同。两个小球p、q同时从A点分别沿AB和AC由静止开始下滑,比较它们到达水平面所用的时间
[例4] 一个固定在水平面上的光滑物块,其左侧面是斜面AB,右侧面是曲面AC。已知AB和AC的长度相同。两个小球p、q同时从A点分别沿AB和AC由静止开始下滑,比较它们到达水平面所用的时间
A.p小球先到 B.q小球先到 C.两小球同时到 D.无法确定
解:可以利用v-t图象(这里的v是速率,曲线下的面积表示路程s)定性地进行比较。在同一个v-t图象中做出p、q的速率图线,显然开始时q的加速度较大,斜率较大;由于机械能守恒,末速率相同,即曲线末端在同一水平图线上。为使路程相同(曲线和横轴所围的面积相同),显然q用的时间较少。
 [例5] 两支完全相同的光滑直角弯管(如图所示)现有两只相同小球a和a/ 同时从管口由静止滑下,问谁先从下端的出口掉出?(假设通过拐角处时无机械能损失)
[例5] 两支完全相同的光滑直角弯管(如图所示)现有两只相同小球a和a/ 同时从管口由静止滑下,问谁先从下端的出口掉出?(假设通过拐角处时无机械能损失)
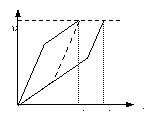 解:首先由机械能守恒可以确定拐角处v1> v2,而两小球到达出口时的速率v相等。又由题薏可知两球经历的总路程s相等。由牛顿第二定律,小球的加速度大小a=gsinα,小球a第一阶段的加速度跟小球a/第二阶段的加速度大小相同(设为a1);小球a第二阶段的加速度跟小球a/第一阶段的加速度大小相同(设为a2),根据图中管的倾斜程度,显然有a1> a2。根据这些物理量大小的分析,在同一个v-t图象中两球速度曲线下所围的面积应该相同,且末状态速度大小也相同(纵坐标相同)。开始时a球曲线的斜率大。由于两球两阶段加速度对应相等,如果同时到达(经历时间为t1)则必然有s1>s2,显然不合理。考虑到两球末速度大小相等(图中vm),球a/ 的速度图象只能如实线所示。因此有t1< t2,即a球先到。
解:首先由机械能守恒可以确定拐角处v1> v2,而两小球到达出口时的速率v相等。又由题薏可知两球经历的总路程s相等。由牛顿第二定律,小球的加速度大小a=gsinα,小球a第一阶段的加速度跟小球a/第二阶段的加速度大小相同(设为a1);小球a第二阶段的加速度跟小球a/第一阶段的加速度大小相同(设为a2),根据图中管的倾斜程度,显然有a1> a2。根据这些物理量大小的分析,在同一个v-t图象中两球速度曲线下所围的面积应该相同,且末状态速度大小也相同(纵坐标相同)。开始时a球曲线的斜率大。由于两球两阶段加速度对应相等,如果同时到达(经历时间为t1)则必然有s1>s2,显然不合理。考虑到两球末速度大小相等(图中vm),球a/ 的速度图象只能如实线所示。因此有t1< t2,即a球先到。
[例6]一只老鼠从洞口爬出后沿一直线运动,其速度大小与其离开洞口的距离成反比。当其到达距洞口为d1的A点时速度为v1.若B点离洞口的距离为d2(d2>d1),求老鼠由A运动至B所需的时间。
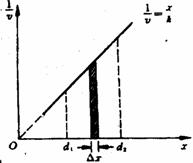 [解析]图中的曲线与横轴所围面积的数值正是老鼠经过一定的位移所需的时间。如图所示,取一窄条,其宽度Δx很小(Δx→0),此段位移所需时间Δt也很小(Δv→0),可以认为在如此短时间内,老鼠的速度改变很小(Δv→0),如图中窄条的面积为A=Δx
[解析]图中的曲线与横轴所围面积的数值正是老鼠经过一定的位移所需的时间。如图所示,取一窄条,其宽度Δx很小(Δx→0),此段位移所需时间Δt也很小(Δv→0),可以认为在如此短时间内,老鼠的速度改变很小(Δv→0),如图中窄条的面积为A=Δx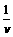 =
=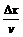 ,这正表示老鼠经位移Δx所需的时间。故图中,图线
,这正表示老鼠经位移Δx所需的时间。故图中,图线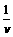 =
= ,x1=dl,x2=d2及x轴所围的梯形面积正是老鼠由dl爬至d2所需的时间。K=v1d1=v2d2;T=
,x1=dl,x2=d2及x轴所围的梯形面积正是老鼠由dl爬至d2所需的时间。K=v1d1=v2d2;T=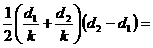
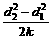
 。
。
说明:利用图象的物理意义来解决实际问题往往起到意想不到的效果.在中学阶段某些问题根本无法借助初等数学的方法来解决,但如果注意到一些图线的斜率和面积所包含的物理意义,则可利用比较直观的方法解决问题。
[例7]甲、乙两车同时同向沿直线驶向某地,甲在前一半时间以v1匀速运动,后一半时间以v2匀速运动.乙在前一半路程以v1匀速运动,后一半路程以v2匀速运动,先到目的地的是____.
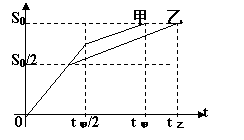
|
[例8]质点P以O点为平衡位置竖直向上作简谐运动,同时质点Q也从O点被竖直上抛,它们恰好同时到达最高点,且高度相同,在此过程中,两质点的瞬时速度vP与vQ的关系应该是 [ D ]
 A.vP>vQ. B.先vP>vQ,后vP<vQ,最后vP=vQ=0.
A.vP>vQ. B.先vP>vQ,后vP<vQ,最后vP=vQ=0.
C.vP<vQ. D.先vP<vQ,后vP>vQ,最后vP=vQ=0.
解析:这也是用解析方法很难下手的题目,但若能利用题设条件,画好、分析好两个质点的v-t图线,就能很快找到答案.
先在图中画出Q作匀减速运动的v-t图象.由于P作简谐运动,当它由平衡位置向极端位置运动过程中,受到的回复力从零开始不断变大,它的加速度也从零开始不断变大,速度不断变小,P作加速度不断增大的减速运动,其v-t图线是一条曲线.根据v-t图线上任一点的切线的斜率数值上等于质点在该时刻的加速度,由于P的加速度由零开始不断变大,画出曲线切线斜率的绝对值也应由零开始不断增大,即曲线的切线应从呈水平状态开始不断变陡,那么只有向右边凸出的下降的曲线才能满足这样的条件.又因P与Q的运动时间相等,所以曲线的终点也应在t,P与Q的路程相等,所以曲线包围的面积应等于三角形vQ0Ot的面积,根据这些要求,曲线的起点,即质点P的初速度vP0必定小于Q的初速vQ0,且两条v-t图线必定会相交,如图7中的实线所示.图7的两条虚线表示的质点P的v-t图线都不满足题设条件(P与Q的路程相等),所以(D)选项正确.
1、s--t图象和v--t图象的应用
[例1]甲、乙、两三物体同时同地开始做直线运动,其位移一时间图象如图所示,则在t0时间内,甲、乙、丙运动的平均速度的大小关系分别是:V甲 V乙 V丙(填“>”、“=”或“<”),它们在t0时间内平均速率大小关系为V/甲_V/乙_V/丙·
解析:由图可知,在t0时间内它们的位移相同,由平均速度的定义,故可知甲、乙、两三者在t0时间内的平均速度的大小相同,即V甲=V乙=V丙,而平均速率是指质点运动的路程(质点运动轨迹的长度)与时间的比值,由图中可知,质点在to时间内,甲的路程最长,(由图象中可知甲有回复运动)故甲的平均速率最大,而乙和丙路程相同,故乙和丙的平均速率相同,即V/甲>V/乙=V/丙.
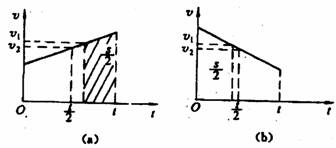 注意:平均速率不是平均速度的大小.对于图象问题,要求把运动物体的实际运动规律与图象表示的物理含义结合起来考虑.
注意:平均速率不是平均速度的大小.对于图象问题,要求把运动物体的实际运动规律与图象表示的物理含义结合起来考虑.
[例2]物体沿一直线运动,在t时间内通过的路程为S。它在中间位置½S处的速度为v1,在中间时刻½t时的速度为v2,则v1、v2的关系为
A.当物体作匀加速直线运动时,v1>v2
B.当物体作匀减速直线运动时,v1<v2;
c.当物体作匀速直线运动时,v1=v2
D.当物体作匀减速直线运动时,v1>v2
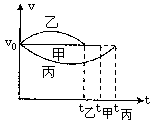 [解析]由题意,作出物体的v一t关系图,½S点处的虚线把梯形面积一分为二,如图所示,由图可知,无论物体作匀加速直线运动还是作匀减速直线运动。在路程中间位置的速度v1始终大于中间时刻的速度v2,当物体作匀速直线运动时,在任何位置和任何时刻的速度都相等。
[解析]由题意,作出物体的v一t关系图,½S点处的虚线把梯形面积一分为二,如图所示,由图可知,无论物体作匀加速直线运动还是作匀减速直线运动。在路程中间位置的速度v1始终大于中间时刻的速度v2,当物体作匀速直线运动时,在任何位置和任何时刻的速度都相等。
故正确答案A、C、D。
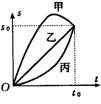
[例3]甲、乙、丙三辆汽车以相同的速度同时经过某一路标,从此时开始,甲车一直做匀速直线运动,乙车先加速后减速,丙车先减速后加速,它们经过下一路标时速度又相同,则哪一辆车先经过下一个路标?
解析:由题可知这三辆汽车的初、末速度相同,它们发生的位移相同,而题中并不知乙、丙两车在各阶段是否做匀速直线运动,因此,我们只能分析它们的一般运动,即变速直线运动,这样匀变速直线运动的规律就无法求解这一问题,如果我们利用图象法,即在同一坐标系中,分别做出这三辆车的v-t图象,如图所示,由此可知:乙车到达下一个路标的时间最短,即乙车最先通过下一个路标。
 说明:图象法是根据物体的运动规律及题中条件,将复杂的运动过程转化成简单、直观过程的一种思维方法。
说明:图象法是根据物体的运动规律及题中条件,将复杂的运动过程转化成简单、直观过程的一种思维方法。
2、速度时间图象
(1)它反映了运动物体速度随时间的变化关系.
(2)匀速运动的V一t图线平行于时间轴.
(3)匀变速直线运动的V-t图线是倾斜的直线,其斜率数值上等于物体运动的加速度.
(4)非匀变速直线运动的V一t图线是曲线,每点的切线方向的斜率表示该点的加速度大小.
 规律方法
规律方法
(1)s--t图象和v--t图象,只能描述直线运动--单向或双向直线运动的位移和速度随时间的变化关系,而不能直接用来描述方向变化的曲线运动。
(2)当为曲线运动时,应先将其分解为直线运动,然后才能用S-t或v一t图象进行描述。
1、位移时间图象
位移时间图象反映了运动物体的位移随时间变化的关系,匀速运动的S-t图象是直线,直线的斜率数值上等于运动物体的速度;变速运动的S-t图象是曲线,图线切线方向的斜率表示该点速度的大小.
a.从图象识别物体运动的性质。
b.能认识图像的截距的意义。
C.能认识图像的斜率的意义。
d.能认识图线覆盖面积的意义。
e.能说出图线上一点的状况。
3、两种运动的联系与应用
[例6]自高为H的塔顶自由落下A物的同时B物自塔底以初速度v0竖直上抛,且A、B两物体在同一直线上运动.下面说法正确的是( )
A.若v0>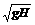 两物体相遇时,B正在上升途中 B、v0=
两物体相遇时,B正在上升途中 B、v0=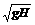 两物体在地面相遇
两物体在地面相遇
C.若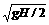 <v0<
<v0<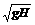 ,两物体相遇时B物正在空中下落
,两物体相遇时B物正在空中下落
D.若v0=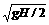 ,则两物体在地面相遇
,则两物体在地面相遇
解析:由A、B相对运动知,相遇时间t=H/ v0,B物上升到最高点需时间t1= v0/g.落回到抛出点时间t2=2v0/g
要在上升途中相遇,t<t1,即H/ v0<v0/g。v0>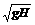 ,要在下降途中相遇.t1<
t< t2,即v0/g<H/
v0<2v0/g.
,要在下降途中相遇.t1<
t< t2,即v0/g<H/
v0<2v0/g.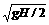 <v0<
<v0<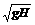
在最高点相遇时t=t1,vo=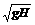 ; 在地面相遇时.t=t2,vo=
; 在地面相遇时.t=t2,vo=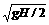 .
.
答案:ACD
[例7]子弹从枪口射出速度大小是30m/s,某人每隔1s竖直向上开一枪,假设子弹在升降过程中都不相碰,试求
(1)空中最多能有几颗子弹?
(2)设在t=0时将第一颗子弹射出,在哪些时刻它和以后射出的子弹在空中相遇而过?
(3)这些子弹在距原处多高的地方与第一颗子弹相遇?(不计空气阻力,g取10m/s2)
解:(1)设子弹射出后经ts回到原处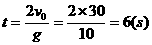
t=0时第一颗子弹射出,它于第6s末回到原处时,第七颗子弹射出,所以空中最多有六颗子弹.
(2)设第一颗子弹在空中运动t1s,和第二颗子弹在空中相遇.V1=v0-gt,V2=v0-g(t1-1)
由对称性v2=-v1,即v0-g(t1-1)=gt1-v0 解得 t1=3.5(s)
同理,第一颗子弹在空中运动t2=4.0s、t3=4.5s、t4=5.0s、t5=5.5s分别与第三颗子弹、第四颗子弹、第五颗子弹、第六颗子弹在空中相遇.
(3)由 ,将t1=3.5s,t2=4.0s,t3=4.5s,t4=5.0s和 t5=5.5s分别代入上式,得h1=43.75m,h2=40m,h3=33.75m,h4=25m,h5=13.75m。
,将t1=3.5s,t2=4.0s,t3=4.5s,t4=5.0s和 t5=5.5s分别代入上式,得h1=43.75m,h2=40m,h3=33.75m,h4=25m,h5=13.75m。
2、充分运用竖直上抛运动的对称性
(1)速度对称:上升和下降过程经过同一位置时速度等大反向。
(2)时间对称:上升和下降过程经过同一段高度的上升时间和下降时间相等。
[例4]某物体被竖直上抛,空气阻力不计,当它经过抛出点之上0.4m时,速度为3m/s.它经过抛出点之下0.4m时,速度应是多少?(g=10m/s2)
解法一:竖直上抛物体的上抛速度与落回原抛出点速度大小相等.因此,物体在抛出点之上0.4m处,上升阶段或下降阶段的速度大小都是3m/s.若以下落速度3m/s为初速度,0.4+0.4(m)为位移量,那么所求速度就是设问的要求.
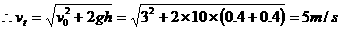
解法二 :物体高度为h1=0.4m时速度为v1,则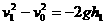
物体高度为h2=-0.4m时速度为v2,则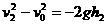
由以上两式式消去v0得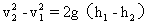 ,
,
[例5]一个从地面竖直上抛的物体,它两次经过一个较低的点a的时间间隔是Ta,两次经过一个较高点b的时间间隔是Tb,则a、b之间的距离为( )
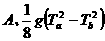 ;
; 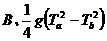 ;
;
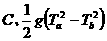 ;
; 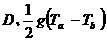
解析:根据时间的对称性,物体从a点到最高点的时间为Ta/2,从b点到最高点的时间为Tb/2,所以a点到最高点的距离ha=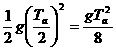 ,b点到最高点的距离hb=
,b点到最高点的距离hb=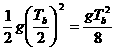 ,
,
故a、b之间的距离为ha-hb=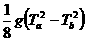 ,即选A
,即选A
1、基本规律的理解与应用
[例1]从一定高度的气球上自由落下两个物体,第一物体下落1s后,第二物体开始下落,两物体用长93.1m的绳连接在一起.问:第二个物体下落多长时间绳被拉紧.
解法一 设第二个物体下落ts后绳被拉紧,此时两物体位移差Δh=93.1m
Δh=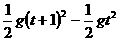 ,即93.1=
,即93.1=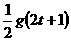 ,解得 t=9(s)
,解得 t=9(s)
解法二 以第二个物体为参照物.在第二个物体没开始下落时,第一个物体相对第二个物体做自由落体运动;1s后,第二个物体开始下落,第一个物体相对第二个物体做匀速运动,其速度为第一个物体下落1s时的速度.当绳子被拉直时,第一个物体相对第二个物体的位移为h=93.1m.h=h1+h2
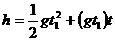 ,即
,即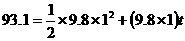 解得 t=9(s)
解得 t=9(s)
[例2]利用水滴下落可以测量重力加速度g,调节水龙头,让水一滴一滴地流出。在水龙头的正下方放一个盘子,调整盘子的高度,使一个水滴碰到盘子时,恰好有另一个水滴从水龙头开始下落,而空中还有一个正在下落的水滴。测出水龙头到盘子的距离为h,再用秒表测时间。从第一个水滴离开水龙头开时计时,到第n个水滴落到盘子中,共用时间为t0问:第一个水滴落到盘中时,第二个水滴离开水龙头的距离为多少?可测得的重力加速度为多少?
[解析]由于水龙头滴水的时间间隔是恒定的,因此,题中所提到的某一时刻恰好滴到盘子的水滴和正在空中下落的水滴,这两个水滴的状态可以看做是同一个水滴离开水龙头做自由落体运动的两个状态:滴到盘子的水滴运动时间为2t1,正在空中下落的水滴的位置相当于下落时间为t1的位置,通过比例关系可解每个水滴在下落的一半时间内的下落高度即为所求。依题意数清楚在计时t内有多少个水滴离开水龙头,就得到了相邻两滴水滴落下的时间间隔,将此时间间隔用于开始下落的过程上,可解出重力加速度的表达式。
解:滴水的时间间隔恒定,视为同一滴水在下落h段的时间分为相等的两段,前段时间内下落h1.则由初速为零的匀加速直线运动的比例关系,有:hl:h=1:4;而hl就是第一个水滴落到盘中时,第二个水滴离开水龙头的距离: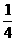 h0。从开始计时到第n个水滴落到盘子中,共有(n+1)个水滴离开水龙头,相邻两滴水滴落下的时间间隔为t1=
h0。从开始计时到第n个水滴落到盘子中,共有(n+1)个水滴离开水龙头,相邻两滴水滴落下的时间间隔为t1=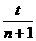 。
。
从开始下落经历t1下落了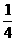 h,由
h,由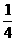 h=
h=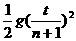 得:g=
得:g=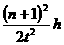
[例3]将一轻质球竖直上抛,若整个运动过程中,该球所受空气阻力大小不变,上升时间为t上,下降时间为 t下,抛出时速度为 v0,落回时速度为vt,则它们间的关系是( )
A.t上>t下,v0>vt; B.t上<t下,v0<vt C.t上<t下,v0>vt;D.t上=t下,v0=vt
解析:a上=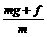 ,a下=
,a下= ,所以a上>a下. t上=
,所以a上>a下. t上=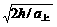 ,t下=
,t下=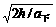 。所以t上<t下,v0=
。所以t上<t下,v0=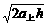 ,vt=
,vt=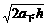 ,所以v0>vt 答案:C
,所以v0>vt 答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com