1．电功:电荷在电场中移动时,电场力做的功W＝UIt，

电流做功的过程是电能转化为其它形式的能的过程.

3、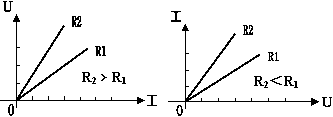导体的伏安特性曲线:研究部分电路欧姆定律时,常画成I-U或U-I图象,对于线性元件伏安特性曲线是直线,对于非线性元件,伏安特性曲线是非线性的.

注意：①我们处理问题时，一般认为电阻为定值，不可由R=U/I认为电阻R随电压大而大，随电流大而小．

②I、U、R必须是对应关系．即I是过电阻的电流，U是电阻两端的电压．

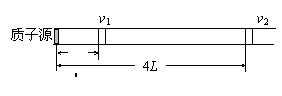
[例1]来自质子源的质子(初速度为零)，经一加速电压为800kV的直线加速器加速，形成电流强度为1mA的细柱形质子流。已知质子电荷e=1.60×10^-19C。这束质子流每秒打到靶上的质子数为_________。假定分布在质子源到靶之间的加速电场是均匀的，在质子束中与质子源相距L和4L的两处，各取一段极短的相等长度的质子流，其中的质子数分别为n₁和n₂，则n₁∶n₂=_______。

解：按定义，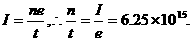

　　 由于各处电流相同，设这段长度为l，其中的质子数为n个，

则由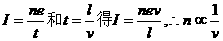。而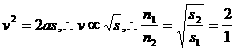

点评：解决该题的关键是：(1)正确把握电流强度的概念 I＝Q/t而 Q＝ne。所以n=Q/e=It/e,(2)质子源运动路程上的线密度与其瞬时速度成反比，因为I＝neSv，所以当电流I一定时，n与v成反比．

[例2]用某种金属制成粗细均匀的导线，通以一定大小的恒定电流，过一段时间后，导线升高的温度(　　　　　 )

A．跟导线的长度成正比　　　　　　　　 B．跟导线的长度成反比

C．跟导线的横截面积成正比　　　　　　 D．跟导线的横截面积成反比

解析：金属导线的电阻为R＝ρL／S，通电后产生的电热为Q＝I²Rt＝I²ρt／S．设金属导体升高的温度为ΔT，由热学知识可知导体需要的热量为 Q^／＝cmΔT＝ cρ_密 LSΔT．电流产生的全部热量均被导线所吸收，即：I²ρt／S＝cρ_密 LSΔT，ΔT＝I²ρt／cρ_密LS²，上式说明了 D选项正确．

2、适用于金属导电体、电解液导体，不适用于空气导体和某些半导体器件．

1、导体中的电流I跟导体两端的电压成正比，跟它的电阻R成反比。 I=U/R

3．半导体与超导体

(1)半导体的导电特性介于导体与绝缘体之间,电阻率约为10^－5Ω·m -10⁶Ω·m

(2)半导体的应用:

①热敏电阻:能够将温度的变化转成电信号,测量这种电信号,就可以知道温度的变化.

②光敏电阻:光敏电阻在需要对光照有灵敏反应的自动控制设备中起到自动开关的作用.

③晶体二极管、晶体三极管、电容等电子元件可连成集成电路.

④半导体可制成半导体激光器、半导体太阳能电池等.

(3)超导体

①超导现象：某些物质在温度降到绝对零度附近时,电阻率突然降到几乎为零的现象.

②转变温度(T_C):材料由正常状态转变为超导状态的温度

③应用:超导电磁铁、超导电机等

2．电阻、电阻定律　　　

(1)电阻:加在导体两端的电压与通过导体的电流强度的比值.

R=U/I,导体的电阻是由导体本身的性质决定的,与U.I无关.

(2)电阻定律:导体的电阻R与它的长度L成正比,与它的横截面积S成反比. R＝ρL/S

(3)电阻率:电阻率ρ是反映材料导电性能的物理量，由材料决定,但受温度的影响．

①电阻率在数值上等于这种材料制成的长为1m,横截面积为1m²的柱形导体的电阻.

②单位是:Ω·m.

1．电流：电荷的定向移动形成电流．

(1)形成电流的条件：内因是有自由移动的电荷，外因是导体两端有电势差．

(2)电流强度：通过导体横截面的电量Q与通过这些电量所用的时间t的比值。

①I=Q/t；假设导体单位体积内有n个电子，电子定向移动的速率为V，则I=neSv；假若导体单位长度有N个电子，则I＝Nev．

②表示电流的强弱，是标量．但有方向，规定正电荷定向移动的方向为电流的方向．

③单位是：安、毫安、微安1A=10³mA=10⁶μA

5.介质中质点的振动方向未定

　　 在波的传播过程中，质点振动方向与传播方向联系，若某一质点振动方向未确定，则波的传播方向有两种，这样形成多解．

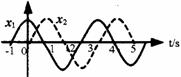　 说明：波的对称性：波源的振动要带动它左、右相邻介质点的振动，波要向左、右两方向传播．对称性是指波在介质中左、右同时传播时，关于波源对称的左、右两质点振动情况完全相同．

[例3]一列在x轴上传播的简谐波，在x_l= 10cm和x₂=110cm处的两个质点的振动图象如图所示，则质点振动的周期为

　　　　　　 s，这列简谐波的波长为　　　　 cm．

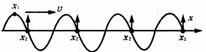　 [解析]由两质点振动图象直接读出质点振动周期为 4s．由于没有说明波的传播方向，本题就有两种可能性：(1)波沿x轴的正方向传播．在t＝0时，x₁在正最大位移处，x₂在平衡位置并向y轴的正方向运动，那么这两个质点间的相对位置就有如图所示的可能性，也就x₂一 x₁＝(n十1/4)λ，λ=400/(1十4n)cm

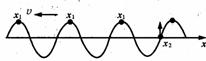(2)波沿x轴负方向传播．在t＝0时．x₁在正最大位移处，x₂在平衡位置并向y轴的正方向运动，那么这两个质点间的相对位置就有如图所示的可能性，x₂一 x₁＝(n十3/4)λ，λ=400／(3+ 4n)cm　　　　　

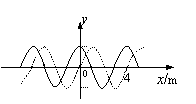点评：由于波在媒质中传播具有周期性的特点，其波形图每经过一个周期将重复出现以前的波形图，所以由媒质中的质点的振动图象确定波长的值就不是唯一的(若要是唯一的，就得有两个前提：一个是确定波传播方向；一个是确定波长的范围)．

[例4]如图实线是某时刻的波形图象，虚线是经过0.2s时的波形图象。求：

①波传播的可能距离 ②可能的周期(频率)

③可能的波速　 ④若波速是35m/s，求波的传播方向　

⑤若0.2s小于一个周期时，传播的距离、周期(频率)、波速。

解析：①题中没给出波的传播方向，所以有两种可能：向左传播或向右传播。

向左传播时，传播的距离为x=nλ+3λ/4=(4n+3)m　 (n=0、1、2　 …)

向右传播时，传播的距离为x=nλ+λ/4=(4n+1)m　 (n=0、1、2　 …)

②向左传播时，传播的时间为t=nT+3T/4得：T=4t/(4n+3)=0.8 /(4n+3)(n=0、1、2　 …)

向右传播时，传播的时间为t=nT+T/4得：T=4t/(4n+1)=0.8 /(4n+1)　 (n=0、1、2　 …)

③计算波速，有两种方法。v=x/t　 或v=λ/T

向左传播时，v=x/t=(4n+3)/0.2=(20n+15)m/s. 或v=λ/T=4 (4n+3)/0.8=(20n+15)m/s.(n=0、1、2　 …)

向右传播时，v=x/t=(4n+1)/0.2=(20n+5)m/s. 或v=λ/T=4 (4n+1)/0.8=(20n+5)m/s. (n=0、1、2　 …)

④若波速是35m/s，则波在0.2s内传播的距离为x=vt=35×0.2m=7m=1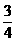λ，所以波向左传播。

⑤若0.2s小于一个周期，说明波在0.2s内传播的距离小于一个波长。则：

向左传播时，传播的距离x=3λ/4=3m；传播的时间t=3T/4得：周期T=0.267s；波速v=15m/s.向右传播时，传播的距离为λ/4=1m；传播的时间t=T/4得：周期T=0.8s；波速v =5m/s.

点评：做此类问题的选择题时，可用答案代入检验法。

[例5]如图所示，一列简谐横波在t₁时刻的波形，如图甲所示，质点P在该时刻的振动速度为v，t₂时刻质点P的振动速度与t₁时刻的速度大小相等，方向相同；t₃时刻质点P的速度与t₁时刻的速度大小相等，方向相反．若t₂－t₁＝t₃-t₂＝0．2秒，求这列波的传播速度．

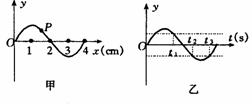　 解析：从振动模型分析，若质点P从t₁时刻开始向平衡位置方向振动，在一个周期内，从t₁时刻到t₂时刻，从t₂时刻到t₃时刻，对应的振动图象如图乙所示．考虑到振动的周期性，则有：　 t₂-t₁＝(n+1／4)T　　　 n＝0，1，2……

　 周期为：T=(t₂一t₁)／(n十1/4)　 n＝0，1，2……

　 由公式：v＝λ／T　 得出速度v的通解为：

　v＝20(n+l／4) n=0，1，2……方向向左．

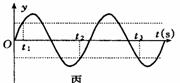　 若质点 P从 t₁时刻开始背离平衡位置方向振动，在一个周期内，从t₁时刻到t2时刻，从t₂时刻到t₃时刻，对应的振动图象如图丙所示．考虑到振动的周期性，则有：

　 t₂-t₁＝(n+3／4)T　　　 n＝0，1，2……

　 周期为：T=(t₂一t₁)／(n十3/4)　 n＝0，1，2……

　 由公式：v＝λ／T　 得出速度v的通解为： v＝20(n+3／4) n=0，1，2……方向向右．

　 答案：v＝20(n+l／4)(n＝0，1，2……)　　 方向向左．

　　 或v＝ 20( n+ 3／4)( n＝ 0，1，2，……)方向向右

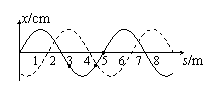[例6]已知在t₁时刻简谐横波的波形如图中实线所示；在时刻t₂该波的波形如图中虚线所示。t₂-t₁ = 0.02s来求：⑴该波可能的传播速度。

⑵若已知T< t₂-t₁<2T，且图中P质点在t₁时刻的瞬时速度方向向上，求可能的波速。

⑶若0.01s<T<0.02s，且从t₁时刻起，图中Q质点比R质点先回到平衡位置，求可能的波速。

解：⑴如果这列简谐横波是向右传播的，在t₂-t₁内波形向右匀速传播了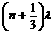，所以波速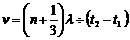=100(3n+1)m/s (n=0,1,2,…)；同理可得若该波是向左传播的，可能的波速v=100(3n+2)m/s　 (n=0,1,2,…)

　　 ⑵P质点速度向上，说明波向左传播，T< t₂-t₁ <2T，说明这段时间内波只可能是向左传播了5/3个波长，所以速度是唯一的：v=500m/s

　　 ⑶“Q比R先回到平衡位置”，说明波只能是向右传播的，而0.01s<T<0.02s，也就是T<0.02s<2T，所以这段时间内波只可能向右传播了4/3个波长，解也是唯一的：v=400m/s

[例7]一列横波沿直线在空间传播，某一时刻直线上相距为d的M、N两点均处在平衡位置，且M、N之间仅有一个波峰，若经过时间t，N质点恰好到达波峰位置，则该列波可能的波速是多少？

分析与解：本题没有给定波的传播方向，仅告诉我们在某一时刻M、N两点均处在平衡位置，且M、N之间仅有一个波峰．由此我们可以推想，处在直线MN上的各个质点在该时刻相对平衡位置的位移可能会有以下四种情况，即波的图像有以下四种图形(如图中A、B、C、D图，各图中均为左端为M，右端为N)：若波的传播方向由M到N，那么：

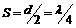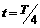　 在A图中，经过时间t，N恰好到达波峰，说明时间t内波向右前进的距离，且，所以波速．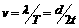

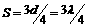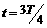　　 在B图中，经过时间t，波峰传到N点，则波在时间t内向右前进的距离，且，所以波速．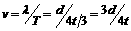

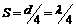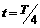　　 在C图中，经过时间t，波向右前进的距离，且，所以波速．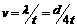

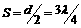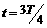　　 在D图中，经过时间t，波向右前进的距离，且，所以波速．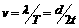

　　 若波的传播方向从N到M，那么：

　　 在A图中，质点N此时要向下振动，经过时间t，N到达波峰，则时间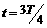，在时间t内波向左前进的距离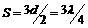，所以波速．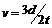

　　 在B图中，经过时间t， N到达波峰，则时间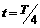，在此时间内波向左前进的距离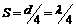，所以波速．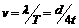

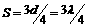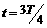　　 在C图中，波在时间t内向左前进的距离，且，所以波速．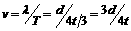

　　 在D图中，质点N经过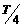变为波峰，所以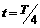，在时间t内波向左前进的距离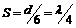，所以波速．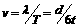

所以该列波可能的波速有五种、、、、．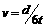

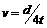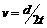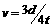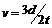　其实上述解决问题的方法过于程序化，如果能够判断出八种情况下该时刻波形图上的波峰在传播方向上到N点的距离S，波速v就等于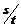．例如：最后一种情况中，波峰在传播方向上到N点的距离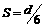，所以波速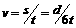．其它情况读者可自行解决．

4.介质中两质点间的距离与波长关系未定

　　 在波的传播方向上，如果两个质点间的距离不确定，就会形成多解，解题时若不能联想到所有可能情况，易出现漏解．

3.波的双向性

　　 双向性是指波沿正负方向传播时，若正、负两方向的传播时间之和等于周期的整数倍，则沿正负两方向传播的某一时刻波形相同．