6、关于加速度的概念，以下说法中正确的是：

A．物体运动加速度的方向与初速度方向相同，物体的运动速度将增大

B．物体运动加速度的大小表示了速度变化的大小

C．加速度的正负表示了物体运动的方向

D．做匀变速直线运动的物体速度增大的过程中，它的加速废一定为正值

5、某质点作直线运动，速度随时间的变化的关系式为v =(2t + 4)m/s ，则对这个质点运动描述，正确的是(　　　 )

A、初速度为4 m/s　　　　　　　　　　　　 B、加速度为2 m/s²

C、在3s末，瞬时速度为10 m/s　　　　　　 D、前3s内，位移为30 m

4、关于自由落体运动 ，正确的说法是(　　　 )

A、自由落体运动是一种匀变速运动

B、自由落体的快慢与物体质量的大小有关

C、在地球表面上各处，物体自由落体运动的加速度大小相等

D、在地球表面上经度较大处，物体自由落体运动的加速度较大

3、一列火车匀减速进站，停靠一段时间后又匀加速(同方向)出站。在如图所示的四个v-t图象中，正确描述了火车运动情况的是(　　 )

0

2、物体从静止开始作匀加速直线运动，第3 s时间内通过的位移为3m ，则(　　　 )

A、物体前3s内通过的位移是6m

B、物体第3s末的速度为3.6m/s

C、物体前3s内平均速度为2m/s

D、物体第3s内的平均速度为3m/s

1、下列关于质点的说法，正确的是(　　　 )

A、只有小的物体才能看作质点

B、大的物体也可以看作质点

C、任何物体，在一定条件下都可以看作质点

D、任何物体，在任何条件下都可以看作质点

3．弹性碰撞

题目中出现：“碰撞过程中机械能不损失”．这实际就是弹性碰撞． 设两小球质量分别为m₁、m₂，碰撞前后速度为v₁、v₂、v₁^/、v₂^/，碰撞过程无机械能损失，求碰后二者的速度．

　　 根据动量守恒　　 m₁ v₁+m₂ v₂＝m₁ v₁^/+m₂ v₂^/ ……①

　　 根据机械能守恒　　 ½m₁ v₁²十½m₂v₂²= ½m₁ v₁^/2十½m₂ v₂^/2 ……②

　　 由①②得v₁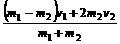^/= ，v₂^/=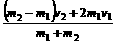

　　 仔细观察v₁^/、v₂^/结果很容易记忆,　　 当v₂=0时v₁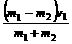^/= ，v₂^/=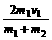

　　 ①当v₂=0时；m₁=m₂ 　时v₁^/=0，v₂^/=v₁　　 这就是我们经常说的交换速度、动量和能量．

②m₁＞＞m₂，v^/₁=v₁，v₂^/=2v₁．碰后m₁几乎未变，仍按原来速度运动，质量小的物体将以m₁的速度的两倍向前运动。

③m₁《m₂，v^/_l=一v₁，v₂^/=0．　　 碰后m₁被按原来速率弹回，m₂几乎未动。

[例1]试说明完全非弹性碰撞中机械能损失最多．

解析：前面已经说过，碰后二者一起以共同速度运动的碰撞为完全非弹性碰撞．

设两物体质量分别为m₁、m₂，速度碰前v₁、v₂，碰后v₁^/、v₂^/

由动量守恒：m₁v₁+m₂v₂＝m₁v₁^/十m₂v₂^/……①

损失机械能：Q=½m₁v₁²+½m₂v₂²－½ m₁ v₁^/2－½ m₂ v₂^/2 ……②

由①得　 m₁v₁+m₂v₁－m₂v₁+m₂v₂＝m₁v₁^/十m₂v₁^/－m₂v₁^/+m₂v₂^/　

写成(m₁+m₂)v₁－m₂(v₁－v₂)＝(m₁十m₂)v₁^/－m₂(v₁^/－v₂^/)

即(m₁+m₂)(v₁ －v₁^/)= m₂[(v₁－v₂)－(v₁^/－v₂^/)]

于是(v₁ －v₁^/)= m₂[(v₁－v₂)－(v₁^/－v₂^/)]/ (m₁+m₂)

同理由①得m₁v₁+m₁v₂－m₁v₂+m₂v₂＝m₁v₁^/十m₁v₂^/－m₁v₂^/+m₂v₂^/

写成(m₁+m₂)v₂+m₁(v₁－v₂)＝(m₁十m₂)v₂^/+m₁(v₁^/－v₂^/)

(m₁+m₂)(v₂ －v₂^/)= m₁[(v₁^/－v₂^/)－(v₁－v₂)]

(v₂ －v₂^/)= m₁[(v₁^/－v₂^/)－(v₁－v₂)]/ (m₁+m₂)

代入②得Q=½m₁v₁²+½m₂v₂²－½ m₁v₁^/2－½ m₂v₂^/2=½m₁(v₁²－v₁^/2)+½m₂(v₂²－v₂^/2)

=½m₁(v₁－v₁^/) (v₁+v₁^/)+½m₂(v₂－v₂^/)(v₂+v₂^/)

=½m₁(v₁+v₁^/) m₂[(v₁－v₂)－(v₁^/－v₂^/)]/(m₁+m₂)+½m₂(v₂+v₂^/)m₁[(v₁^/－v₂^/)－(v₁－v₂)]/(m₁+m₂)

=[½m₁ m₂/(m₁+m₂)][ v₁²－v₁v₂+v₁v₁^/－v₂v₁^/－v₁v₁^/+v₁v₂^/－v₁^/2+v₁^/v₂^/+v₂v₁^/－v₂v₂^/－v₁v₂+v₂²+v₁^/v₂^/－v₂^/2－v₁v₂^/+v₂v₂^/]=[½m₁ m₂/(m₁+m₂)][ v₁²－v₁v₂－v₁v₂+v₂²－v₁^/2+v₁^/v₂^/+v₁^/v₂^/－v₂^/2]= [½m₁ m₂/(m₁+m₂)][(v₁－v₂)²－(v₁^/－v₂^/)²]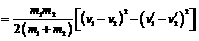……③由③式可以看出:当v₁^/= v₂^/时，损失的机械能最多．

规律方法

[例2]如图所示，一轻质弹簧两端各连接一质量均为m的滑块A和B，两滑块都置于光滑水平面上．今有质量为m/4的子弹以水平速度V射入A中不再穿出，试分析滑块B何时具有最大动能．其值为多少？

解析：对子弹和滑决A根据动量守恒定律　　　 mv/4=5mv^//4所以v^/=v/5。

　　 当弹簧被压缩后又恢复原长时，B的速度最大，具有的动能也最大，此过程动能与动量都守恒

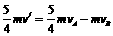
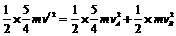
　　 由①②得：v_B=2v/9　　 所以 B的动能为E_kB=2mv²/81

答案：弹簧被压缩又恢复原长时；E_kB=2mv²/81

[例3]甲物体以动量P₁与静止在光滑水平面上的乙物体对心正碰，碰后乙物体的动量为P₂，则P₂和P₁的关系可能是(　　 )

　　 A．P₂＜P₁；　 B、P₂= P₁　　 C． P₂＞P₁；　 D．以上答案都有可能

　　 解析：此题隐含着碰撞的多种过程．若甲击穿乙物体或甲、乙两物体粘在一起匀速前进时有P₂＜P₁；若甲乙速度交换时有P₂= P₁；若甲被弹回时有P₂＞P₁；故四个答案都是可能的．而后三个答案往往漏选

　　 答案：ABCD

[例4]如图所示，在支架的圆孔上放着一个质量为M的木球，一质量为m的子弹以速度v₀从下面竖直向上击中子弹并穿出，使木球向上跳起高度为h，求子弹穿过木球后上升的高度。

　 [解析]把木球和子弹作为一个系统研究，在子弹和木球相互作用时间内，木球和子弹要受到重力作用，显然不符合动量守恒的条件。但由于子弹和木球间的作用力(内力)远大于它们的重力(外力)，可以忽略重力作用而认为系统动量守恒。

　　 设子弹刚穿过木球时，子弹的速度为v₁，木球的速度为v₂，竖直向上为正方向。

　　 对系统，据动量守恒：mv=mv₁+Mv₂……①

木球获得速度v₂后，上升的过程机械能守恒：½Mv₂²=Mgh……②

两式联立得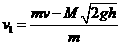

子弹射穿木球后的上升过程机械能守恒：½mv₁²=mgH，将v₁代入得子弹上升的最大高度：

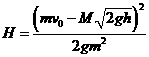
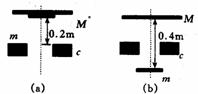[例5]有两块大小不同的圆形薄板(厚度不计)质量分别为M和m，半径分别为R和r，两板之间用一根长为0．4m的轻绳相连结．开始时，两板水平放置并叠合在一起，静止于高度为0．2m处如图(a)所示．然后自由下落到一固定支架C上，支架上有一半径为R^/(r＜R^/＜R＝的圆孔，圆孔与两薄板中心在圆板中心轴线上，木板与支架发生没有机械能损失的碰撞，碰撞后，两板即分离，直到轻绳绷紧．在轻绳绷紧瞬间，两物体具有共同速度V，如图4一22(b)所示．问：　　

(l)若M=m，则v值为多大．

　　 (2)若M/m=k，试讨论v的方向与k值间的关系．

解析：M、m与固定支架碰撞前的自由下落，所以v₀²=2gh　 v₀=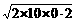=2 m／s

碰撞后，M原速返回向上作初达v₀的匀减速运动，m作初速为v₀向下匀加速运动．

设绳刚要绷直时，M的速度为v₁，上升的高度为h₁，m的速度为v₂，下降的高度为h₂，经历时间为t，则：

v₁＝v₀一gt　 …………①　　 v₁²＝v₀²一2g h₁ ……②　　 v₂＝v₀+gt………③　　

v₂²＝v₀²一2g h₂ …………④　　 又h_l+h₂=0．4…………⑤

　　 由上五式解得：v₂=3 m/s，　　 v₁=1m/s

在绳绷紧瞬间，时间极短，重力的冲量忽略不计，则M与m组成的系统动量守恒．设向下为正．则

　mv₂－Mv₁=(M+m)v，　　 即 v=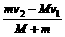　　

　　 (1)当M＝m时，v＝1m/s　　 (2)当M/m＝k时．V=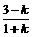

　讨论：k＜3时，v＞0两板向下运动，　 k＞3时，v＜0 两板向上运动，　 k＝3时，v＝0两板瞬时静止

[例6]如图所示，一辆质量M=2 kg的平板车左端放有质量m=3 kg的小滑块，滑块与平板车之间的动摩擦因数µ=0.4，开始时平板车和滑块共同以v₀=2m/s的速度在光滑水平面上向右运动，并与竖直墙壁发生碰撞，设碰撞时间极短且碰撞后平板车速度大小保持不变，但方向与原来相反．平板车足够长，以至滑块不会滑到平板车右端．(取g＝10 m/s²)求：

(1)平板车第一次与墙壁碰撞后向左运动的最大距离；

　(2)平板车第二次与墙壁碰撞前瞬间的速度v₂；

　(3)若滑块始终不会滑到平板车右端，平板车至少多长．

解析:平板车第一次与竖直墙壁发生碰撞后速度大小保持不变，但方向与原来相反．在此过程中，由于时间极短，故滑块m的速度与其在车上的位置均未发生变化．此外，由于相对运动，滑块m和平板车间将产生摩擦力，两者均做匀减速运动，由于平板车质量小，故其速度减为0时，滑块m仍具有向右的不为0的速度，此时起，滑块m继续减速，而平板车反向加速一段时间后，滑块M和平板车将达到共同速度，

一起向右运动，与竖直墙壁发生第二次碰撞……

(1)设平板车第一次碰墙壁后，向左移动s，速度减为0.(由于系统总动量向右，平板车速度为0时，滑块还具有向右的速度)．

　　 根据动能定理有：一½µmgs₁=0一½Mv₀²

代入数据得：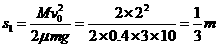

(2)假如平板车在第二次碰墙前还未和滑块相对静止，那么其速度的大小肯定还是2 m/s，滑块的速度则大于2 m/s，方向均向右，这显然不符合动量守恒定律．所以平板车在第二次碰墙前肯定已和滑块具有共同速度v₂.此即平板车碰墙瞬间的速度mv₀一Mv₀＝(M+m)v₂，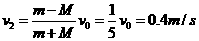

(3)平板车与墙壁第一次碰撞后到滑块与平板车又达到共同速度v前的过程，可用图(a) (b) (c)表示．图(a)为平板车与墙碰撞后瞬间滑块与平板车的位置，图(b)为平板车到达最左端时两者的位置，图(c)为平板车与滑块再次达到共同速度时两者的位置．在此过程中滑块动能减少等于摩擦力对滑块所做功µmgs^/，平板车动能减少等于摩擦力对平板车所做功µmgs^//(平板车从B到A再回到B的过程中摩擦力做功为0)，其中s' ,s"分别为滑块和平板车的位移．滑块和平板车动能总减少为µmgL，其中L＝s^/+s^//为滑块相对平板车的位移．此后，平板车与墙壁发生多次碰撞，每次情况与此类似，最后停在墙边．设滑块相对平板车总位移为L,则有：½(M+m)v₀²=µmgL,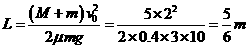

L即为平板车的最短长度．

2．一般的碰撞过程中，系统的总动能要有所减少，若总动能的损失很小，可以略去不计，这种碰憧叫做弹性碰撞．其特点是物体在碰撞过程中发生的形变完全恢复，不存在势能的储存，物体系统碰撞前后的总动能相等。若两物体碰后粘合在一起，这种碰撞动能损失最多，叫做完全非弹性碰撞．其特点是发生的形变不恢复，相碰后两物体不分开，且以同一速度运动，机械能损失显著。在碰撞的一般情况下系统动能都不会增加(有其他形式的能转化为机械能的除外，如爆炸过程)，这也常是判断一些结论是否成立的依据．

1．碰撞指的是物体间相互作用持续时间很短，而物体间相互作用力很大的现象．

在碰撞现象中，一般都满足内力远大于外力，故可以用动量守恒定律处理碰撞问题．按碰撞前后物体的动量是否在一条直线上有正碰和斜碰之分，中学物理只研究正碰的情况．

2、洛仑兹力的多解问题

(1)带电粒子电性不确定形成多解．

带电粒子可能带正电荷，也可能带负电荷，在相同的初速度下，正负粒子在磁场中运动轨迹不同，导致双解．

(2)磁场方向不确定形成多解．

若只告知磁感应强度大小，而未说明磁感应强度方向，则应考虑因磁场方向不确定而导致的多解．

(3)临界状态不惟一形成多解．

带电粒子在洛伦兹力作用下飞越有界磁场时，它可能穿过去，也可能偏转180⁰从入射界面这边反向飞出．另在光滑水平桌面上，一绝缘轻绳拉着一带电小球在匀强磁场中做匀速圆周运动，若绳突然断后，小球可能运动状态也因小球带电电性，绳中有无拉力造成多解．

(4)运动的重复性形成多解．

　　 如带电粒子在部分是电场，部分是磁场空间运动时，往往具有往复性，因而形成多解．

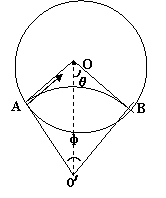
[例8]如图所示，一半径为R的绝缘圆筒中有沿轴线方向的匀强磁场，磁感应强度为B，一质量为m，带电荷量为q的正粒子(不计重力)以速度为v从筒壁的A孔沿半径方向进入筒内，设粒子和筒壁的碰撞无电荷量和能量的损失，那么要使粒子与筒壁连续碰撞，绕筒壁一周后恰好又从A孔射出，问：

(1)磁感应强度B的大小必须满足什么条件？

(2)粒子在筒中运动的时间为多少？

解析:(1)粒子射入圆筒后受洛仑兹力的作用而发生偏转,设第一次与B点碰撞,撞后速度方向又指向O点,设粒子碰撞n-1次后再从A点射出,则其运动轨迹是n段相等的弧长.

设第一段圆弧的圆心为O^/,半径为r,则θ=2π/2n=π/n.,由几何关系得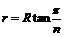,又由r=mv/Bq,联立得: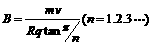

(2)粒子运动的周期为:T=2πm/qB,将B代入得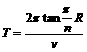

弧AB所对的圆心角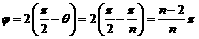

粒子由A到B所用的时间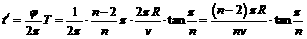　 (n=3.4.5……)

故粒子运动的总时间为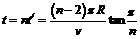　 (n=3.4.5……)

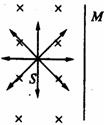[例9]S为电子源，它只能在如图(l)所示纸面上的360⁰范围内发射速率相同，质量为m，电量为e的电子，MN是一块竖直挡板，与S的水平距离OS=L，挡板左侧充满垂直纸面向里的匀强磁场，磁感强度为B．

(l)要使S发射的电子能到达挡板，则发射电子的速度至少多大？

(2)若S发射电子的速度为eBL／m时，挡板被电子击中范围多大？(要求指明S在哪个范围内发射的电子可以击中挡板，并在图中画出能击中挡板距O上下最远的电子的运动轨道)

[解析](l)电子在磁场中所受洛仑较为提供向心力qBV= mV²/r

　 当r= L/2时，速度v最小，　 由①、②可得，V=eBL／2m

　 (2)若S发射电子速率V^/=eBL／m，由eV^/B=mV^/2/r^/　　 可得：r^/=L

　 由左手定则知，电子沿SO发射时，刚好到达板上的b点，且OB= r^/= L，由SO逆时针转180⁰的范围内发射的电子均能击中挡板，落点由b→O→a→b^/→a，其中沿SO^/发射的电并击中挡板上的a点，且aO=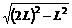=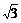L．由上分析可知，挡板能被电子击中的范围由a→b，其高度h=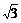L+L=(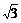十l)L，击中a、b两点的电子轨迹，如图(2)所示．

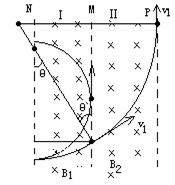
[例10]M、N、P为很长的平行边界面，M、N与M、P间距分别为L₁、L₂，其间分别有磁感应强度为B₁和B₂的匀强磁场区，Ⅰ和Ⅱ磁场方向垂直纸面向里，B₁≠B₂，有一带正电粒子的电量为q，质量为m，以大小为v的速度垂直边界M及磁场方向射入MN间的磁场区域，讨论粒子初速度v应满足什么条件才可穿过两个磁场区域(不计粒子的重力)。

解析:先讨论粒子穿出B₁的条件：

设粒子以某一速度v在磁场B₁中运动的圆轨迹刚好与M

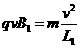
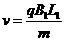
相切，此时轨迹半径刚好为L₁，由　　　　　　 得：　 　　　　

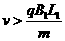
由此可得使粒子能穿出B₁的条件是：　　　　 。

再讨论粒子穿出B₂条件：

又设粒子以某一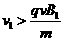的速度穿出了B₁后在B₂中穿过

时其圆轨迹又刚好与P相切，如图所示，粒子在B₁中的运动轨迹所对的圆心角为θ，那么：

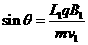
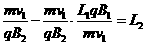，粒子在B₂运动的轨迹半径为：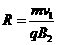

由几何知识得：R－Rsinθ=L₂ 所以有：　　　　　　　　　　　

解得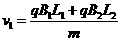：，所以当粒子的速度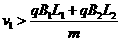时就可以穿出B₁和B₂。