
题目列表(包括答案和解析)
4.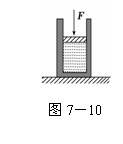 如图7-10所示,一定质量的理想气体密封在绝热(即与外界不发生热交换)
如图7-10所示,一定质量的理想气体密封在绝热(即与外界不发生热交换)
容器中,容器内装有一可以活动的绝热活塞.今对活塞施以一竖直向下的压
力F,使活塞缓慢向下移动一段距离后,气体的体积减小.若忽略活塞与容
器壁间的摩擦力,则被密封的气体( )
A.温度升高,压强增大,内能减少
B.温度降低,压强增大,内能减少
C.温度升高,压强增大,内能增加
D.温度降低,压强减小,内能增加
解析:对理想气体绝热压缩时,外界对气体做功,由热力学第一定律得,气体的内能增加,温度升高,又因气体体积减小,分子密度增大,温度升高,分子平均动能增大,故气体的压强增大,C对.
答案:C
3.外力对气体做功100 J,气体向外放热20 J,在这个过程中气体的内能________(填“增加”或“减少”),其改变量是________ J.
答案:增加 80
2.(1)2009年9月10日,美国宇航局新一代运载火箭“战神1号”通过了重要的发动机点火试验,取得圆满成功.这次点火试验投入达7 500万美元,持续了大约123秒.点火试验产生了大约2 200万马力的动力,温度约为4 500华氏度(2 480摄氏度),耗费了大量燃料.下列有关能量的说法正确的是( )
A.燃料燃烧后,能量就消失了,说明能量不守恒
B.燃料燃烧后,化学能转化为内能
C.燃料燃烧后的内能不可能再转化为化学能
D.燃料燃烧后的内能在一定条件下可能转化为化学能
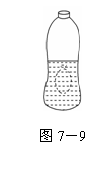 (2)如图7-9是某研究小组为了探究“鱼鳔的作用”所制作的装置.具体制作方法
(2)如图7-9是某研究小组为了探究“鱼鳔的作用”所制作的装置.具体制作方法
如下:在大号“可乐瓶”中注入半瓶水,在一个小气球中放入几枚硬币并充入少量
空气(忽略气体的分子势能),将其装入“可乐瓶”中.通过在水中放盐改变水的密
度后,使气球恰好悬浮于水中,并拧紧瓶盖.设初始时瓶中气体、水及外界大气的
温度相同.当用手挤压“可乐瓶”的上半部分时,下列说法正确的是( )
A.快速挤压时,瓶内气体压强变大
B.快速挤压时,瓶内气体温度不变
C.快速挤压时,瓶内气体体积不变
D.缓慢挤压时,气球下降
解析:(1)根据能量守恒定律可得,A项错误,B项正确.根据热力学第二定律可得,C项正确,D项错误.
(2)快速挤压气体时,外界对它做功,来不及热传递,由W+Q=ΔU,内能增大,温度上升,体积变小,瓶内压强变大,则A项对B、C两项错;缓慢挤压时,温度不变,体积变小,瓶内压强变大,对气球来说,压强也增大,温度不变,体积必然减小,则重力mg大于浮力ρgV气球,气球下降,则D项正确.
答案:(1)BC (2)AD
1.(2010·重庆卷,15)给旱区送水的消防车停于水平地面,在缓慢放水过程中,若车胎不漏气,胎内气体温度不变、不计分子间势能,则胎内气体( )
A.从外界吸热 B.对外界做负功
C.分子平均动能减小 D.内能增加
解析:选胎内气体为研究对象.由于气体温度不变,气体状态变化遵循玻意耳定律.放水前气体的压强大,在放水过程中,气体的压强逐渐减小,体积增大,气体对外界做正功,B错误.由热力学第一定律知ΔU=W+Q,气体温度不变,分子的平均动能不变,内能不变,从外界吸收热量,A正确,C、D错误.
答案:A
10.如图3-2-20所示,两平行金属板的板长不超过0.2 m,板间的电压u随时间t变化的图线如图3-2-21所示,在金属板右侧有一左边界为MN、右边无界的匀强磁场,磁感应强度B=0.01 T,方向垂直纸面向里.现有带正电的粒子连续不断地以速度v0=105 m/s,沿两板间的中线OO′平行金属板射入电场中,磁场边界MN与中线OO′垂直.已知带电粒子的比荷=108 C/kg,粒子所受的重力和粒子间的相互作用力均忽略不计.求:
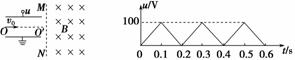
图3-2-20 图3-2-21
(1)在每个粒子通过电场区域的时间内,可以把板间的电场强度看作是恒定的.试说明这种处理能够成立的理由.
(2)设t=0.1 s时刻射入电场的带电粒子恰能从平行金属板边缘射出,求该带电粒子射出电场时的速度大小.
(3)对于所有经过电场射入磁场的带电粒子,设其射入磁场的入射点和从磁场射出的出射点间的距离为d,试判断d的大小是否随时间而变化?若不变,证明你的结论;若变,求出d的变化范围.
解析:(1)带电粒子在金属板间运动时间t==2.0×10-6 s,T=0.2 s ①
得t≪T,(或t时间内金属板间电压变化ΔU≤2×10-3 V,变化很小) ②
故t时间内金属板间的电场可以认为是恒定的.
(2)t=0.1 s时刻偏转电压U=100 V
带电粒子沿两板间的中线射入电场恰从平行金属板边缘飞出电场,电场力做功
W=qU ③
由动能定理:W=mv-mv ④
代入数据可得v1=1.41×105 m/s ⑤
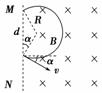
(3)设某一任意时刻射入电场的粒子速率为v,速度方向与水平方向的夹角为α,
则v= ⑥
粒子在磁场中有qvB=m ⑦
可得粒子进入磁场后,在磁场中做圆周运动的半径R=
由几何关系d=2Rcos α ⑧
可得:d==0.2 m,故d不随时间而变化.
答案:(1)带电粒子在金属板间运动时间t==2.0×10-6 s≪T=0.2 s.故t时间内金属板间的电场可以认为是恒定的.
(2)1.41×105 m/s (3)不随时间变化 d==0.2 m
9.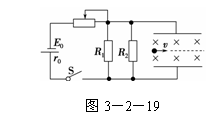 (2010·四川理综,24)如图3-2-19所示,电源电动势E0=15 V,
(2010·四川理综,24)如图3-2-19所示,电源电动势E0=15 V,
内阻r0=1 Ω,电阻R1=30 Ω,R2=60 Ω.间距d=0.2 m的两平行金属板水平放置,板间分布有垂直于纸面向里、磁感应强度B=1 T的匀强磁场.闭合开关S,板间电场视为匀强电场,将一带正电的小球以初速度v=0.1 m/s沿两板间中线水平射入板间.设滑动变阻器接入电路的阻值为Rx,忽略空气对小球的作用,取g=10 m/s2.
(1)当Rx=29 Ω时,电阻R2消耗的电功率是多大?
(2)若小球进入板间做匀速圆周运动并与板相碰,碰时速度与初速度的夹角为60°,则Rx是多少?
解析:(1)设R1和R2的并联电阻为R,有:R= ①
R2两端的电压为:U= ②
R2消耗的电功率为:P= ③
当Rx=29 Ω时,联立①②③式,代入数据,解得:
P=0.6 W ④
(2)设小球质量为m,电荷量为q,小球做匀速圆周运动时,有:qE=mg ⑤
E= ⑥
设小球做圆周运动的半径为r,有:
qvB=m ⑦
由几何关系有:r=d ⑧
联立①②⑤⑥⑦⑧式,代入数据,解得:
Rx=54 Ω. ⑨
答案:(1)0.6 W (2)54 Ω
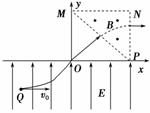
8.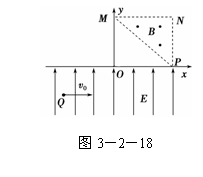 如图3-2-18所示,在平面直角坐标系xOy内,第Ⅰ象限的等
如图3-2-18所示,在平面直角坐标系xOy内,第Ⅰ象限的等
腰直角三角形MNP区域内存在垂直于坐标平面向外的匀强磁`场,y<0的区域内存在着沿y轴正方向的匀强电场.一质量为m、电荷量为q的带电粒子从电场中的Q(-2h,-h)点以速度v0水平向右射出,经坐标原点O处射入第Ⅰ象限,最后以垂直于PN的方向射出磁场.已知MN平行于x轴,N点的坐标为(2h,2h),不计粒子的重力.求:
(1)电场强度的大小E;
(2)磁感应强度的大小B;
(3)粒子在磁场中运动的时间t.
解析:(1)粒子在电场中运动过程中,由平抛运动规律及牛顿运动定律得2h=v0t
h=at2
qE=ma
解得E=.
(2)粒子到达O点时,沿y轴正方向的分速度
vy=at=·=v0
速度方向与x轴正方向的夹角α满足tan α==1,α=45°
粒子从MP的中点垂直于MP进入磁场,垂直于NP射出磁场,粒子在磁场中的速度v=v0
轨道半径R=h
由qvB=m得B=.
(3)粒子在磁场中的运动时间
t=·=.
答案:(1) (2) (3)
7.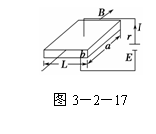 医生在做手术时,需从血库里取血,为避免感染,都是利用电磁泵从血
医生在做手术时,需从血库里取血,为避免感染,都是利用电磁泵从血
库里向外抽.如图3-2-17所示为一个电磁泵的结构图,长方形导管的前后表面绝缘,上下表面为导体,管长为L,厚为b,宽为a,内壁光滑.将导管放在垂直前后表面向里的匀强磁场中,由于充满导管的血浆中带有正负离子,将上下表面和电源接通,干路中的电流强度为I,导管的左右两侧便会产生压强差,从而将血浆抽出.若血浆的电阻率为ρ,所加电源电动势为E,内阻为r,匀强磁场的磁感应强度为B,则( )
A.此装置中血浆的等效电阻为R=
B.此装置中血浆受的安培力大小为F=BIL
C.此装置中血浆受的安培力大小为F=BIb
D.左右两侧的压强差为p=
解析:电流从上到下流过血浆时,长为b的血浆等效电阻为R=;A对;长为b的导体受安培力为F=BIb,B错C对;由压强公式得p==,D错.
答案:AC
6.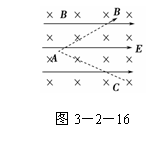 如图3-2-16所示的空间中存在着正交的匀强电场和匀强磁场,从
如图3-2-16所示的空间中存在着正交的匀强电场和匀强磁场,从
A点沿AB、AC方向绝缘地抛出两带电小球,关于小球的运动情况,
下列说法中正确的是( )
A.从AB、AC抛出的小球都可能做直线运动
B.只有沿AB抛出的小球才可能做直线运动
C.做直线运动的小球带正电,而且一定是做匀速直线运动
D.做直线运动的小球机械能守恒
解析:小球运动过程中受重力、电场力、洛伦兹力作用,注意小球做直线运动一定为匀速直线运动;正电荷沿AB才可能做直线运动,做直线运动时电场力做正功,机械能增加,B、C正确.
答案:BC
5.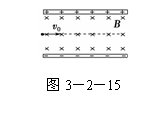 如图3-2-15所示,两平行、正对金属板水平放置,使上面金属板
如图3-2-15所示,两平行、正对金属板水平放置,使上面金属板
带上一定量正电荷,下面金属板带上等量的负电荷,再在它们之间加上垂直纸面向里的匀强磁场.一个带电粒子以初速度v0沿垂直于电场和磁场的方向从两金属板左端中央射入后向上偏转.若带电粒子所受重力可忽略不计,仍按上述方式将带电粒子射入两板间,为使其向下偏转,下列措施中一定不可行的是( )
A.仅增大带电粒子射入时的速度
B.仅增大两金属板所带的电荷量
C.仅减小粒子所带电荷量
D.仅改变粒子的电性
解析:本题意在考查带电粒子在复合场中的运动问题,解决此类问题的关键是对带电粒子进行受力分析并结合牛顿第二定律判断带电粒子的运动情况.题目中未明确带电粒子的电性,故要先做出假设,如果粒子带正电,向上偏转说明粒子所受的洛伦兹力大于电场力,所以欲使粒子向下偏转,可以增大电场即使两个极板所带电量增多,这样可使向下的电场力大于洛伦兹力,故B可行;如果粒子带负电,向上偏转说明粒子所受的洛伦兹力小于电场力,增大射入电场时的初速度可增大洛伦兹力使洛伦兹力大于电场力,故A可行;无论粒子的电性如何,改变粒子的电性可使其所受合力的方向变为反向,故D可行;粒子所受的电场力和洛伦兹力的大小关系与所带电量多少无关,故C不可行.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com