

题目列表(包括答案和解析)
4. 如图3-6所示,倾角为37°的光滑绝缘的斜面上放着M=1 kg的导
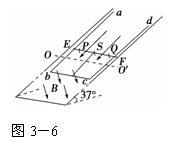
如图3-6所示,倾角为37°的光滑绝缘的斜面上放着M=1 kg的导
轨abcd,ab∥cd.另有一质量m=1 kg的金属棒EF平行bc放在导
轨上,EF下侧有绝缘的垂直于斜面的立柱P、S、Q挡住EF使之
不下滑,以OO′为界,斜面左边有一垂直于斜面向下的匀强磁
场.右边有平行于斜面向下的匀强磁场,两磁场的磁感应强度均为
B=1 T,导轨bc段长L=1 m.金属棒EF的电阻R=1.2 Ω,其余
电阻不计,金属棒与导轨间的动摩擦因数μ=0.4,开始时导轨的bc边用细线系在立柱S
上,导轨和斜面足够长,当剪断细线后,试求:
(1)导轨abcd运动的最大加速度.
(2)导轨abcd运动的最大速度.
(3)若导轨从开始运动到最大速度的过程中,流过金属棒EF的电量q=5 C,则在此过程中,系统损失的机械能是多少?(sin 37°=0.6)
解析:(1)对导轨进行受力分析有:Mgsin 37°-Ff-F安=Ma,其中F安=BIL=.对金属棒受力分析得:Ff=μN=μ,则导轨的加速度:
a=
=gsin 37°-μgcos 37°-(1-μ)
可见当v=0时,a最大;
am=gsin 37°-μgcos 37°=2.8 m/s2.
(2)当导轨达到最大速度时受力平衡即a=0,此时:
vm==5.6 m/s.
(3)设导轨下滑距离为d时达到最大速度:q=IΔt==,d=6 m
对导轨由动能定理得:Mgdsin 37°-W损=Mv
损失的机械能W损=Mgdsin 37°-Mv=20.32 J.
答案:(1)2.8 m/s2 (2)5.6 m/s (3)20.32 J
3.如图3-5所示,一质量m=2 kg的物块从水平桌面上的A点以初速度v0=4 m/s向左滑行,物块与桌面间的动摩擦因数μ=0.5,A点距弹簧所连接挡板位置B的距离xAB=0.2 m,当物块到达B点后将弹簧压缩到C点,最大压缩量为xBC=0.1 m,然后物块又被弹簧弹出,之后从桌边D点滑落.xAD=0.1 m,物块经光滑的过渡圆弧进入光滑斜面,斜面的底端与光滑的竖直圆轨道相切.桌面高0.5 m,圆轨道半径为0.4 m.(弹簧及挡板质量不计)
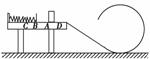
图3-5
(1)求弹簧的最大弹性势能;
(2)求物块从桌边刚滑出时的速度大小;
(3)分析物块能否达到圆轨道的顶端.
解析:(1)A→C过程中对物块由动能定理,有:
-μmgxAC+W弹=0-mv,
解得:W弹=-13 J.
故弹簧的最大弹性势能Ep=-W弹=13 J.
(2)A→C→D过程中对物块由动能定理,有:-μmg(xAC+xCD)=mv-mv,解得物块从桌边刚滑出时的速度大小为v1=3 m/s.
(3)若物块恰能达到圆轨道的顶端,则由mg=m得达到顶端时的最小速度v==2 m/s
物块从桌边到圆轨道的顶端,由机械能守恒,有:mgh+mv=2mgR+mv,解得物块在顶端的实际速度v2= m/s<2 m/s,故物块不能达到圆轨道的顶端.
答案:(1)13 J (2)3 m/s (3)不能
2.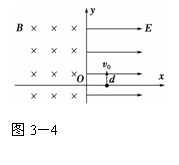 如图3-4所示,在x>0的空间中,存在沿x轴方向的匀强电场,电场强
如图3-4所示,在x>0的空间中,存在沿x轴方向的匀强电场,电场强
度E=10 N/C;在x<0的空间中,存在垂直xy平面方向的匀强磁场,磁
感应强度B=0.5 T.一带负电的粒子(比荷q/m=160 C/kg),在x=0.06 m
处的d点以v0=8 m/s的初速度沿y轴正方向开始运动;不计带电粒子的
重力.求:
(1)带电粒子开始运动后第一次通过y轴时距O点的距离.
(2)带电粒子进入磁场后经多长时间返回电场.
(3)带电粒子运动的周期.
 解析:(1)粒子在第一象限做类平抛运动(如右图所示),加速度a==1
600 m/s2,
解析:(1)粒子在第一象限做类平抛运动(如右图所示),加速度a==1
600 m/s2,
运动时间t1= = s,沿y方向的位移y=v0t= m.
(2)粒子通过y轴进入磁场时在x方向上的速度vx=at1=8 m/s,因此tan θ==
,θ=60°.粒子在第二象限以O′为圆心做匀速圆周运动,圆弧所对的圆心角为2θ
=120°,运动时间t2=T=·= s.
(3)粒子从磁场返回电场后的运动是此前由电场进入磁场运动的逆运动,经时间t3=t1,粒子的速度变为v0,此后重复前面的运动.可见,粒子在电、磁场中的运动具有周期性,其周期T=t1+t2+t3=s.
答案:(1) m (2) s (3)s
1.航模兴趣小组设计出一架遥控飞行器,其质量m=2 kg,动力系统提供的恒定升力F=28
N.试飞时,飞行器从地面由静止开始竖直上升.设飞行器飞行时所受的阻力大小不变,g取10 m/s2.
(1)第一次试飞,飞行器飞行t1=8 s时到达高度H=64 m.求飞行器所受阻力Ff的大小;
(2)第二次试飞,飞行器飞行t2=6 s时遥控器出现故障,飞行器立即失去升力,求飞行器能达到的最大高度h;
(3)为了使飞行器不致坠落到地面,求飞行器从开始下落到恢复升力的最长时间t3.
解析:(1)第一次飞行中,设加速度为a1,由匀加速运动得
H=a1t
由牛顿第二定律F-mg-Ff=ma1
解得Ff=4 N.
(2)第二次飞行中,设失去升力时的速度为v1,此时上升的高度为h1,
由匀加速运动得h1=a1t
设失去升力后加速度为a2,上升的高度为h2
由牛顿第二定律mg+Ff=ma2
v1=a1t2
h2=
解得h=h1+h2=42 m.
(3)设失去升力下降阶段加速度为a3;恢复升力后加速度为a4,恢复升力时速度为v3
由牛顿第二定律mg-Ff=ma3
F+Ff-mg=ma4
且+=h
v3=a3t3
解得t3= s(或2.1 s).
答案:(1)4 N (2)42 m (3) s(或2.1 s)
8. (2010·课标全国,23)用对温度敏感的半导体材料制成的某热敏电阻RT,
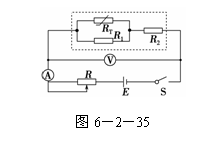
(2010·课标全国,23)用对温度敏感的半导体材料制成的某热敏电阻RT,
在给定温度范围内,其阻值随温度的变化是非线性的.某同学将RT和两
个适当的固定电阻R1、R2连成图6-2-35虚线框内所示的电路,以使
该电路的等效电阻RL的阻值随RT所处环境温度的变化近似为线性的,
且具有合适的阻值范围.为了验证这个设计,他采用伏安法测量在不同
温度下RL的阻值,测量电路如图6-2-35所示,图中的电压表内阻很
大.RL的测量结果如表1所示.
表1
|
温度t(℃) |
30.0 |
40.0 |
50.0 |
60.0 |
70.0 |
80.0 |
90.0 |
|
RL阻值(Ω) |
54.3 |
51.5 |
48.3 |
44.7 |
41.4 |
37.9 |
34.7 |
回答下列问题:
(1)根据图6-2-35所示的电路,在图6-2-36所示的实物图上连线.
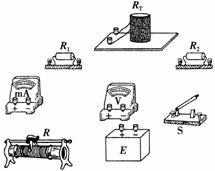
图6-2-36
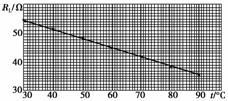
(2)为了检验RL与t之间近似为线性关系,在坐标纸上作RL-t关系图线,如图6-2-37所示:
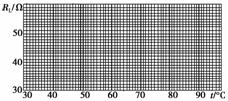
图6-2-37
(3)在某一温度下,电路中的电流表、电压表的示数如图6-2-38、6-2-39所示.电流表的读数为________,电压表的读数为________.此时等效电阻RL的阻值为________;热敏电阻所处环境的温度约为________.
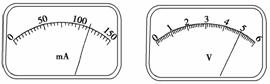
图6-2-38 图6-2-39
解析:(3)读出电压U=5.00 V、I=115 mA.RL==43.5 Ω,再由RL-t关系曲线找出RL=43.5 Ω对应的温度t=64.0℃左右,也可由表1中数据求出,具体方法是:由图象我们可以看出RL随温度均匀变化,当RL=43.5 Ω时,温度t=60℃+×(44.7-43.5)℃=64.0℃.
答案:(1)连线如图所示
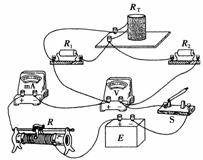
(2)RL-t关系曲线如图所示
(3)115 mA 5.00 V 43.5 Ω 64.0℃(62-66℃)
7.某同学用如图6-2-33所示的电路测量未知电阻Rx,通过调节变阻箱得到多组数据并描点得到如图6-2-34所示的图象(R为变阻箱的阻值,I为电流表的示数),其中直线a为开关S2断开时的图线,直线b为开关S2闭合时的图线,已知实验所用电流表的内阻可以忽略,则未知电阻Rx=________.
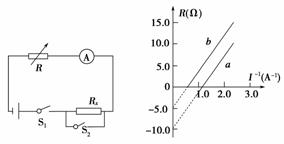
图6-2-33 图6-2-34
解析:开关S2断开时可认为电源的内阻为r+Rx,用测电源内阻的方法可以测出r+Rx的数值;开关S2闭合时测得的内阻为电源的真实内阻r,两次测量结果之差即为被测电阻Rx
开关S2断开时,由闭合电路欧姆定律E=I(R+Rx+r)得:
R=-(Rx+r),则图象a在纵轴上的截距为-(Rx+r),由图可读出:Rx+r=10.0 Ω
开关S2闭合时,由E=I(R+r)得:R=-r,则图象b在纵轴上截距为-r,由图可读出:r=5.0 Ω
Rx=10.0 Ω-5.0 Ω=5.0 Ω.
答案:5.0 Ω
6.徐老师要求同学们测出一待测电源的电动势及内阻.所给的实验器材有:待测电源E,定值电阻R1(阻值未知),电压表V(量程为3.0 V,内阻很大),电阻箱R(0-99.99 Ω),单刀单掷开关S1,单刀双掷开关S2,导线若干.
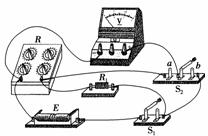
图6-2-31
(1)珊珊连接了一个如图6-2-31所示的电路,她接下来的操作是:
①拨动电阻箱旋钮,使各旋钮盘的刻度处于如图6-2-32甲所示的位置后,将S2接到a,闭合S1,记录下对应的电压表示数为2.20 V,然后断开S1;
②保持电阻箱示数不变,将S2切换到b,闭合S1,记录此时电压表的读数(电压表的示
数如图6-2-32乙所示),然后断开S1.
请你解答下列问题:

图6-2-32
图甲所示电阻箱的读数为________ Ω,图乙所示的电压表读数为________ V,由此可算出定值电阻R1的阻值为__________ Ω(计算结果保留三位有效数字).
(2)在完成上述操作后,珊珊继续以下的操作:
将S2切换到a,多次调节电阻箱,闭合S1,读出多组电阻箱的示数R和对应的电压表示数U,由测得的数据,绘出了如图丙所示的-图线.
由此可求得电源电动势E=________ V,电源内阻r=________ Ω.
答案:(1)20.00 2.80 5.45 (2)2.9 0.26
5.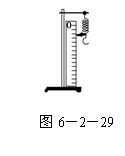 几个同学合作用如图6-2-29所示装置探究“弹力和弹簧伸长的关
几个同学合作用如图6-2-29所示装置探究“弹力和弹簧伸长的关
系”,他们先读出不挂砝码时弹簧下端指针所指的标尺刻度(图中标尺等分
刻度只是示意图),然后在弹簧下端挂上砝码,并逐个增加砝码,依次读出
指针所指的标尺刻度,所得数据列表如下(弹簧弹力始终未超过弹性限度,
重力加速度g=9.8 m/s2):
|
砝码质量m/g |
0 |
50 |
100 |
150 |
200 |
250 |
|
标尺刻度x/10-2 m |
6.00 |
8.02 |
10.00 |
13.12 |
14.10 |
15.92 |
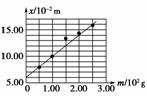
(1)根据所测数据,在图6-2-30所示的坐标纸上作出弹簧指针所指的标尺刻度x与砝码质量m的关系曲线.
(2)根据作出的关系曲线,可以求得这种规格弹簧的劲度系数为________ N/m(结果保留三位有效数字).
(3)从图6-2-30可看出,弹簧不挂砝码时,刻度尺的“0”刻度与弹簧的上端没有对齐,这对准确测出劲度系数是否有影响?________(填“有影响”或“无影响”).
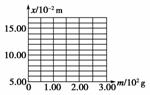
图6-2-30
解析:(1)根据表格中的数据,利用描点作图法作出图象.因13.12×10-2 m的点偏离直线太远应舍去.(2)根据第(1)问所得图象,结合胡克定律可知,求出图象的斜率的倒数,就是弹簧的劲度系数k=,做题时要注意单位的换算.(3)求弹簧的劲度系数时,需要用到的是弹簧长度的差值,与刻度尺的“0”刻度和弹簧的上端有没有对齐无关,对实验结果没有影响.
答案:(1)如图所示 (2)24.5(24.5-25.0均可) (3)无影响
4.某实验小组设计了如图6-2-28(a)所示的实验装置研究加速度和力的关系.
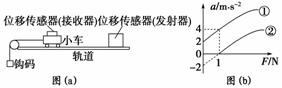
图6-2-28
(1)在该实验中必须采用控制变量法,应保持________不变,用钩码所受的重力作为_ _______,用DIS测小车的加速度.通过改变钩码的数量,多次重复测量,可得小车运动的加速度a和所受拉力F的关系图象.在轨道水平和倾斜的两种情况下分别做了实验,得到了两条a-F图线,如图6-2-28(b)所示.
(2)图线________(选填“①”或“②”)是在轨道右侧抬高成为斜面情况下得到的.
(3)随着钩码的数量增大到一定程度时图6-2-28(b)中的图线明显偏离直线,造成此误差的主要原因是( )
A.小车与轨道之间存在摩擦
B.导轨保持了水平状态
C.所挂钩码的总质量太大
D.所用小车的质量太大
(4)小车和位移传感器发射部分的总质量m=________ kg;滑块和轨道间的动摩擦因数μ=________(g取10 m/s2).
解析:(1)探究加速度与力和质量关系的实验方法是控制变量法,在探究加速度与力的关系的实验中是保持小车的总质量不变,用钩码所受的重力作为小车所受的拉力.
(2)轨道水平时一定受到摩擦力,②为未平衡摩擦力时的图线,所以①为轨道倾斜时的图线.
(3)设钩码总质量为m、小车质量为m1,则小车实际加速度为a=,所以图线偏离直线的原因是所挂钩码的总质量太大,选项C正确.
(4)当木板水平时,由牛顿第二定律可知a=-μg,图线②与a轴的交点表示-μg,所以动摩擦因数μ=0.2;图线与F轴的交点等于μmg,所以m=0.5 kg.
答案:(1)小车的总质量 小车所受拉力 (2)① (3)C (4)0.5 0.2
3.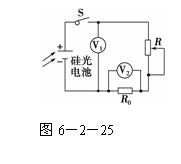 硅光电池是一种可将光能转换为电能的器件,某同学用图6-2-25所
硅光电池是一种可将光能转换为电能的器件,某同学用图6-2-25所
示电路探究影响硅光电池的内阻的因素,图中R0为已知阻值的定值电
阻,电压表视为理想电压表.
(1)请根据图用笔画线代替导线将图6-2-26中的实验器材连接成实
验电路.
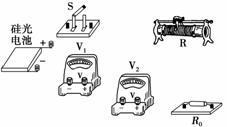
图6-2-26
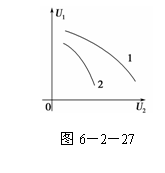 (2)实验Ⅰ:用一定强度的光照射硅光电池,调节滑动变阻器,记录两电
(2)实验Ⅰ:用一定强度的光照射硅光电池,调节滑动变阻器,记录两电
压表的读数U1和U2,作出U1-U2图象如图6-2-27曲线1.
(3)实验Ⅱ:减小实验Ⅰ中光的强度,重复实验,得到图中的曲线2.
(4)根据实验过程及图象,你能得到的结论是:
a.在光照强度一定的条件下,电池的内阻随电流的增大而________;
b.在通过相同的电流时,电池的内阻因光照强度的减弱而________.
答案:(1)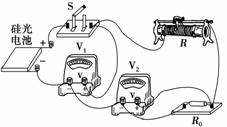
(4)a.增大 b.增大
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com