3．如图所示，质量为m的物体由静止开始从倾角分别为α、β的两个光滑固定斜面上滑下，两斜面的高度均为h，则下列叙述正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

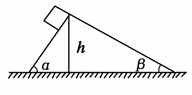
A．物体滑到斜面底端的速度相同

B．物体滑到斜面底端的速率相同

C．物体滑到斜面底端过程中重力所做的功相同

D．物体滑到斜面底端时减少的重力势能相同

[解析]　重力做功只与始末位置的高度差有关，而与具体的路径无关，所以物体沿两个不同的斜面滑下时重力所做的功相等，C、D正确；设沿倾角为α的斜面滑到斜面底端的速率为v₁，则mgh＝mv，所以v₁＝，同理，沿倾角为β的斜面滑到斜面底端时的速率v₂＝，A项错误，B项正确．

[答案]　BCD

2．有一种叫做“蹦极跳”的运动中，质量为m的游戏者身系一根长为L、弹性优良的轻质柔软的橡皮绳，从高处由静止开始下落1.5L时达到最低点，若不计空气阻力，则在弹性绳从原长到人到达最低点的过程中，以下说法正确的是　　　 　　　　　　　　　　　　　　　　　 (　)

A．速度先减小后增大

B．加速度先减小后增大

C．动能增加了mgL

D．重力势能减少了mgL

[解析]　从下落L开始一段，物体变加速下落，a减小，v增大；后来一段，物体变减速下落，a增大，v减小，故选项B正确．

[答案]　B

1．(·山东莱芜模拟)质量为m的小球从高h处由静止开始自由下落，以地面作为零势能面．当小球的动能和重力势能相等时，重力的瞬时功率为　　　　　　　　　　　　　　　　 (　)

A．2mg　　　　 B．mg

C.mg　 　　　　　　　　　　　　 D.mg

[解析]　当小球的动能和重力势能相等时，已下降的高度，速度为，所以重力的瞬时功率为mg.

[答案]　B

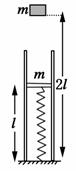
18．(·北京市海淀一模)如图所示，有一竖直固定在地面的透气圆筒，筒中有一轻弹簧，其下端固定，上端连接一质量为m的薄滑块，当滑块运动时，圆筒内壁对滑块有阻力的作用，阻力的大小恒为F_f＝mg(g为重力加速度)．在初始位置滑块静止，圆筒内壁对滑块的阻力为零，弹簧的长度为l.现有一质量也为m的物体从距地面2l处自由落下，与滑块发生碰撞，碰撞时间极短．碰撞后物体与滑块粘在一起向下运动，运动到最低点后又被弹回向上运动，滑动到刚发生碰撞位置时速度恰好为零，不计空气阻力．求

(1)物体与滑块碰撞后共同运动速度的大小；

(2)碰撞后，在滑块向下运动的最低点的过程中弹簧弹性势能的变化量．

[解析]　(1)设物体下落至与薄滑块碰撞前的速度为v₀，在此过程中机械能守恒，依据机械能守恒定律有mgl＝mv/2

解得v₀＝

设碰撞后共同速度为v，依据动量守恒定律有mv₀＝2mv

解得v＝.

(2)设物体和滑块碰撞后下滑的最大距离为x，依据动能定理，对碰撞后物体与滑块一起向下运动到返回初始位置的过程，有

－2F_fx＝0－×2mv²

设在滑块向下运动的过程中，弹簧的弹力所做的功为W，依据动能定理，对碰撞后物体与滑块一起向下运动到最低点的过程，有W+2mgx－F_fx＝0－×2mv²

解得W＝－mgl，所以弹簧弹性势能增加了mgl.

[答案]　(1)　(2)mgl

17．如图所示，光滑水平面上放置质量均为M＝2kg的甲、乙两辆小车，两车之间通过一感应开关相连(当滑块滑过感应开关时，两车自动分离)．甲车上表面光滑，乙车上表面与滑块P之间的动摩擦因数μ＝0.5.一根通过细线拴着且被压缩的轻质弹簧固定在甲车的左端，质量为m＝1kg的滑块P(可视为质点)与弹簧的右端接触但不相连，此时弹簧的弹性势能E_p＝10J，弹簧原长小于甲车长度，整个系统处于静止状态．现剪断细线，求：

(1)滑块P滑上乙车前的瞬时速度的大小．

(2)滑块P滑上乙车后最终未滑离乙车，滑块P在乙车上滑行的距离．(g＝10m/s²)

[解析]　(1)设滑块P滑上乙车前的速度为v，两小车速度为V，对整体应用动量守恒和能量关系有：

mv－2MV＝0

E_p＝+

解之得v＝4m/s，V＝1m/s

(2)设滑块P和小车乙达到的共同速度为v′，对滑块P和小车乙有mv－MV＝(m+M)v′

μmgL＝mv²+MV²－(m+M)v′²

代入数据解得L＝m

[答案]　(1)4m/s　(2)m

16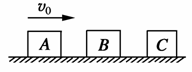．如图所示，在光滑水平面上放着A、B、C三个物块，A、B、C的质量依次是m、2m、3m.现让A物块以初速度v₀向B运动，A、B相碰后不再分开，共同向C运动；它们和C相碰后也不再分开，ABC共同向右运动．求：

(1)ABC共同向右运动的速度v的大小．

(2)A、B碰撞过程中的动能损失ΔE_k.

(3)AB与C碰撞过程B物块对C物块的冲量大小I.

[解析]　(1)以A、B、C整体为对象，全过程应用动量守恒定律：

mv₀＝(m+2m+3m)v

得ABC共同向右运动的速度v＝.

(2)设A、B碰撞后的速度为v′，根据动量守恒有

mv₀＝(m+2m)v′

动能损失ΔE_k＝mv－(m+2m)v′²

得ΔE_k＝mv.

(3)以C为研究对象，AB与C碰撞过程应用动量定理，B物块对C物块的冲量等于C物块的动量变化

I＝3mv＝mv₀.

[答案]　(1)　(2)mv　(3)mv₀

15．“蹦床”已成为奥运会的比赛项目．质量为m的运动员从床垫正上方h₁高处自由落下，落垫后反弹的高度为h₂，设运动员每次与床垫接触时间为t，求在运动员与床垫接触的时间内运动员对床垫的平均作用力．(空气阻力不计，重力加速度为g)

[思维点拨]　运动员的整个过程可分为三个阶段：自由下落h₁阶段，与床垫作用阶段，反弹竖直上升h₂阶段．要求运动员对床垫的平均作用力，只要以运动员为研究对象，对运动员与床垫作用过程用动量定理即可解决．

[解析]　设运动员刚接触床垫的速度大小为v₁，则离开床垫的速度大小为v₂，由机械能守恒得：

mv＝mgh₁，mv＝mgh₂，

设时间t内，床垫对运动员的平均作用力为F，取向上为正方向，由动量定理得：

(F－mg)t＝mv₂－(－mv₁)

以上三式联立可得：F＝+mg

再由牛顿第三定律得，运动员对床垫的作用力为

F′＝F＝+mg，方向竖直向下．

[答案]　+mg，方向竖直向下

[反思归纳]　这类题本身并不难，也不复杂，但一定要认真审题，一般遇到涉及力、时间和速度变化的问题时，运用动量定理解答往往比运用牛顿定律及运动学规律求解更简便．

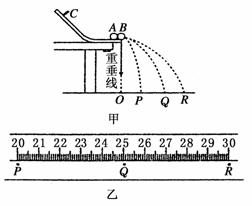
14．某同学用如图甲所示装置通过半径相同的A、B两球的碰撞来验证动量守恒定律．实验时先使A球从斜槽上某一固定位置C由静止开始滚下，落到位于水平地面的记录纸上，留下痕迹，重复上述操作10次，得到10个落点痕迹；再把B球放在水平槽上靠近槽末端的地方，让A球仍从位置C由静止开始滚下，和B球碰撞后，A、B球分别在记录纸上留下各自的落点痕迹，重复这种操作10次，得到如图乙所示的三个落地处．O点(图乙中未画出)是水平槽末端在记录纸上的垂直投影点，米尺的零点与O点对齐．

(1)观察图乙读出OP＝__________.

(2)已知m_A?m_B＝2.5?1，碰撞过程中动量守恒，则由图可以判断出Q是__________球的落地处，P是__________球的落地处．

(3)用题中的字母写出动量守恒定律的表达式_______　　　 ______________________．

[答案]　(1)20.00cm　(2)不发生碰撞时A　碰撞后A　(3)m_A·OQ＝m_A·OP+m_B·OR

13．在做验证动量守恒定律的实验时应注意的事项：

(1)入射球的质量必须__________被碰球的质量，两球的半径应__________________．

(2)安装仪器时，应使斜槽末端的切线保持__________________．并使两球的球心__________，且发生__________．

(3)入射球每次从__________________滚下．

[答案]　(1)大于　相等　(2)水平　等高　正碰　(3)同一位置

12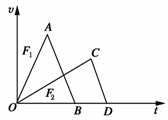．(·北京东城区质检)水平推力F₁和F₂分别作用于水平面上原来静止的等质量的a、b两物体上，作用一段时间后撤去推力，物体将继续运动一段时间停下，两物体的v-t图线如图所示，已知图中的线段AB∥CD，则　　　　　　　 　 (　)

A．F₁的冲量大于F₂的冲量

B．F₁的冲量等于F₂的冲量

C．F₁的冲量小于F₂的冲量

D．两物体受到的摩擦力大小不等

[解析]　考查动量定理．根据图象AB∥CD可知两物体在仅受摩擦力作用时的加速度相同，由于质量也相同，故受到的摩擦力也相同；对全过程应用动量定理可知推力的冲量与摩擦力的冲量大小相等，而地面对b的摩擦力作用时间较长，故力F₂的冲量较大，C正确．

[答案]　C