
题目列表(包括答案和解析)
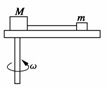
5. 如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动.P为圆周轨道的最高点.若小球通过圆周轨道最低点时的速度大小为 ,则以下判断正确的是
( )
如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动.P为圆周轨道的最高点.若小球通过圆周轨道最低点时的速度大小为 ,则以下判断正确的是
( )
A.小球不能到达P点
B.小球到达P点 时的速度小于
时的速度小于
C.小球能到达P点,但在P点不会受到轻杆的弹力
D.小球能到达P点,且在P点受到轻杆向下的弹力
[解析] 根据机械能守恒定律2mgL=mv2-mv,可求出小球在P点的速度为<,故B正确,A错误.计算出向心力F=mg,故小球在P点受到轻杆向上的弹力,故C、D均错误.
 [答案] B
[答案] B
4.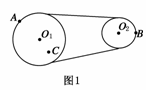 如图所示,两轮用皮带传动,皮带不打滑,图中有A、B、C三点、这三点所在处半径rA>rB=rC,则这三点的向心加速度aA、aB、aC的关系是
如图所示,两轮用皮带传动,皮带不打滑,图中有A、B、C三点、这三点所在处半径rA>rB=rC,则这三点的向心加速度aA、aB、aC的关系是  ( )
( )
A.aA=aB=aC B.aC>aA>aB
C.aC<aA<aB D.aC=aB>aA
[解析] 皮带传动且不打滑,A点与B点线速度相同,由a=有a∝;所以aA<aB,A点与C点共轴转动,角速度相同,由a=ω2r知a∝r,所以有aA>aC,可见选项C正确.
[答案] C
3.水平抛出一个物体,经时间t后物体的速度方向与水平 方向夹角为θ,重力加速度为g,则平抛物体的初速度为 ( )
方向夹角为θ,重力加速度为g,则平抛物体的初速度为 ( )
A.gtsinθ B.gtcosθ
C.gttanθ D.gtcotθ
[解析] 经时间t后物体速度的竖直分量vy=gt,故求出vx=v0=vycotθ=gtcotθ.
[答案] D
2.小船在水速较小的河中横渡,并使船头始终垂直河岸航行,到达河中间时突然上游来大水使水流速度加快,则对此小船渡河的说 法正确的是 ( )
法正确的是 ( )
A.小船要用更长的时间才能到达对岸
B.小船到对岸的时间不变,但位移将变大
C.因小船船头始终垂直河岸航行,故所用时间及位移都不会变化
D.因船速与水速关系未知,故无法确定渡河时间及位移的变化
[解析] 由运动的独立性,小船到达对岸所需的时间将不受水流速度变化的影响,选项AD错;水流速度加快,因此小船因受冲击,到达对岸的位置 偏向下游,位移将变大,故选项B对、C错.
偏向下游,位移将变大,故选项B对、C错.
[答案] B
1.关于两个运动的合成,下列说法正确的是 ( )
A.两个直线运动的合运动一定也是直线运动
B.两个匀速直线运动的合运动一定也是匀速直线运动
C.两个匀变速直线运动的合运动一定也是匀变速直线运动
D.一个匀速直线运动和一个匀变速直线运动的合运动一定是曲线运动
[解析] 可举出选项A的反例--平抛,故选项A错误;合初速度的方向与合加速度的方向不在一条直线上时是曲线运动,C错;可举出选项D的反例--竖直上抛运动,故选项D错误.
[答案] B
18.(2010·苏锡常镇四市教学调查)如图甲所示,一竖直平面内的轨道由粗糙斜面AD和光滑圆轨道DCE组成,AD与DCE相切于D点,C为圆轨道的最低点,将一小物块置于轨道ADC上离地面高为H处由静止下滑,用力传感器测出其经过C点时对轨道的压力N,改变H的大小,可测出相应的N的大小,N随H的变化关系如图乙折线PQI所示(PQ与QI两直线相连接于Q点),QI反向延长交纵轴于F点(0,5.8N),重力加速度g取10m/s2,求:

(1)小物块的质量m;
(2)圆轨道的半径及轨道DC所对应的圆心角θ;(可用角度的三角函数值表示)
(3)小物块与斜面AD间的动摩擦因数μ.
[解析] (1)如果物块只在圆轨道上运动,则由动能定理得mgH=mv2
解得v=
由向心力公式N-mg=m
得N=m+mg=H+mg
结合PQ曲线可知mg=5得m=0.5kg
(2)由图像可知=10得R=1m
cosθ==0.8,θ=37°
(3)如果物块由斜面上滑下,由动能定理得
mgH-μmgcosθ=mv2
解得mv2=2mgH-μmg(H-0.2)
由向心力公式N-mg=m得N=m+mg=H+μmg+mg
结合QI曲线知μmg+mg=5.8
解得μ=0.3.
17.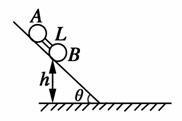 如图所示,倾角为θ的光滑斜面上放有两个质量均为m的小球A、B,两小球用一根长L的轻杆相连,下面的B球离斜面底端的高度为h,两球从静止开始下滑并从斜面进入光滑平面(不计与地面碰撞时的机械能损失).求:
如图所示,倾角为θ的光滑斜面上放有两个质量均为m的小球A、B,两小球用一根长L的轻杆相连,下面的B球离斜面底端的高度为h,两球从静止开始下滑并从斜面进入光滑平面(不计与地面碰撞时的机械能损失).求:
(1)两球在光滑平面上运动时的速度;
(2)在这过程中杆对A球所做的功;
(3)杆对A做功所处的时间段.
[解析] (1)因系统机械能守恒,所以有:
mgh+mg(h+Lsinθ)=×2mv2
∴v=.
(2)以A球为研究对象,由动能定理得:
mg(h+Lsinθ)+W=mv2
则mg(h+Lsinθ)+W=m(2gh+gLsinθ)
解得W=-mgLsinθ.
(3)从B 球与地面刚接触开始至A球也到达地面的这段时间内,杆对A球做了W的负功.
球与地面刚接触开始至A球也到达地面的这段时间内,杆对A球做了W的负功.
[答案] (1) (2)-mgLsinθ
(3)从B球与地面刚接触开始至A球也到达地面的这段时间内
16.(·黄冈质检)一种采用电力和内燃机双动力驱动的新型列车,质量为m,当它在平直的铁轨上行驶时,若只采用内燃机驱动,发动机额定功率为P1,列车能达到的最大速度为v1;在列车行驶过程中由于某种原因停在倾角为θ的坡道上,为了保证列车上坡时有足够大的动力,需改为电力驱动,此时发动机的额定功率为P2.已知列车在坡道上行驶时所受铁轨的阻力是在平直铁轨上行驶时的k倍,重力加速度为g,求列车在坡道上能达到的最大速度.
[解析] 内燃机驱动时,当列车以额定功率P1匀速行驶时速度最大,设内燃机驱动力为F1,行驶时受到的阻力为f,有
P1=F1v1 ①
F1=f ②
当列车上坡时,采用电力驱动,设其驱动力为F2,则
F2=mgsinθ+kf ③
设列车在坡道上能达到的最大速度为v2,由功率公式得
P2=F2v2 ④
由①②③④式解得v2= ⑤
15. (2010·成都市摸底测试)如图所示为某同学设计的节能运输系统.斜面轨道的倾角为37°,木箱与轨道之间的动摩擦因数μ=0.25.设计要求:木箱在轨道顶端时,自动装货装置将质量m=2kg的货物装入木箱,木箱载着货物沿轨道无初速滑下,当轻弹簧被压缩至最短时,自动装货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,接着再重复上述过程.若g取10m/s2,sin37°=0.6,cos37°=0.8.求:
(2010·成都市摸底测试)如图所示为某同学设计的节能运输系统.斜面轨道的倾角为37°,木箱与轨道之间的动摩擦因数μ=0.25.设计要求:木箱在轨道顶端时,自动装货装置将质量m=2kg的货物装入木箱,木箱载着货物沿轨道无初速滑下,当轻弹簧被压缩至最短时,自动装货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,接着再重复上述过程.若g取10m/s2,sin37°=0.6,cos37°=0.8.求:
(1)离开弹簧后,木箱沿轨道上滑的过程中的加速度大小;
(2)满足设计要求的木箱质量.
[解析] (1)设木箱质量为m′,对木箱的上滑过程,由牛顿第二定律有:
m′gsin37°+μm′gcos37°=m′a
代入数据解得:a=8m/s2
(2)设木箱沿轨道下滑的最大距离为L,弹簧被压缩至最短时的弹性势能为EP,根据能量守恒定律:货物和木箱下滑过程中有:(m′+m)gsin37°L=μ(m′+m)gcos37°L+EP
木箱上滑过程中有EP=m′gsin37°L+μm′gcos37°L
联立代入数据解得:m′=m=2kg
14.在利用重锤下落验证机械能守恒定律的实验中:
(1)某同学在实验中得到的纸带如图所示,其中A、B、C、D是打下的相邻的四个点,它们到运动起点O的距离分别为62.99cm、70.18cm、77.76cm、85.73cm.
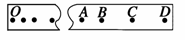
已知当地的重力加速度g=9.8m/s2,打点计时器所用电源频率为50Hz,重锤质量为1.00kg.请根据以上数据计算重锤由O点运动C点的过程中,重力势能的减少量为__________J,动能的增加量为__________J.(取三位有效数字)
(2)甲、乙、丙三名同学分别得到A、B、C三条纸带,它们前两个点间的距离分别是1.0mm、1.9mm、4.0mm.那么一定存在操作错误的同学是__________,错误原因是__________________.
[解析] (1)ΔEp=mghOC=7.62J,vC=,ΔEk=mv=7.57J.
(2)打第一个点时,速度应为零,此时前两点间距离应小于2mm,丙同学所测的前两点间距离等于4.0mm,说明打O点时纸带已经下落.
[答案] (1)7.62 7.57 (2)丙 先放纸带后接通电源
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com