
题目列表(包括答案和解析)
12.(2011东城期末)(10分)质谱仪的工作原理图如图所示,A为粒子加速器,加速电压为 ;M为速度选择器,两板间有相互垂直的匀强磁场和匀强电场,匀强磁场的磁感应强度为
;M为速度选择器,两板间有相互垂直的匀强磁场和匀强电场,匀强磁场的磁感应强度为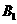 ,两板间距离为d;N为偏转分离器,内部有与纸面垂直的匀强磁场,磁感应强度为
,两板间距离为d;N为偏转分离器,内部有与纸面垂直的匀强磁场,磁感应强度为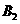 。一质量为m,电荷量为q的带正电的粒子由静止经加速器加速后,恰能通过速度选择器,进入分离器后做圆周运动,并打到感光板P上。不计重力,求:
。一质量为m,电荷量为q的带正电的粒子由静止经加速器加速后,恰能通过速度选择器,进入分离器后做圆周运动,并打到感光板P上。不计重力,求:
 (1)粒子经粒子加速器A加速后的速度
(1)粒子经粒子加速器A加速后的速度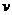 的大小及速度选择器M两板间的电压
的大小及速度选择器M两板间的电压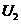 ;
;
(2)粒子在偏转分离器N的磁场中 做圆周运动的半径R;
做圆周运动的半径R;
(3)某同学提出:在其它条件不变的情况下,只减小加速电压 ,就可以使粒子在偏转分离器N的磁场中做圆周运动的半径减小。试分析他的说法是否正确。
,就可以使粒子在偏转分离器N的磁场中做圆周运动的半径减小。试分析他的说法是否正确。

(1)带电粒子在A中电场力对它做功,由动能定理
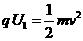
带电粒子在M中水平方向受电场力和洛仑兹力,有

可得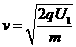
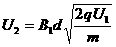 (4分)
(4分)
(2)带电粒子在N中做匀速圆周运动,洛仑兹力充当向心力
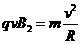
可得 (4分)
(4分)
(3)不正确。若其它条件不变,只减小加速电压U1,则粒子经加速后获得的速度减小,进入速度选择器后,粒子受到电场力和洛仑兹力大小不再相等,粒子无法通过速度选择器进入偏转分离器。 (2分)
11.(2011东城期末) 如图所示,截面为正方形空腔abcd
放置在一匀强磁场中,磁场方向垂直纸面向里。若有一束具有不同速率的电子由小孔a沿ab方向射入磁场,打在腔壁上的电子都被腔壁吸收,则由小孔c 和小孔d 射出的电子的速率之比为
;由小孔c 和d 射出的电子在磁场中运动的时间之比为
。
如图所示,截面为正方形空腔abcd
放置在一匀强磁场中,磁场方向垂直纸面向里。若有一束具有不同速率的电子由小孔a沿ab方向射入磁场,打在腔壁上的电子都被腔壁吸收,则由小孔c 和小孔d 射出的电子的速率之比为
;由小孔c 和d 射出的电子在磁场中运动的时间之比为
。
2:1;1:2
10.(2011东城期末)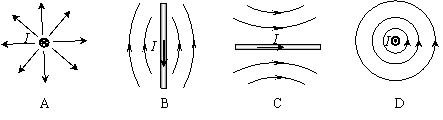 下列各图中,用带箭头的细实线表示通电直导线周围磁感线的分布情况,其中正确的是
下列各图中,用带箭头的细实线表示通电直导线周围磁感线的分布情况,其中正确的是
D
9.(2011昌平期末)(7分)如图19所示为一质谱仪的构造原理示意图,整个装置处于真空环境中,离子源N可释放出质量均为m、电荷量均为q(q>0)的离子。离子的初速度很小,可忽略不计。离子经S1、S2间电压为U的电场加速后 ,从狭缝S3进入磁感应强度大小为B、方向垂直于纸面向外的匀强磁场中,沿着半圆运动到照相底片上的P点处,测得P到S3的距离为x。求:
,从狭缝S3进入磁感应强度大小为B、方向垂直于纸面向外的匀强磁场中,沿着半圆运动到照相底片上的P点处,测得P到S3的距离为x。求:
 (1)离子经电压为U的电场加速后的速度v;
(1)离子经电压为U的电场加速后的速度v;
(2) 离子的荷质比 (q/m)
解:(1)离子经S1、S2间电压为U的电场加速,根据动能定理
qU=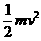 (2分)
(2分)
所以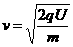 ①
(1分)
①
(1分)
(2)设离子进入磁场后做匀速圆周运动速率为v,半径为R。
洛伦兹力提供向心力 ②
(1分)
②
(1分)
又因 R=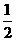 x ③
(
x ③
( 1分)
1分)
联立①②③,解得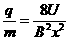 (2分)
(2分)
8.(2011昌平期末)已知氕(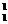 H)、氘(
H)、氘(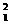 H)、氚(
H)、氚(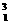 H)三个带电粒子,它们以相同的速度垂直射入同一匀强磁场中,做匀速圆周运动。则半径最大的是 ,周期最长的是
。
H)三个带电粒子,它们以相同的速度垂直射入同一匀强磁场中,做匀速圆周运动。则半径最大的是 ,周期最长的是
。
氚(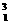 H),氚(
H),氚(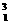 H)
H)
7.(2011昌平期末)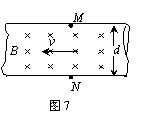 如图7所示是电磁流量计的示意图。圆管由非磁性材料制成,空间有匀强磁场。当管中的导电液体流过磁场区域时
如图7所示是电磁流量计的示意图。圆管由非磁性材料制成,空间有匀强磁场。当管中的导电液体流过磁场区域时 ,测出管壁上MN两点的电动势E,就可以知道管中液体的流量Q--单位时间内流过管道横截面的液体的体积。已知管的直径为d,磁感应强度为B,则关
,测出管壁上MN两点的电动势E,就可以知道管中液体的流量Q--单位时间内流过管道横截面的液体的体积。已知管的直径为d,磁感应强度为B,则关 于Q的表达式正确的是
于Q的表达式正确的是
A.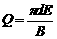 B.
B.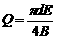
C.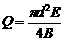 D.
D.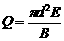
B
6.(2011昌平期末)关于磁感应强度,下列说法中正确的是
A.由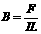 可知,B与F成正比,与IL成反比
可知,B与F成正比,与IL成反比
B.通电导线放在磁场中的某点,那点就有磁感应强度,如果将通电导线拿走,那点的磁感应强度就为零
C.通电导线不受安培力的地方一定不存在磁场,即B=0
D.磁 场中某一点的磁感应强度由磁场本身决定,其大小和方向是唯一确定的,与通电导线无关
场中某一点的磁感应强度由磁场本身决定,其大小和方向是唯一确定的,与通电导线无关
D
5.(2011昌平期末)在图2所示的四幅图中,正确标明了通电导线所受安培力F方向的是

B
3.(2011丰台一模)(18分)
 1932年美国物理学家劳伦斯发明了回旋加速器,巧妙地利用带电粒子在磁场中的运动特点,解决了粒子的加速问题。现在回旋加速器被广泛应用于科学研究和医学设备中。
1932年美国物理学家劳伦斯发明了回旋加速器,巧妙地利用带电粒子在磁场中的运动特点,解决了粒子的加速问题。现在回旋加速器被广泛应用于科学研究和医学设备中。
某型号的回旋加速器的工作原理如图甲所示,图为俯视图乙。回旋加速器的核心部分为D形盒,D形盒装在真空容器中,整个装置放在巨大的电磁铁两极之间的强大磁场中,磁场可以认为是匀强在场,且与D形盒盒面垂直。两盒间狭缝很小,带电粒子穿过的时间可以忽略不计。D形盒半径为R,磁场的磁感应强度为B。设质子从粒子源A处时入加速电场的初速度不计。质子质量为m、电荷量为+q。加速器接一定涉率高频交流电源,其电压为U。加速过程中不考虑相对论效应和重力作用。
(1)求质子第1次经过狭缝被加速后进入D形盒运动轨道的半径r1;
(2)求质子从静止开始加速到出口处所需的时间t ;
(3)如果使用这台回旋加速器加速α粒子,需要进行怎样的改动?请写出必要的分析及推理。
解析: (1) (6分)
设质子第1次经过狭缝被加速后的速度为v1
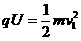 ① (2分)
① (2分)
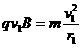 ② (2分)
② (2分)
联立①②解得: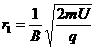 (2分)
(2分)
(2) (8分)
设质子从静止开始加速到出口处被加速了n圈,质子在出口处的速度为v
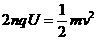 ③ (2分)
③ (2分)
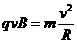 ④ (1分)
④ (1分)
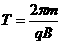 ⑤ (2分)
⑤ (2分)
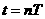 ⑥ (1分)
⑥ (1分)
联立③④⑤⑥解得 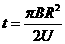 (2分)
(2分)
(3) (4分)
回旋加速器正常工作时高频电压的频率必须与粒子回旋的频率相同。设高频电压的频率为f, 则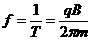
当速α粒子时α粒子的比荷为质子比荷的2倍,
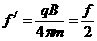 ,所以不用直接使用。
(2分)
,所以不用直接使用。
(2分)
改动方法一:让回旋磁场的磁感应强度加倍。 (2分)
改动方法二:让加速高频电压的频率减半。
4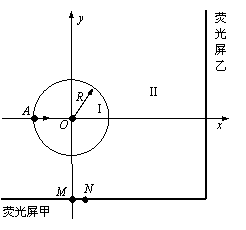 .(2011石景山一模)(20分) 如图所示,圆心在原点、半径为
.(2011石景山一模)(20分) 如图所示,圆心在原点、半径为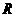 的圆将
的圆将 平面分为两个区域,在圆内区域Ⅰ(
平面分为两个区域,在圆内区域Ⅰ(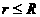 )和圆外区域Ⅱ(
)和圆外区域Ⅱ(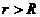 )分别存在两个匀强磁场,方向均垂直于
)分别存在两个匀强磁场,方向均垂直于 平面。垂直于
平面。垂直于 平面放置两块平面荧光屏,其中荧光屏甲平行于
平面放置两块平面荧光屏,其中荧光屏甲平行于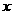 轴放置在
轴放置在
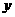 =
= 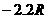 的位置,荧光屏乙平行于
的位置,荧光屏乙平行于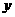 轴放置在
轴放置在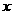 =
= 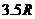 的位置。现有一束质量为
的位置。现有一束质量为 、电荷量为
、电荷量为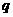 (
(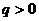 )、动能为
)、动能为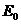 的粒子从坐标为(
的粒子从坐标为(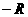 ,
, )的
)的 点沿
点沿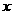 轴正方向射入区域Ⅰ,最终打在荧光屏甲上,出现亮点
轴正方向射入区域Ⅰ,最终打在荧光屏甲上,出现亮点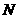 的坐标为(
的坐标为( ,
,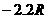 )。若撤去圆外磁场,粒子也打在荧光屏甲上,出现亮点
)。若撤去圆外磁场,粒子也打在荧光屏甲上,出现亮点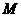 的坐标为(
的坐标为( ,
,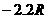 ),此时,若将荧光屏甲沿
),此时,若将荧光屏甲沿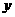 轴负方向平移,发现亮点的
轴负方向平移,发现亮点的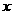 轴坐标始终保持不变。不计粒子重力影响。
轴坐标始终保持不变。不计粒子重力影响。
(1)求在区域Ⅰ和Ⅱ中粒子运动速度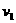 、
、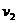 的大小;
的大小;
(2)求在区域Ⅰ和Ⅱ中磁感应强度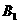 、
、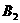 的大小和方向;
的大小和方向;
(3)若上述两个磁场保持不变,荧光屏仍在初始位置,但从 点沿
点沿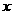 轴正方向射入区域Ⅰ的粒子束改为质量为
轴正方向射入区域Ⅰ的粒子束改为质量为 、电荷量为
、电荷量为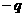 、动能为
、动能为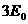 的粒子,求荧光屏上出现亮点的坐标。
的粒子,求荧光屏上出现亮点的坐标。
(1)由于在磁场中运动时洛仑兹力不做功,所以在区域Ⅰ和Ⅱ中粒子运动速度大小就是在 点入射时初始速度大小
点入射时初始速度大小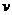 ,由
,由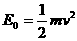 可得
可得
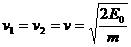 ……………………………………………(2分)
……………………………………………(2分)
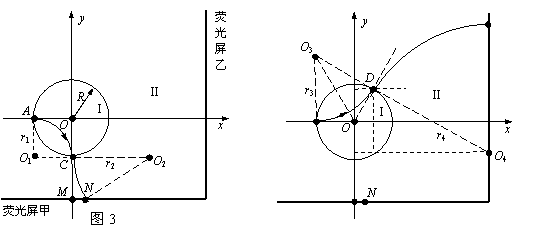 (2)粒子在区域Ⅰ中运动了四分之一圆周后,从C点沿
(2)粒子在区域Ⅰ中运动了四分之一圆周后,从C点沿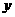 轴负方向进入区域Ⅱ的磁场。如图3所示,圆周运动的圆心是
轴负方向进入区域Ⅱ的磁场。如图3所示,圆周运动的圆心是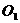 点,半径为
点,半径为
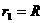 ……………………………………………………………(2分)
……………………………………………………………(2分)
由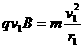 ,得
,得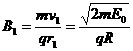 ………………………………(2分)
………………………………(2分)
方向垂直 平面向外。 ………………………………………………………(1分)
平面向外。 ………………………………………………………(1分)
粒子进入区域Ⅱ后做半径为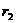 的圆周运动,由
的圆周运动,由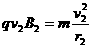 ,可得
,可得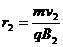 ,
,
圆周运动的圆心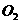 坐标为(
坐标为(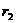 ,
,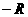 ),圆周运动轨迹方程为
),圆周运动轨迹方程为
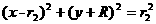
将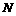 点的坐标(
点的坐标( ,
,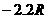 )代入上式,可得
)代入上式,可得
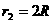 ……………………………………………………(2分)
……………………………………………………(2分)
求得:
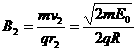 …………………………………………(2分)
…………………………………………(2分)
方向垂直 平面向里。 ……………………………………………………(1分)
平面向里。 ……………………………………………………(1分)
(3)如图4所示,粒子先在区域Ⅰ中做圆周运动。由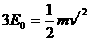 可知,运动速度为
可知,运动速度为
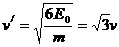
轨道半径为 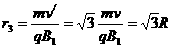 ………………………………(1分)
………………………………(1分)
由圆心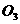 的坐标(
的坐标(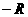 ,
,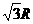 )可知,
)可知, 与
与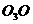 的夹角为
的夹角为 。通过分析如图的几何关系,粒子从D点穿出区域Ⅰ的速度方向与
。通过分析如图的几何关系,粒子从D点穿出区域Ⅰ的速度方向与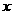 轴正方向的夹角为
轴正方向的夹角为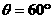 …(1分)
…(1分)
粒子进入区域Ⅱ后做圆周运动的半径为
 …………………………(2分)
…………………………(2分)
其圆心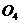 的坐标为(
的坐标为(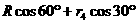 ,
,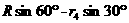 ),即(
),即(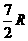 ,
,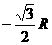 ),说明圆心
),说明圆心 恰好在荧光屏乙上。所以,亮点将出现在荧光屏乙上的P点,
恰好在荧光屏乙上。所以,亮点将出现在荧光屏乙上的P点,
其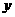 轴坐标为
轴坐标为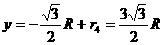 …………………………………(2分)
…………………………………(2分)
其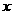 轴坐标为
轴坐标为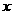 =
= 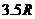 …………………………………………………(2分)
…………………………………………………(2分)
.(2011房山期末)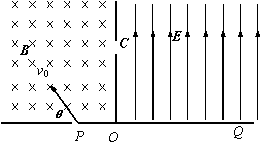 如图所示的区域中,左边为垂直纸面向里的匀强磁场,磁感应强度为 B ,右边是一个电场强度大小未知的匀强电场,其方向平行于OC且垂直于磁场方向.一个质量为m 、电荷量为-q 的带电粒子从P孔以初速度V0沿垂直于磁场方向进人匀强磁场中,初速度方向与边界线的夹角θ=600 ,粒子恰好从C孔垂直于OC射入匀强电场,最后打在Q点,已知OQ= 2 OC ,
如图所示的区域中,左边为垂直纸面向里的匀强磁场,磁感应强度为 B ,右边是一个电场强度大小未知的匀强电场,其方向平行于OC且垂直于磁场方向.一个质量为m 、电荷量为-q 的带电粒子从P孔以初速度V0沿垂直于磁场方向进人匀强磁场中,初速度方向与边界线的夹角θ=600 ,粒子恰好从C孔垂直于OC射入匀强电场,最后打在Q点,已知OQ= 2 OC ,
不计粒子的重力,求:
( l )粒子从P运动到Q所用的时间 t 。
( 2 )电场强度 E 的大小
( 3 )粒子到达Q点时的动能EkQ
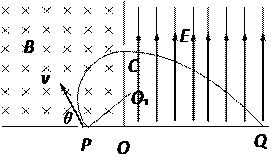 (1)画出粒子运动的轨迹如图示的三分之一圆弧
(1)画出粒子运动的轨迹如图示的三分之一圆弧
(O1为粒子在磁场中圆周运动的圆心):∠PO1 C=120°
设粒子在磁场中圆周运动的半径为r,
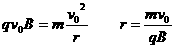 ……………………2分
……………………2分
r+rcos 60°= OC=x O C=x=3r/2 …………………………2分
粒子在磁场中圆周运动的时间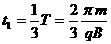 ……………………1分
……………………1分
粒子在电场中类平抛运动 O Q=2x=3r……………………1分
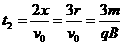 …………………………………………1分
…………………………………………1分
粒子从P运动到Q所用的时间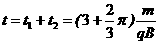 …………………………1分
…………………………1分
(2) 粒子在电 场中类平抛运动
场中类平抛运动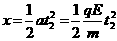 ……1分
……1分 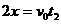 ……1分
……1分
解得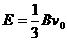 …………………1分
…………………1分
(3)由动能定理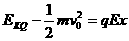 …………2分
解得粒子到达Q点时的动能为
…………2分
解得粒子到达Q点时的动能为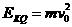 ……1
……1
6.(2011丰台期末) 爱因斯坦是近代最著名的物理学家之一,曾提出许多重要理论,为物理学的发展做出过卓越贡献。下列选项中不是他的理论的是
A. 质能方程 B. 分子电流假说
C. 光电效应方程 D. 光速不变原理
答案:B
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com