
题目列表(包括答案和解析)
10.如图(1)所示,一个足够长的“U”形金属导轨NMPQ固定在水平面内,MN、PQ两导轨间的宽为L=0.50m.一根质量为m=0.50kg的均匀金属导体棒ab静止在导轨上且接触良好,abMP恰好围成一个正方形.该轨道平面处在磁感应强度大小可以调节的竖直向上的匀强磁场中.ab棒的电阻为R=0.10 ,其他各部分电阻均不计.开始时,磁感应强度B0=0.50T
,其他各部分电阻均不计.开始时,磁感应强度B0=0.50T
(1)若保持磁感应强度B0的大小不变,从t=0时刻开始,给ab棒施加一个水平向右的拉力,使它做匀加速直线运动.此拉力T的大小随时间t变化关系如图(2)所示.求匀加速运动的加速度及ab棒与导轨间的滑动摩擦力.
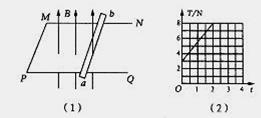 (2)若从某时刻t=0开始,调动磁感应强度的大小使其以
(2)若从某时刻t=0开始,调动磁感应强度的大小使其以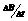 =0.20 T/s的变化率均匀增加.求经过多长时间ab棒开始滑动?此时通过ab棒的电流大小和方向如何?(ab棒与导轨间的最大静摩擦力和滑动摩擦力相等) ,
=0.20 T/s的变化率均匀增加.求经过多长时间ab棒开始滑动?此时通过ab棒的电流大小和方向如何?(ab棒与导轨间的最大静摩擦力和滑动摩擦力相等) ,
解:(1)由图象可得到拉力t的大小随时间变化的函数表达式为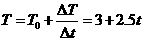
当ab棒匀加速运动时,根据牛顿第二定律有:T-f-B0Il=ma
因为I=B0lv/R
v=at 联立可解得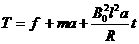
将数据代入,可解得a=4m/s2 f=1N
(2)以ab棒为研究对象,当磁培应强度均匀增大时,闭合电路中有恒定的感应电流I,以ab
棒为研究对象,它受到的安培力逐渐增大,静摩擦力也随之增大,当磁感应强度增大到ab所受安培力F与最大静摩擦力fm相等时开始滑动.
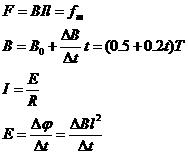
由以上各式求出,经时间t=17.5s后ab棒开始滑动,此时通过ab棒的电流大小为I=0.5A 根据楞决定律可判断出,电流的方向为从b到a.
9.如图所示,两条光滑的绝缘导轨,导轨的水平部分与圆弧部分平滑连接,两导轨间距为L,导轨的水平部分有n段相同的匀强磁场区域(图中的虚线范围),磁场方向竖直向上,磁场的磁感应强度为B,磁场的宽度为S,相邻磁场区域的间距也为S,S大于L,磁场左、右两边界均与导轨垂直。现有一质量为m,电阻为r,边长为L的正方形金属框,由圆弧导轨上某高度处静止释放,金属框滑上水平导轨,在水平导轨上滑行一段时间进入磁场区域,最终线框恰好完全通过n段磁场区域。地球表面处的重力加速度为g,感应电流的磁场可以忽略不计,求:
(1)刚开始下滑时,金属框重心离水平导轨所在平面的高度.
(2)整个过程中金属框内产生的电热.
(3)金属框完全进入第k(k<n)段磁场区域前的时刻,金属框中的电功率.

(1)设金属框在进入第一段匀强磁场区域前的速度为v0,金属框在进入和穿出第一段匀强磁场区域的过程中,线框中产生平均感应电动势为
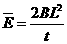 ...............................1分
...............................1分
平均电流强度为(不考虑电流方向变化)
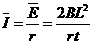 ...........................................1分
...........................................1分
由动量定理得: 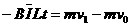 .............................1分
.............................1分
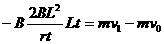
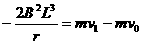
同理可得: 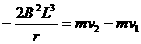
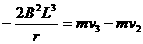
……
整个过程累计得: 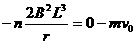 ................................1分
................................1分
解得: 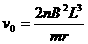 .......................................1分
.......................................1分
金属框沿斜面下滑机械能守恒:
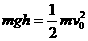 ............................................1分
............................................1分
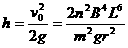 ...........................................1分
...........................................1分
(2)金属框中产生的热量Q=mgh............................. ..
Q=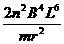 ................................................1分
................................................1分
(3)金属框穿过第(k-1)个磁场区域后,由动量定理得:
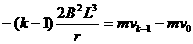 ......................2分
......................2分
金属框完全进入第k个磁场区域的过程中,由动量定理得:
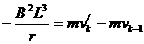 .....................1分
.....................1分
解得: 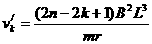 .........................1分
.........................1分
功率: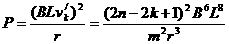 ...............................2分
...............................2分
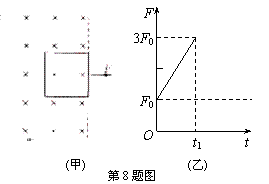
8.如图(甲)所示,一正方形金属线框放置在绝缘的光滑水平面上,并位于一竖直向下的有界匀强磁场区域内,线框的右边紧贴着磁场的边界,从t=0时开始,对线框施加一水平向右的外力F,使线框从静止开始做匀加速直线运动,在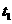 时刻穿出磁场.已知外力F随时间变化的图像如图(乙)所示,且线框的质量m、电阻R、图(乙)中的
时刻穿出磁场.已知外力F随时间变化的图像如图(乙)所示,且线框的质量m、电阻R、图(乙)中的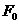 、
、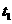 均为已知量.试求出两个与上述过程有关的电磁学物理量(即由上述已知量表达的关系式).
均为已知量.试求出两个与上述过程有关的电磁学物理量(即由上述已知量表达的关系式).
据题意知,线框运动的加速度 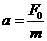 ①
①
线框离开磁场时的速度 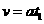 ②
②
线框的边长 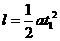 ③
③
线框离开磁场时所受到的磁场力 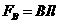 ④
④
离开磁场时线框中的感应电动势 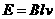 ⑤
⑤
离开磁场时线框中的感应电流 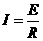 ⑥
⑥
由牛顿定律知 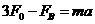 ⑦
⑦
联立求解可得 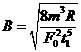 ⑧
⑧
离开磁场时线框中的感应电动势 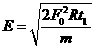 ⑨
⑨
离开磁场时线框中的感应电流 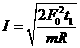 ⑩
⑩
在拉出过程中通过线框某截面的电量 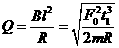 ⑾
⑾
7.一电阻为R的金属圆环,放在匀强磁场中,磁场与圆环所在平面垂直,如图(a)所示.已知通过圆环的磁通量随时间t的变化关系如图(b)所示,图中的最大磁通量φ0和变化周期T
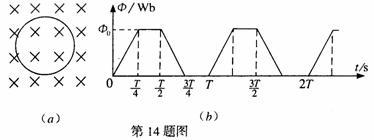 都是已知量,求
都是已知量,求
(1)在t= 0到 的时间内,通过金属圆环某横截面的电荷量q.
的时间内,通过金属圆环某横截面的电荷量q.
(2)在t= 0到t=2T的时间内,金属环所产生的电热Q.
(1)由磁通量随时间变化的图线可知在t=0到 时间内,环中的感应电动势
时间内,环中的感应电动势
E1= 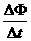 ①
①
在以上时段内,环中的电流为
I 1=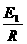 ②
②
则在这段时间内通过金属环某横截面的电量 q= I 1 t ③
联立求解得
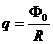 ④
④
(2)在 到
到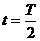 和在
和在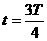 到t =T时间内,环中的感应电动势
到t =T时间内,环中的感应电动势
E 1= 0 ⑤
在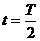 和在
和在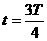 时间内,环中的感应电动势 E 3=
时间内,环中的感应电动势 E 3=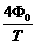 ⑥
⑥
由欧姆定律可知在以上时段内,环中的电流为 I 3 = 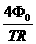 ⑦
⑦
在t=0到t=2T时间内金属环所产生的电热
Q=2(I 12 R t 3+ I 32 R t 3) ⑧
联立求解得
Q=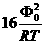 ⑨
⑨
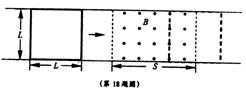
6.如图所示在水平面上有两条相互平行的光滑绝缘导轨,两导轨间距工L=1m,导轨的虚线范围内有一垂直导轨平面的匀强磁场,磁感应强度B=0.2T,磁场宽度S大于L,左、右两边界与导轨垂直.有一质量m=0.2kg,电阻 r=0.1 边长也为L正方形金属框以某一初速度,沿导轨向右进入匀强磁场.
边长也为L正方形金属框以某一初速度,沿导轨向右进入匀强磁场.
(1)若最终金属框只能有-半面积离开磁场区域,试求金属框左边刚好进入磁场时的速度.
(2)若金属框右边剐要离开磁场时,虚线范围内磁插的磁感应强度以K=0.1T/s的变化率均匀减小。为使金属框此后能匀速离开磁场,对其平行于导轨方向加一水平外力,求金属框有一半面积离开磁场区域时水平外力的大小.
解:(1)金属框左边刚好进入磁场区域时的运动速度为v,在磁场中作匀速运动.设离开磁场
运动过程的时间为t,此过程中的平均感应电动势为: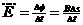 (1分)
(1分)
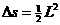 (1分)
(1分)
所受平均安培力: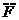 安=
安= 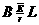 : (1分)
: (1分)
由动量定理有: -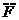 安t=0-mv (2分)
安t=0-mv (2分)
解得: v= l m/s (2分)
(2)金属框开始匀速离开磁场到有一半面积离开磁场区域的时间为:
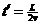 (1分)
(1分)
当线框一半面积离开磁场时,左边因切割磁感线而产生的电动势为:
E1=(B-ktˊ)Lv (2分)
因磁场变化而产生的感应电动势为:E2=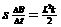 (2分)
(2分)
此回路产生逆时针方向的感应电流为:
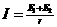 ('分)
('分)
则此时水平向右的外力大小为:F=F安=(B-ktˊ)IL (1分)
代人数据,解得: F=0.3N
5.解(1)ab棒离开磁场右边界前做匀速运动,速度为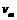 ,则有:
,则有:
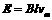 ①
①
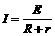 ②
②
对ab棒 F-BIl=0 ③
解得 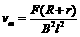 ④
④
(2)由能量守恒可得: 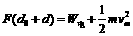 ⑤
⑤
解得: 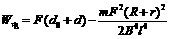 ⑥
⑥
(3)设棒刚进入磁场时速度为v
由:
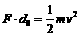 ⑦
⑦
可得:
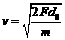 ⑧
⑧
棒在进入磁场前做匀加速直线运动,在磁场中运动可分三种情况讨论:
①若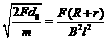 (或
(或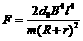 ),则棒做匀速直线运动;
),则棒做匀速直线运动;
②若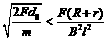 (或F>
(或F>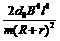 ),则棒先加速后匀速;
),则棒先加速后匀速;
③若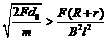 (或F<
(或F<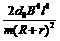 =,则棒先减速后匀速。
=,则棒先减速后匀速。
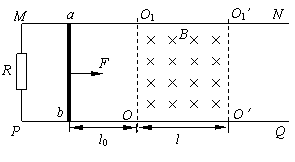
5、如图,光滑平行的水平金属导轨MN、PQ相距l,在M点和P点间接一个阻值为R的电阻,在两导轨间OO1O1′O′矩形区域内有垂直导轨平面竖直向下、宽为d的匀强磁场,磁感强度为B。一质量为m,电阻为r的导体棒ab,垂直搁在导轨上,与磁场左边界相距d0。现用一大小为F、水平向右的恒力拉ab棒,使它由静止开始运动,棒ab在离开磁场前已经做匀速直线运动(棒ab与导轨始终保持良好的接触,导轨电阻不计)。求:
(1)棒ab在离开磁场右边界时的速度;
(2)棒ab通过磁场区的过程中整个回路所消耗的电能;
(3)试分析讨论ab棒在磁场中可能的运动情况。
4.如图甲所示,光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上,两导轨间距L=0.2m,电阻R=0.4Ω,导轨上停放一质量m=0.1kg、电阻r=0.1Ω的金属杆,导轨电阻可忽略不计,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向竖直向下。现用一外力F沿水平方向拉杆,使之由静止开始运动,若理想电压表的示数U随时间t变化的关系如图乙所示。
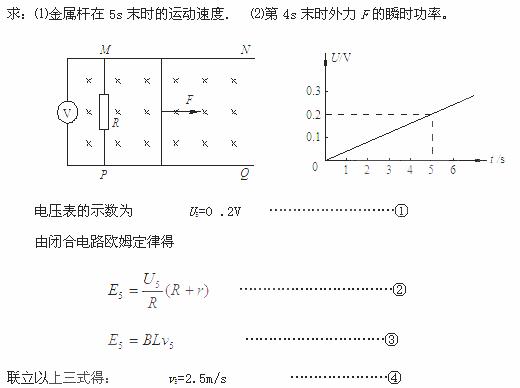
⑵由乙图可知,R两端电压随时间均匀变化,所以电路中的电流也随时间均匀变化,由闭合电路欧姆定律知,棒上产生的电动势也是随时间均匀变化的。因此由E=BLv可知,金属杆所做的运动为匀变速直线运动 ……………………………⑤
由⑴问中的④式有 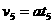
所以
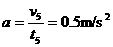 ……………………………⑥
……………………………⑥
所以4s末时的速度
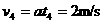 ……………………………⑦
……………………………⑦
所以4s末时电路中的电流为 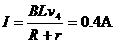 ……………………⑧
……………………⑧
因
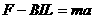
 ……………………⑨
……………………⑨
3、(1)在时刻t,棒的速度 v=a t
棒中感应电动势为 E=B L v=B L a t
棒中的感应电流为
I=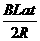 (4分)
(4分)
由牛顿第二定律 F-BIL=ma
得
F=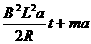 (4分)
(4分)
(2)细线拉断时满足
BIL=f +T0 (3分)
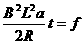 +T0
+T0
t=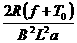 (4分)
(4分)
3.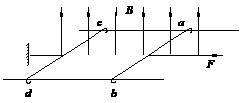 如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中,有两条足够长的平行金属导轨,其电阻不计,间距为L,导轨平面与磁场方向垂直。ab、cd为两根垂直导轨放置的、电阻都为R、质量都为m的金属棒。棒cd用能承受最大拉力为T0的水平细线拉住,棒cd与导轨间的最大静摩擦力为f 。棒ab与导轨间的摩擦不计,在水平拉力F的作用下以加速度a由静止开始向右做匀加速直线运动,求:
如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中,有两条足够长的平行金属导轨,其电阻不计,间距为L,导轨平面与磁场方向垂直。ab、cd为两根垂直导轨放置的、电阻都为R、质量都为m的金属棒。棒cd用能承受最大拉力为T0的水平细线拉住,棒cd与导轨间的最大静摩擦力为f 。棒ab与导轨间的摩擦不计,在水平拉力F的作用下以加速度a由静止开始向右做匀加速直线运动,求:
(1)线断以前水平拉力F随时间t的变化规律;
(2)经多长时间细线将被拉断。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com