
题目列表(包括答案和解析)
7.(2010·济南市三模)据中新社3月13日消息,我国将于2011年上半年发射“天宫一号”目标飞行器,“天宫一号”毁是交会对接目标飞行器,也是一个空间实验室,将以此为平台开展空间实验室的有关技术验证。假设“天宫一号”绕地球做半径为r,周期为T1的匀速圆周运动,地球绕太阳做半径为r2、周期为T2的匀速圆周运动,已知万有引力常量为G,则根据题中的条件可以求得 ( )
A.太阳的质量 B.“天宫一号”的质量
C.“天宫一号”与地球间万有引力 D.地球与太阳间的万有引力
6.如图4所示,在斜面顶端a处以速度va水平抛出一小球,经过时间ta恰好落在斜面底端P处;今在P点正上方与a等高的b处以速度vb
水平抛出另一小球,经过时间tb恰好落在斜面的中点处.若不计空气阻力,下列关系式正确的是( )

5. “嫦娥一号”月球探测器在环绕月球运行过程中,设探测器运行的轨道半径为r,运行速率为v,当探测器运行到月球上一些环形山中的质量密集区上空时( )
A.r、v都将略为减小
B.r、v都将保持不变
C.r将略为减小,v将略为增大
D.r将略为增大,v将略为减小
4、(2010·东北师大模拟)小河宽为d,河水中各点水流速度大小与各点到较近河岸边的距离成正比,v水= kx , k=4v0/d ,x是各点到近岸的距离,v0是小船划水速度。小船船头始终垂直河岸渡河,则下列说法中正确的是
A.小船的运动轨迹为直线
B.小船渡河所用的时间与水流速度大小无关
C.小船渡河时的实际速度是先变小后变大
D.小船到达离河对岸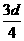 处,船的渡河速度为
处,船的渡河速度为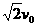
3. 由于地球的自转,在地球表面上,除了两极以外,任何物体都要随地球的自转而做匀速圆周运动,同一物体,当位于北京和上海两个不同地方的时候,可以判断(只考虑地球对物体的作用力)( )
A.该物体在北京和上海时所受的合力都指向地心
B.在北京时所受的重力大
C.在上海时随地球自转的线速度大
D.在上海时的向心加速度大
2. 如图2所示,螺旋形光滑轨道竖直放置, P、Q为对应的轨道最高点,一个小球以一定速度沿轨道切线方向进入轨道,且能过轨道最高点P,则下列说法中正确的是( )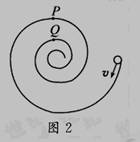
A.轨道对小球做正功,小球的线速度vP>vQ
B.轨道对小球不做功,小球的角速度ωP<ωQ
C.小球的向心加速度aP>aQ
D.轨道对小球的压力FP>FQ
1. 质点仅在恒力F的作用下,由O点运动到A点的轨迹如图1所示,在A点时速度的方向与x轴平行,则恒力F的方向可能沿( )
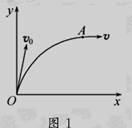
A.x轴正方向 B.x轴负方向
C.y轴正方向 D.y轴负方向
17.(11分)(2009·安徽省六校联考)如图所示,为某种新型设备内部电、磁场分布情况图.自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域.区域Ⅰ宽度为d1,分布有沿纸面向下的匀强电场E1;区域Ⅱ宽度为d2,分布有垂直纸面向里的匀强磁场B1;宽度可调的区域Ⅲ中分布有沿纸面向下的匀强电场E2和垂直纸面向里的匀强磁场B2.现在有一群质量和带电荷量均不同的带正电粒子从区域Ⅰ上边缘的注入孔A点被注入,从静止开始运动,然后相继进入Ⅱ、Ⅲ两个区域,满足一定条件的粒子将回到区域Ⅰ,其他粒子则从区域Ⅲ飞出.三区域都足够长,粒子的重力不计.
已知能飞回区域Ⅰ的带电粒子的质量为m=6.4×10-27kg,带电荷量为q=3.2×10-19C,且d1=10cm,d2=5cm,d3>10cm,E1=E2=40V/m,B1=4×10-3T,B2=2×10-3T.
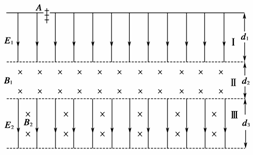
试求:
(1)该带电粒子离开区域Ⅰ时的速度.
(2)该带电粒子离开区域Ⅱ时的速度.
(3)该带电粒子第一次回到区域Ⅰ的上边缘时离开A点的距离.
[答案] (1)2×104m/s 方向竖直向下
(2)2×104m/s 方向与x轴正向成45°角
(3)57.26cm
[解析] (1)qE1d1=mv2
得:v=2×104m/s,方向竖直向下.
(2)速度大小仍为v=2×104m/s,如图所示.
qB1v=m
方向:sinθ=
可得:θ=45°
所以带电粒子离开区域Ⅱ时的速度方向与x轴正向成45°角.
(3)设该带电粒子离开区域Ⅱ也即进入区域Ⅲ时的速度分解为vx、vy,则:vx=vy=vsin45°=×104m/s
所以:qB2vx=qB2vy=1.28×10-17N.
qE2=1.28×10-17N
qE2=qB2vx
所以带电粒子在区域Ⅲ中运动可视为沿x轴正向的速率为vx的匀速直线运动和以速率为vy,以及对应洛伦兹力qB2vy作为向心力的匀速圆周运动的叠加,轨道如图所示:
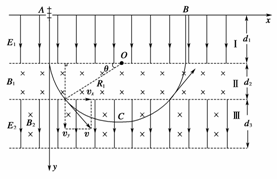
R2==10cm
T==π×10-5s
根据运动的对称性可知,带电粒子回到区域Ⅰ的上边缘的B点,距A点的距离为:d=2
代入数据可得:d≈57.26cm
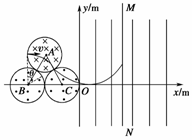
16.(11分)(2009·北京模拟)在坐标系xOy中,有三个靠在一起的等大的圆形区域,分别存在着方向如图所示的匀强磁场,磁感应强度大小都为B=0.10T,磁场区域半径r=m,三个圆心A、B、C构成一个等边三角形,B、C点都在x轴上,且y轴与圆形区域C相切,圆形区域A内磁场垂直纸面向里,圆形区域B、C内磁场垂直纸面向外.在直角坐标系的第Ⅰ、Ⅳ象限内分布着场强E=1.0×105N/C的竖直方向的匀强电场,现有质量m=3.2×10-26kg,带电荷量q=-1.6×10-19C的某种负离子,从圆形磁场区域A的左侧边缘以水平速度v=106m/s沿正对圆心A的方向垂直磁场射入,求:
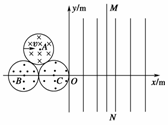
(1)该离子通过磁场区域所用的时间.
(2)离子离开磁场区域的出射点偏离最初入射方向的侧移为多大?(侧移指垂直初速度方向上移动的距离)
(3)若在匀强电场区域内竖直放置一挡板MN,欲使离子打到挡板MN上的偏离最初入射方向的侧移为零,则挡板MN应放在何处?匀强电场的方向如何?
[答案] (1)4.19×10-6s (2)2m
(3)MN应放在距y轴2m的位置上 竖直向下
[解析] (1)离子在磁场中做匀速圆周运动,在A、C两区域的运动轨迹是对称的,如图所示,设离子做圆周运动的半径为R,圆周运动的周期为T,由牛顿第二定律得:qvB=m
又T=
解得:R=,T=
将已知量代入得:R=2m
设θ为离子在区域A中的运动轨迹所对应圆心角的一半,由几何关系可知离子在区域A中运动轨迹的圆心恰好在B点,
则:tanθ==
θ=30°
则离子通过磁场区域所用的时间为:
t==4.19×10-6s
(2)由对称性可知:离了从原点O处水平射出磁场区域,由图可知侧移为
d=2rsin2θ=2m
(3)欲使离子打到挡板MN上时偏离最初入射方向的侧移为零,则离子在电场中运动时受到的电场力方向应向上,所以匀强电场的方向向下
离子在电场中做类平抛运动,加速度大小为:
a=Eq/m=5.0×1011m/s2
沿y方向的位移为:
y=at2=d
沿x方向的位移为:x=vt
解得:x=2m
所以MN应放在距y轴2m的位置.
15.(10分)如图所示,在竖直平面内有范围足够大、场强方向水平向左的匀强电场,在虚线的左侧有垂直纸面向里的匀强磁场,磁感应强度大小为B.一绝缘“⊂”形杆由两段直杆和一半径为R为半圆环组成,固定在纸面所在的竖直平面内.PQ、MN与水平面平行且足够长,半圆环MAP在磁场边界左侧,P、M点在磁场界线上,NMAP段是光滑的,现有一质量为m、带电量为+q的小环套在MN杆上,它所受到的电场力为重力的倍.现在M右侧D点由静止释放小环,小环刚好能到达P点,求:
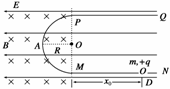
(1)D、M间的距离x0;
(2)上述过程中小环第一次通过与O等高的A点时弯杆对小环作用力的大小;
(3)若小环与PQ杆的动摩擦因数为μ(设最大静摩擦力与滑动摩擦力大小相等).现将小环移至M点右侧5R处由静止开始释放,求小环在整个运动过程中克服摩擦力所做的功.
[答案] (1)4R (2)mg+qB (3)mgR
[解析] (1)由动能定理得:qEx0-2mgR=0
qE=mg
∴x0=4R.
(2)设小环在A点速度为vA
由动能定理得:qE(x0+R)-mgR=mv
vA=
由向心力公式得:N-qvAB-qE=m
N=mg+qB.
(3)若μmg≥qE即μ≥,则小环运动到P点右侧s1处静止qE(5R-s1)-mg·2R-μmgs1=0
∴s1=
∴小环克服摩擦力所做的功W1=μmgs1=
若μmg<qE即μ<,则小环经过往复运动,最后只能在P、D之间运动,设小环克服摩擦力所做的功为W2,则qE5R-mg2R-W2=0
∴W2=mgR.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com