
题目列表(包括答案和解析)
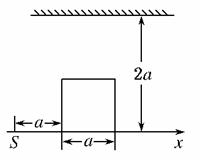
3.如图所示,在x轴的原点放一点光源S,距点光源为a处,放一不透光的边长为a的正方体物块,若在x轴的上方距x轴为2a处放一个平行于x轴并且面向物块的长平面镜,则在x轴上正方体的右边有部分区域被镜面反射来的光照亮,当点光源沿x轴向右移动的距离为多少时,正方体的右侧x轴上被光照亮部分将消失()
A.a
B.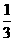 a
a
C. a
a
D.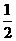 a
a
解析:如图所示,当S在2位置时光线部分刚好被挡住而消失,由几何关系可知2位置在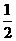 a处,所以选D.
a处,所以选D.

答案:D
2.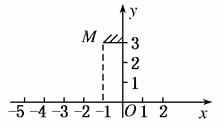 如图所示,在平面坐标轴xOy上,平面镜M两端的坐标分别为(-1,3)和(0,3),人眼位于坐标(2,0)处,当一发光点S从坐标原点沿-x方向运动过程中经以下哪个区域,人眼可以从平面镜中观察到S的图像?()
如图所示,在平面坐标轴xOy上,平面镜M两端的坐标分别为(-1,3)和(0,3),人眼位于坐标(2,0)处,当一发光点S从坐标原点沿-x方向运动过程中经以下哪个区域,人眼可以从平面镜中观察到S的图像?()
A.0到-1区域
B.-1到-2区域
C.0到-∞区域
D.-2到-4区域
解析:如图所示,由平面镜成像及相似三角形知识知D项正确.

 答案:D
答案:D
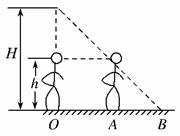
1.一人自街上路灯的正下方经过,看到自己头部的影子正好在自己脚下,如果人以不变的速度直线朝前走,则他自己头部的影子相对于地的运动情况是()
A.匀速直线运动
B.匀加速直线运动
C.变加速直线运动
 D.曲线运动
D.曲线运动
解析:设灯高为H、人高为h,如图人以速度v经任意时间t到达A,人头的影子在图示B处,由几何知识得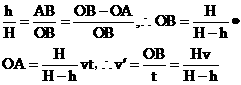 .v′为定值,即人头的影子做匀速直线运动.
.v′为定值,即人头的影子做匀速直线运动.
答案:A
5.如图所示,平面镜M以角速度ω=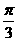 rad/s绕垂直于纸面且过O点的轴顺时针转动,AB为一段圆弧屏幕,它的圆心在O点,张角为60°,现有一束来自频闪光源的细平行光线以一个固定的方向射向平面镜M上的O点,光源每秒闪12次,则平面镜每转一周在屏幕AB上出现的亮点数最多可能是几个?
rad/s绕垂直于纸面且过O点的轴顺时针转动,AB为一段圆弧屏幕,它的圆心在O点,张角为60°,现有一束来自频闪光源的细平行光线以一个固定的方向射向平面镜M上的O点,光源每秒闪12次,则平面镜每转一周在屏幕AB上出现的亮点数最多可能是几个?
解析:由ω=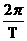 可得平面镜转动的周期T=6s,平面镜转过30°对应AB上的光点转过60°,所需时间为
可得平面镜转动的周期T=6s,平面镜转过30°对应AB上的光点转过60°,所需时间为 =0.5s,光源每秒闪12次,0.5s内将闪6次,若第一次光点正好照到B点,则屏幕上形成的最后一个光点恰好照到A点,这样在0.5s内实际上有7个光点出现在屏幕AB上.
=0.5s,光源每秒闪12次,0.5s内将闪6次,若第一次光点正好照到B点,则屏幕上形成的最后一个光点恰好照到A点,这样在0.5s内实际上有7个光点出现在屏幕AB上.
答案:7个
课时作业四十四光的直线传播光的反射
4.半径为R的圆柱体放在地面上,在距地面4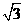 R的上方放一与地面平行的平面镜MN;在圆柱体左侧地面上有一点光源S,地面上圆柱体右侧AB部分没有被光线照到,如图所示.已知SB=8R,试求AB的长度.
R的上方放一与地面平行的平面镜MN;在圆柱体左侧地面上有一点光源S,地面上圆柱体右侧AB部分没有被光线照到,如图所示.已知SB=8R,试求AB的长度.
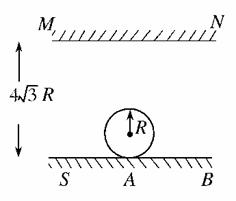
解析:光路图如下图所示,

由物像对称可知SS′=8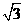 R,
R,
所以tanβ= ,所以β=60°则
,所以β=60°则
AB=R5cot =
=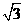 R
R
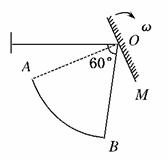 答案:
答案: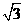 R
R
3.凌日是内行星经过日面的一种天文现象.我们把绕日运行轨道在地球以内的行星,称为内行星.如果内行星的一颗恰好从地球与太阳之间经过,地球上的观察者就会看到有一个黑点从太阳圆面通过,大约需要一个多小时,人们把这种现象称为凌日.根据上面的材料可知下面说法正确的是()

A.地球上的人们能看到的只有水星和金星凌日
B.发生凌日现象属于光的折射现象
C.发生凌日现象属于光的直线传播现象
D.凌日现象是人们看到的内行星的影子
答案:ACD
2. 一个点光源S,放在平面镜MN前.若MN不动,光源S以速率2m/s沿与镜面成60°角的方向向右做匀速直线运动,如图所示,则光源在镜中的像将( )
一个点光源S,放在平面镜MN前.若MN不动,光源S以速率2m/s沿与镜面成60°角的方向向右做匀速直线运动,如图所示,则光源在镜中的像将( )
A.以2m/s的速率做直线运动,且运动方向与S的运动方向夹角为120°
B.以2m/s的速率垂直于MN做直线运动
C.以 槡2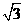 m/s的速率相对于S做直线运动
D.以 槡2
m/s的速率相对于S做直线运动
D.以 槡2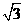 m/s的垂直于MN的速率向MN做直线运动
m/s的垂直于MN的速率向MN做直线运动
解析:根据平面镜成像规律,作S的像S′,如右图所示,经过t时间,光源S的位置为S1,其像就为S′1.由物像对称性可知SS1=S′S′1,所以S′相对平面镜是以2m/s的速率,沿与镜成60°角的S′O方向做匀速直线运动,并且与S的运动方向SO的夹角为120°,所以选项A是正确的,B是错误的.S的速度为v,垂直于平面镜的分速度 1=
1= 5cos30°=2×
5cos30°=2× m/s,由物像对称性知,S′相对于镜的垂直分速度也为
m/s,由物像对称性知,S′相对于镜的垂直分速度也为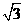 m/s,所以选项D是错误的.若以S为参照物,则S′相对于S是以2
m/s,所以选项D是错误的.若以S为参照物,则S′相对于S是以2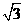 m/s的速率向S做匀速直线运动,所以选项C是正确的.
m/s的速率向S做匀速直线运动,所以选项C是正确的.
答案:AC
1.如图所示,为发生日食时影区的分布情况,则下列叙述中正确的是()
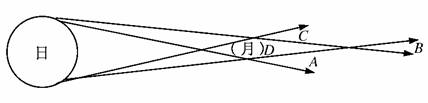
A.在D区的观察者可观察到日环食
B.在B区的观察者可观察到日全食
C.在A区的观察者可观察到日全食
D.在A区的观察者可观察到日偏食
解析:由题图所示的光路及本影,半影的定义可知: D是本影区,A,C为半影区,B是本影D的倒圆锥体,进入B区的光线均为太阳周围的光线,故有A,C区观察均为日偏食,在B区观察为日环食.所以,D选项正确.
答案:D
12.如图所示,玻璃棱镜ABCD可以看成是由ADE、ABE、BCD三个直角三棱镜组成.一束频率为5.3×1014Hz的单色细光束从AD面入射,在棱镜中的折射光线如图中ab所示,ab与AD面的夹角α=60°.已知光在真空中的速度c=3×108m/s,玻璃的折射率n=1.5,求:

(1)这束入射光线的入射角多大?
(2)该束光线第一次从CD面出射时的折射角.(结果可用三角函数表示)
解析:(1)设光在AD面的入射角、折射角分别为i、r,r=30°,根据n=
得sini=nsinr=1.5×sin30°=0.75,i=arcsin0.75.
(2)光路如图所示,ab光线在AB面的入射角为45°,设玻璃的临界角为C,则sinC=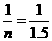 =0.67
=0.67

sin45°>0.67,因此光线ab在AB面会发生全反射,光线在CD面的入射角r′=r=30°
根据n=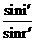 ,光线从CD面的出射光线与法线的夹角i′=i=arcsin0.75.
,光线从CD面的出射光线与法线的夹角i′=i=arcsin0.75.
答案:(1)arcsin0.75 (2)arcsin0.75
11.如图所示,一个半径为r的圆木板静止在水面上,在圆木板圆心O的正下方H=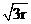 处有一点光源S,已知水的折射率n=
处有一点光源S,已知水的折射率n=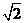 .
.
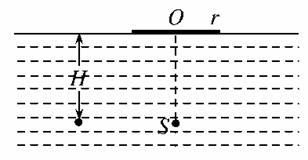
(1)求沿圆木板边缘出射的折射光线的折射角.
(2)若要在水面上方观察不到点光源S所发出的光,则应将点光源S至少竖直向上移多大的距离?(结果可用根式表示)
解析:(1)设入射角为θ1,折射角为θ2,则tanθ1=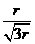 ①
①
即θ1=30°②
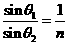 ③
③
联立①②③式得θ2=45°.④
(2)若在水面上方观察不到点光源所发出的光,则入射到圆木板边缘的光线将发生全反射,设临界角为C,点光源S离圆心的距离为h,则由sinC=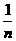 得⑤
得⑤
C=45°⑥
由几何关系tanC= 得⑦
得⑦
h=r⑧
则点光源S至少上移Δh=(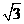 -1)r.⑨
-1)r.⑨
答案:(1)45° (2)(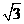 -1)r
-1)r
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com