6．据报道，“嫦娥一号”和“嫦娥二号”绕月飞行器的圆形工作轨道距月球表面分别约为200km和100km，运行速率分别为v₁和v₂.那么，v₁和v₂的比值为(月球半径取1700km)　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　　B.　　C.　　D.

[解析]　本题考查天体运动中卫星的速度问题，意在考查考生对天体运动的认识和匀速圆周运动的基本知识．根据卫星运动的向心力由万有引力提供，有G＝m，那么卫星的线速度跟其轨道半径的平方根成反比，则有＝＝.

[答案]　C

5．天文学家新发现了太阳系外的一颗行星．这颗行星的体积是地球的4.7倍，质量是地球的25倍．已知某一近地卫星绕地球运动的周期约为1.4小时，引力常量G＝6.67×10^－11N·m²/kg²，由此估算该行星的平 均密度约为　　　　　　　 　　 (　)

A．1.8×10³kg/m³　　　　　　　 B．5.6×10³kg/m³

C．1.1×10⁴kg/m³　 　　　　　　　　　 D．2.9×10⁴kg/m³

[解析]　本题考查万有引力定律在天文学上的应用和人造地球卫星问题，意在考查考生对天体运动问题的处理能力．近地卫星绕地球做圆周运动时，所受万有引力充当其做圆周运动的向心力，即：G＝m()²R，由密度、质量和体积关系M＝ρ·πR³解两式得：ρ＝≈5.60×10³kg/m³.由已知条件可知该行星密度是地球密度的25/4.7倍，即ρ＝5.60×10³×kg/m³＝2.9×10⁴kg/m³，D正确．

[答案]　D

4．发射人造卫星是将卫星以一定的速度送入预定轨道．发射场一般选择在尽可能靠近赤道的地方，如图所示．这样选址的优点是，在赤道附近　　　 　 (　)

A．地球的引力较大

B．地球自转线速度较大

C．重力加速度较大

D．地球自转角速度较大

[解析]　本题考查圆周运动和万有引力定律，意在考查考生将所学的知识应用到实际问题中的能力．地球的自转角速度是一定的，根据线速度与角速度的关系v＝rω可知，离赤道近的地方地球表面的线速度较大，所以发射人造地球卫星较容易，故正确答案为B.

[答案]　B

3．2月11日，俄罗斯的“宇宙－2251”卫星和美国的“铱－33”卫星在西伯利亚上空约805km处发生碰撞．这是历史上首次发生的完整在轨卫星碰撞事件．碰撞过程中产生的大量碎片可能会影响太空环境．假定有甲、乙两块碎片，绕地球运动的轨道都是圆，甲的运行速率比乙的大，则下列说法中正确的是　　　　　　 (　)

A．甲的运行周期一定比乙的长

B．甲距地面的高度一定比乙的高

C．甲的向心力一定比乙的小

D．甲的加速度一定比乙的大

[解析]　本题考查的是万有引力与航天的有关知识，意在考查考生对绕地卫星的线速度与半径、周期、向心力等之间关系的理解和应用能力；根据公式T＝2π可知：A错误；再根据公式v＝可知：B错误；由于甲离地球较近，故向心力较大，所以C错误，D正确．

[答案]　D

2．关于地球的第一宇宙速度，下列表述正确的是　　　　 (　)

A．第一宇宙速度又叫环绕速度

B．第一宇宙速度又叫脱离速度

C．第一宇宙速度跟地球的质量无关

D．第一宇宙速度跟地球的半径无关

[答案]　A

1．在讨论地球潮汐成因时，地球绕太阳运行轨道与月球绕地球运行轨道可视为圆轨道．已知太阳质量约为月球质量的2.7×10⁷倍，地球绕太阳运行的轨道半径约为月球绕地球运行的轨道半径的400倍．关于太阳和月球对地球上相同质量海水的引力，以下说法正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．太阳引力远大于月球引力

B．太阳引力与月球引力相差不大

C．月球对不同区域海水的吸引力大小相等

D．月球对不同区域海水的吸引力大小有差异

16.(12分)一辆实验小车可沿水平地面(图中纸面)上的长直轨道匀速向右运动.有一台发出细光束的激光器装在小转台M上，到轨道的距离MN为d=10 m，如图14-10所示，转台匀速转动，使激光束在水平面内扫描，扫描一周的时间为T=60 s，光束转动方向如图中箭头所示，当光束与MN的夹角为45°时，光束正好射到小车上，如果再经过Δt=2.5 s光束又射到小车上，则小车的速度为多少？(结果保留两位有效数字)

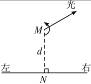
图14-10

解析:本题考查光的直线传播和匀速圆周运动规律，是一道设计新颖的好题，要求学生画出小车运动位置的示意图，才能求出符合题意的两个结果.在Δt内光束转过角度为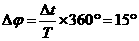(①式)，如图所示，有两种可能:

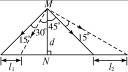
(1)光束照射小车时，小车正在接近N点，Δt内光束与MN的夹角从45°变为30°，小车走过l₁，速度应为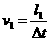(②式)；由图可知

l₁=d(tan45°－tan30°)(③式)

由②③两式并代入数值，得v₁=1.7 m/s(④式).

(2)光束照射小车时，小车正在远离N点，Δt内光束与MN的夹角从45°变为60°，小车走过l₂，速度应为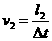(⑤式)

由图可知l₂=d(tan60°－tan45°)(⑥式)

由⑤⑥两式并代入数值，得v₂=2.9 m/s.

答案:(1)当光束照射小车时，小车正在接近N点，这时小车的速度应为1.7 m/s；(2)当光束照射小车时，小车正远离N点，这时小车的速度应为2.9 m/s.

15.(10分)用金属钠作阴极的光电管，如图14-9所示连入电路，已知能使电路中有光电流的最大波长为540 nm，若用波长为4.34×10^{－7 m}的紫外线照射阴极，求:

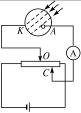
图14-9

(1)阴极所释放光电子的最大初速度为多少？

(2)将滑片C向左移动，使K的电势高于A的电势时，电流表中还有无光电流？当O、C间的电压U₁为多大时，电流表中的电流为零？

解析:(1)逸出功W＝hc/λ₀＝3.68×10^－19 J

最大初动能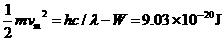

则光电子最大初速度

v_m＝4.46×10⁵ m/s.

(2)当K极板电势高于A极时，还可能有光电流，因为K极板逸出的光电子尚有初动能，可克服电场力做功到达A板，从而形成光电流.但电压升高到U₁，使得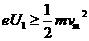时，就不能形成光电流了，即

答案:(1)4.4 6×10⁵ m/s

(2)可能有，也可能没有　0.56 V

14.(10分)为从军事工事内部观察外面的目标,在工事壁上开一长方形孔,设工事壁厚d=34.64 cm,孔的宽度L=20 cm,孔内嵌入折射率n=3的玻璃砖,如图148所示.试问:

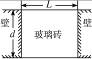
图14-8

(1)嵌入玻璃砖后,工事内部人员观察到外界的视野的最大张角为多少?

(2)要想使外界180°范围内的景物全被观察到,则应嵌入折射率多大的玻璃砖?

解析:工事内部的人从内壁左侧能最大范围观察右边的目标.光路如图所示.

已知d=34.64 cm,L=20 cm,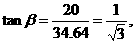,所以β=30°.

(1)由折射定律有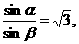得α=60°

即视野的张角最大为120°.

(2)要使视野的张角为180°,即α′=90°

由折射定律有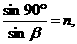所以n=2.

答案:(1)120°　(2)2

13.(10分)如图14-7所示，置于空气中的一个不透明容器内盛满某种透明液体.容器底部靠近器壁处有一竖直放置的6.0 cm长的线光源.靠近线光源一侧的液面上盖有一遮光板，另一侧有一水平放置的与液面等高的望远镜，用来观察线光源.开始时通过望远镜不能看到线光源的任何一部分.将线光源沿容器底向望远镜一侧平移至某处时，通过望远镜刚好可以看到线光源底端，再将线光源沿同一方向移动8.0 cm，刚好可以看到其顶端.求此液体的折射率n.

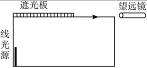
图14-7

解析:若线光源底端在A点时，望远镜内刚好可看到线光源的底端，则有:∠AOO′=α

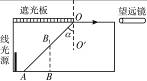
其中α为此液体到空气的全反射临界角，由折射定律得: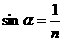

同理，线光源顶端在B₁点时，望远镜内刚好可看到线光源的顶端，则:∠B₁OO′=α

由图中几何关系得: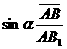

解得: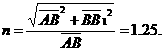

答案:1.25