3．在氢原子光谱中，电子从较高能级跃迁到n＝2能级发出的谱线属于巴耳末线系．若一群氢原子自发跃迁时发出的谱线中只有2条属于巴耳末线系，则这群氢原子自发跃迁时最多可发出________条不同频率的谱线．

[答案]　6

[解析]　因该群氢原子自发跃迁时发出的谱线中只有2条属于巴耳末线系，故该群氢原子处于n＝4激发态，故由n＝4激发态自发跃迁时最多可发出6条不同频率的谱线．

2．一个盒子放在小车上，小车在光滑的水平面上运动，雨水沿竖直方向以0.1kg/(m²·s)的下落速率落进盒子，起始小车和盒子的质量为5kg，速度2m/s.若盒子的面积为0.5m²，则100s后小车运动的速率为________m/s.

[答案]　1

[解析]　落入盒子中的水和小车系统水平方向不受外力，系统水平方向动量守恒

m_水＝100×0.5×0.1kg＝5kg

m_车v₀＝(m_车+m_水)v，v＝＝1m/s.

1．某考古队发现一古生物骸骨．考古专家根据骸骨中C的含量推断出了该生物死亡的年代．已知此骸骨中C的含量为活着的生物体中C的1/4，C的半衰期为5730年．该生物死亡时距今约________年．

[答案]　1.1×10⁴(11460或1.0×10⁴-1.2×10⁴都正确)

[解析]　由题意知，所求时间为C的两个半衰期．

即t＝2×5730＝11460(年)．

13．天文学家们通过观测的数据确认了银河系中央的黑洞“人马座A^*”的质量与太阳质量的倍数关系．研究发现，有一星体S2绕人马座A^*做椭圆运动，其轨道半长轴为9.50×10²天文单位(地球公转轨道的半径为一个天文单位)，人马座A^*就处在该椭圆的一个焦点上．观测得到S2星的运行周期为15.2年．

(1)若将S2星的运行轨道视为半径r＝9.50×10²天文单位的圆轨道，试估算人马座A^*的质量M_A是太阳质量M_S的多少倍(结果保留一位有效数字)；

(2)黑洞的第二宇宙速度极大，处于黑洞表面的粒子即使以光速运动，其具有的动能也不足以克服黑洞对它的引力束缚．由于引力的作用，黑洞表面处质量为m的粒子具有的势能为E_p＝－G(设粒子在离黑洞无限远处的势能为零)，式中M、R分别表示黑洞的质量和半径．已知引力常量G＝6.7×10^－11N·m²/kg²，光速c＝3.0×10⁸m/s，太阳质量M_S＝2.0×10³⁰kg，太阳半径R_S＝7.0×10⁸m，不考虑相对论效应，利用上问结果，在经典力学范围内求人马座A^*的半径R_A与太阳半径R_S之比应小于多少(结果按四舍五入保留整数．)

[解析]　(1)S2星绕人马座A^*做圆周运动的向心力由人马座A^*对S2星的万有引力提供，设S2星的质量为m_S2，角速度为ω，周期为T，则

G＝m_S2ω²r　①

ω＝　②

设地球质量为m_E，公转轨道半径为r_E，周期为T_E，则

G＝m_E()²r_E　③

综合上述三式得＝()³()²

式中T_E＝1年　④

r_E＝1天文单位　⑤

代入数据可得＝4×10⁶　⑥

(2)引力对粒子作用不到的地方即为无限远，此时粒子的势能为零．“处于黑洞表面的粒子即使以光速运动，其具有的动能也不足以克服黑洞对它的引力克缚”，说明了黑洞表面处以光速运动的粒子在远离黑洞的过程中克服引力做功，粒子在到达无限远之前，其动能便减小为零，此时势能仍为负值，则其能量总和小于零．根据能量守恒定律，粒子在黑洞表面处的能量也小于零，则有

mc²－G<0　⑦

依题意可知R＝R_A，M＝M_A

可得R_A<　⑧

代入数据得R_A<1.2×10¹⁰m　⑨

<17　⑩

12． 3月1日，完成使命的“嫦娥一号”卫星成功撞击月球．“嫦娥一号”卫星在北京航天飞行控制中心科技人员的精确控制下，15时36分，卫星启动发动机开始变轨，然后关闭发动机沿抛物线下落，16时13分10秒成功落在月球的丰富海区域．撞击产生了高达10km的尘埃层，设尘埃在空中时只受到月球的引力．模拟撞击实验显示，尘埃能获得的速度可达到撞击前卫星速度的11%；在卫星变轨过程中，航天飞行控制中心还测得，卫星在离月球表面高176km的圆轨道上运行的周期为T₁＝125min，在近月(高度不计)圆轨道上运行的周期T₂＝107.8min.计算时取＝4.76.试估算(结果保留两位有效数字)：

(1)月球半径R和月球表面重力加速度g；

(2)空中尘埃层存在的时间．

[解析]　(1)由万有引力定律得G＝＝m(R+h)　①

G＝mR　②

由①、②得＝

R＝·h≈1.7×10⁶m　③

g＝R＝1.6m/s²　④

(2)上升最高的尘埃做竖直上抛运动，因此由H＝gt得

t＝2t_下＝2＝2.2×10²s

11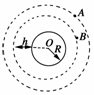．如图所示，A是地球的同步卫星．另一卫星B的圆形轨道位于赤道平面内，离地面高度为h.已知地球半径为R，地球自转角速度为ω₀，地球表面的重力加速度为g，O为地球中心．

(1)求卫星B的运行周期．

(2)如果卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、B、A在同一直线上)，则至少经过多长时间，它们再一次相距最近？

[解析]　(1)由万有引力定律和向心力公式得

G＝m(R+h)①

G＝mg②

联立①②解得：

T_B＝2π③

(2)由题意得：(ω_B－ω₀)t＝2π④

由③得：ω_B＝⑤

将⑤代入④得：t＝.

[答案]　(1)2π　(2)

10．我国在今、明两年将发射10颗左右的导航卫星，预计在2015年建成由30多颗卫星组成的“北斗二号”卫星导航定位系统，此系统由中轨道、高轨道和同步轨道卫星等组成．现在正在服役的“北斗一号”卫星定位系统的三颗卫星都定位在距地面36000km的地球同步轨道上．而美国的全球卫星定位系统(简称GPS)由24颗卫星组成，这些卫星距地面的高度均为20000km.则下列说法中正确的是　　　　　　　　 (　)

A．“北斗一号”系统中的三颗卫星的质量必须相等

B．GPS的卫星比“北斗一号”系统中的卫星周期短

C．“北斗二号”中的每颗卫星一定比“北斗一号”中的每颗卫星的加速度大

D．“北斗二号”中的中轨道卫星的线速度大于高轨道卫星的线速度

[解析]　“北斗一号”卫星系统中的三颗卫星的质量可以不相等，选项A错误；GPS的卫星距地面的高度小于“北斗一号”中的卫星，轨道半径较小，GPS的卫星比“北斗一号”的卫星周期短，选项B正确；卫星的加速度大小与卫星距地面高度有关，距地面越高，加速度越小，“北斗二号”卫星导航定位系统的卫星距地面高度不同，因此“北斗二号”中的每颗卫星的加速度不一定比“北斗一号”中的每颗卫星的加速度大，选项C错误；由Gmm′/r²＝m′v²/r得v＝，“北斗二号”中的中轨道卫星的轨道半径r小于高轨道卫星的轨道半径，所以“北斗二号”中的轨道卫星的线速度大于高轨道卫星的线速度，选项D正确．

[答案]　BD

9．近地人造卫星1和2绕地球做匀速圆周运动的周期分别为T₁和T₂.设在卫星1、卫星2各自所在的高度上的重力加速度大小分别为g₁、g₂，则　　　 (　)

A.＝()^4/3　 　　　　　　　　　 B.＝()^4/3

C.＝()²　 　　　　　　　　　　 D.＝()²

[解析]　本题考查万有引力和人造卫星，意在考查考生对人造卫星相关的物理量之间关系的理解和应用；因为近地卫星绕地球做匀速圆周运动，万有引力全部用来提供向心力，即有G＝mr，可得r＝，又可认为万有引力与重力相等，故有G＝mg，所以mg＝mr，由此可得：g＝r，将r＝代入得：g＝·＝＝，即g∝，所以＝()，B正确．

[答案]　B

8．英国《新科学家(New Scientist)》杂志评选出了年度世界8项科学之最，在XTEJ1650－500双星系统中发现的最小黑洞位列其中．若某黑洞的半径R约为45km，质量M和半径R的关系满足＝(其中c为光速，G为引力常量)，则该黑洞表面重力加速度的数量级为　　　　　　　　 　　　　　　　　　　　　　　　　 (　)

A．10⁸m/s²　 　　　　　　　　　　 B．10¹⁰m/s²

C．10¹²m/s²　 　　　　　　　　 D．10¹⁴m/s²

[解析]　本题考查的知识点为万有引力与天体运动，在能力的考查上突出考查了万有引力、天体与新发现的结合，属于信息题，在解题时要认真审题，读懂题意，此类试题是高考的热点．星球表面的物体满足mg＝G，即GM＝R²g，由题中所给条件＝推出GM＝Rc²，则GM＝R²g＝Rc²，代入数据解得g＝10¹²m/s²，C正确．

[答案]　C

7． 9月25日至28日，我国成功实施了“神舟七号”载人航天飞行并实现了航天员首次出舱．飞船先沿椭圆轨道飞行，后在远地点343千米处点火加速，由椭圆轨道变成高度为343千米的圆轨道，在此圆轨道上飞船运行周期约为90分钟．下列判断正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．飞船变轨前后的机械能相等

B．飞船在圆轨道上时航天员出舱前后都处于失重状态

C．飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度

D．飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度