1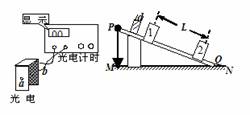．像打点计时器一样，光电计时器也是一种研究物体运动情况的常用计时仪器，其结构如图所示，a、b分别是光电门的激光发射和接收装置，当有物体从a、b间通过时，光电计时器就可以显示物体的挡光时间。现利用图9所示装置测量滑块和长lm左右的木块间的动摩擦因数，图中MN是水平桌面，Q是木板与桌面的接触点，1和2是固定在木板上适当位置的两个光电门，与之连接的两个光电计时器没有画出。此外在木板顶端的P点还悬挂着一个铅锤，让滑块从木板的顶端滑下，光电门l、2各自连接的计时器显示的挡光时间分别为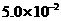s和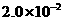s。用游标卡尺测量小滑块的宽度d=5.0cm.。

　 2．在学了自由落体运动这一部分内容后，有同学计算，若有雨滴从距地面2.5km高空自由落下，到达地面时速度将超过200m／s，事实上谁也未见过如此高速的雨滴．这引发了一些同学的思考：雨滴在下落时肯定受到了空气阻力的作用．那它究竟是如何运动的呢?有一组同学设计了一个实验，用胶木球在水中的自由下落来模拟雨滴在空气中的下落过程．实验中，胶木球从某一高度竖直落下，用闪光照相方法拍摄了小球在不同时刻的位置，如图所示．

(1)请你根据此闪光照片定性描述出小球的运动情形： _______________；

(2)对于小球下落时所受的阻力，我们可以作最简单的猜想：阻力(F)与小球速度(v)_________________，即F＝k__________( k为阻力常数)．已知照相机的闪光频率为f，图中刻度尺的最小分度为s₀，小球的质量为m．若猜想成立，则由此闪光照片及上述已知条件可求得胶木球在水中下落时的阻力常数k＝________________。

8．(2011·南京模拟)17世纪英国物理学家胡克发现：在弹性限度内，弹簧的形变量与弹力成正比，这就是著名的胡克定律．受此启发，一学习小组同学研究“金属线材伸长量与拉力的关系”的探究过程如下：

A．有同学认为：横截面为圆形的金属丝或金属杆在弹性限度内，其伸长量与拉力成正比，与截面半径成反比．

B．他们准备选用一些“由同种材料制成的不同长度、不同半径的线材”作为研究对象，用测距仪、传感器等仪器测量线材的伸长量随拉力变化的规律，以验证假设．

C．通过实验取得如下数据：

长度	拉力 　　　　 伸长 直径	250 N	500 N	750 N	1 000 N
1 m	2.52 mm	0.4 mm	0.8 mm	1.2 mm	1.6 mm
2 m	2.52 mm	0.8 mm	1.6 mm	2.4 mm	3.2 mm
1 m	3.57 mm	0.2 mm	0.4 mm	0.6 mm	0.8 mm

D．同学们对实验数据进行分析、归纳后，对他们的假设进行了补充完善．

(1)上述科学探究活动中，属于“制定计划”和“搜集证据”的环节分别是________、________.

7．橡皮筋也像弹簧一样，在弹性限度内，伸长量x与弹力F成正比，即F＝kx，k的值与橡皮筋未受到拉力时的长度L、横截面积S有关，理论与实践都表明k＝Y ，其中Y是一个由材料决定的常数，材料力学上称之为杨氏模量．

(1)在国际单位制中，杨氏模量Y的单位应该是　　　　　　　　　　　　　　 (　)

A．N　　　　　　 　B．m　　　　　　　　 C．N/m　　　　　 　D．Pa

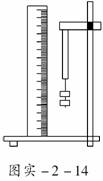
　(2)有一段横截面是圆形的橡皮筋，应用如图实－2－14所示的实验装置可　

以测量出它的杨氏模量Y的值．首先利用测量工具a测得橡皮筋的长度L　

＝20.00 cm，利用测量工具b测得橡皮筋未受到拉力时的直径D＝4.000 　

mm，那么测量工具a应该是____________，测量工具b应该是

__________．

(3)下面的表格是橡皮筋受到的拉力F与伸长量x的实验记录.

请作出F－x图象，由图象可求得该橡皮筋的劲度系数k＝________N/m.

(4)这种橡皮筋的Y值等于________．

解析：(1)在弹性限度内，弹力F与伸长量x成正比，F＝kx，又根据题意可知，k＝YS/L.

则F＝kx＝Y ·x

得出杨氏模量Y＝

各物理量取国际单位得杨氏模量的单位是N/m²＝Pa，选项D正确．

(2)根据精确度判断可知a为毫米刻度尺，b为螺旋测微器．

(3)根据表格数据，描点、连线，可得F－x图象如图所示．根据斜率的物量意义表示劲度系数k，

k＝≈3. 1×10² N/m.

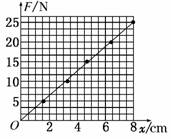
(4)根据Y＝kL/S求得，Y≈5×10⁶ Pa.

答案：(1)D　(2)毫米刻度尺　螺旋测微器　(3)图象见解析图　3.1×10²　(4)5×10⁶ Pa

6．某同学和你一起探究弹力和弹簧伸长的关系，并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上，然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧，并使弹簧另一端的指针恰好落在刻度尺上．当弹簧自然下垂时，指针指示的刻度数值记作L₀；弹簧下端挂一个50 g的砝码时，指针指示的刻度数值记作L₁；弹簧下端挂两个50 g的砝码时，指针指示的刻度数值记作L₂；……；挂七个50 g的砝码时，指针指示的刻度数值记作L₇.

(1)下表记录的是该同学已测出的6个值，其中有两个数值在记录时有误，它们的代表符号分别是________________和______________.

(2)实验中，L₃和L₇两个值还没有测定，请你根据图实－2－13将这两个测量值填入上表中．

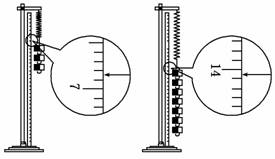
图实－2－13

(3)为了充分利用测量数据，该同学将所测得的数值按如下方法逐一求差，分别计算出了三个差值：d₁＝L₄－L₀＝6.90 cm，d₂＝L₅－L₁＝6.90 cm，d₃＝L₆－L₂＝7.00 cm.

请你给出第四个差值：d₄＝________＝________cm.

(4)根据以上差值，可以求出每增加50 g砝码的弹簧平均伸长量ΔL.ΔL用d₁、d₂、d₃、d₄表示的式子为：ΔL＝__________________________________________________，

代入数据解得ΔL＝________cm.

(5)计算弹簧的劲度系数k＝______________N/m.(g取9.8 m/s²)

解析：(1)L₅、L₆两组数据在读数时均没有估读值．

(2)根据表格已知读数，刻度尺上端的刻度数小，因而L₃＝6.85 cm，L₇＝14.05 cm.

(3)题中三组数据在寻求多挂4个砝码形成的长度差，故d₄＝L₇－L₃＝(14.05－6.85)cm＝7.20 cm.

(4)每增加4个砝码弹簧的平均伸长量ΔL₁＝，则每增加1个砝码弹簧的平均伸长量ΔL＝＝，代入数据求得ΔL＝1.75 cm.

(5)由(3)(4)可知，弹力F和弹簧伸长量ΔL成正比，即满足F＝kΔL，代入数据

k＝＝ N/m＝28 N/m.

答案：(1)L₅　L₆　(2)6.85　14.05

(3)L₇－L₃　7.20

(4)　1.75　(5)28

5．某同学用如图实－2－11所示装置做“探究弹力和弹簧伸长关系” 实验．他先测出不挂钩码时弹簧下端指针所指的标尺刻度，然后在弹簧下端挂上钩码，并逐个增加钩码，测出指针所指的标尺刻度，所得数据列表如下：(g取9.8 m/s²)

(1)根据所测数据，在图实－2－12所示的坐标纸上作出弹簧指针所指的标尺的刻度x与钩码质量m的关系曲线．

图实－2－12

(2)根据所测得的数据和关系曲线可以判断，在________N范围内弹力大小与弹簧伸长关系满足胡克定律，这种规格的弹簧的劲度系数为________N/m.

解析：(1)根据题目中所测量的数据进行描点，然后用平滑的曲线(或直线)连接各点，在连接时应让尽量多的点落在线上，偏差比较大的点舍去，不在线上的点尽量均匀分布在线的两侧，如图所示．

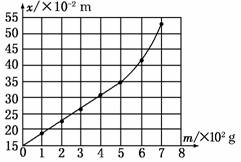
(2)根据所画图象可以看出，当m≤5.00×10² g＝0.5 kg时，标尺刻度x与钩码质量m成一次函数关系，所以在F≤4.9 N范围内弹力大小与弹簧伸长关系满足胡克定律，由胡克定律F＝kΔx可知，图线斜率的大小在数值上等于弹簧的劲度系数k，即

k＝＝＝25.0 N/m.

答案：(1)见解析　(2)0-4.9　25.0

4．用如图实－2－10甲所示的装置测定弹簧的劲度系数，被测弹簧一端固定于A点，另一端B用细绳绕过定滑轮挂钩码，旁边竖直固定一最小刻度为mm的刻度尺，当挂两个钩码时，绳上一定点P对应刻度如图实－2－10乙中ab虚线所示，再增加一个钩码后，P点对应刻度如图实－2－10乙中cd虚线所示，已知每个钩码质量为50 g，重力加速度g＝9.8 m/s²，则被测弹簧的劲度系数为________N/m.挂三个钩码时弹簧的形变量为________cm.

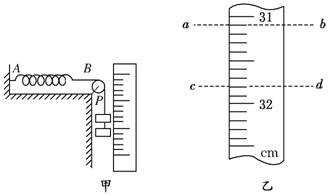
图实－2－10

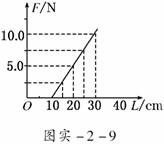
3．某同学在做“探究弹力和弹簧伸长的关系”的实验时，将一轻弹簧竖直悬挂并让其自然下垂，测出其自然长度；然后在其下部施加外力F，测出弹簧的总长度L，改变外力F的大小，测出几组数据，作出外力F与弹簧总长度L的关系图线如图实－2－9所示．(实验过程是在弹簧的弹性限度内进行的)

由图可知该弹簧的自然长度为________cm；该弹簧的劲度系数为________N/m.

解析：当外力F＝0时，弹簧的长度即原长L₀＝10 cm，图线的斜率就是弹簧的劲度系数，即k＝×10² N/m＝50 N/m.

答案：10　50

2．(2011·临沂质检)如图实－2－8甲所示，一个弹簧一端固定在传感器上，传感器与电脑相连．当对弹簧施加变化的作用力(拉力或压力)时，在电脑上得到了弹簧形变量与弹簧产生的弹力的关系图象，如图实－2－8乙所示．则下列判断正确的是　　 (　)

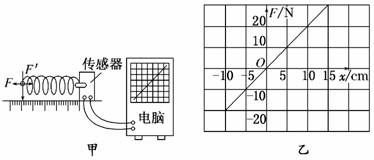
图实－2－8

A．弹簧产生的弹力和弹簧的长度成正比

B．弹力增加量与对应的弹簧长度的增加量成正比

C．该弹簧的劲度系数是200 N/m

D．该弹簧受到反向压力时，劲度系数不变

解析：由图乙知，F－x是一个过原点的直线，k＝ N/m＝200 N/m，可知A错，B、C、D正确．

答案：BCD

1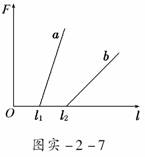．　 一个实验小组在“探究弹力和弹簧伸长的关系”的实验中，使用两条不同的轻质弹簧a和b，得到弹力与弹簧长度关系的图象如图实－2－7所示．

下列表述正确的是　 (　)

A．a的原长比b的长

B．a的劲度系数比b的大

C．a的劲度系数比b的小

D．测得的弹力与弹簧的长度成正比

解析：图象的横轴截距表示弹簧的原长，A错误；图象的斜率表示弹簧的劲度系数，B正确，C错误；图象不过原点，D错误．

答案：B

8．(2011·佛山联考)某研究性学习小组欲探究光滑斜面上物体下滑的加速度与物体质量及斜面倾角是否有关系．实验室提供如下器材：

A．表面光滑的长木板(长度为L)；B.小车；C.质量为m的钩码若干个；D.方木块(备用于垫木板)；E.米尺；F.秒表．

(1)实验过程：

第一步，在保持斜面倾角不变时，探究加速度与质量的关系．实验中，通过向小车放入钩码来改变物体的质量，只要测出小车由斜面顶端滑至底端所用的时间t，就可以由公式a＝________求出a，某同学记录了数据如下表所示：

质量 时间 t次数	M	M+m	M+2m
1	1.42	1.41	1.42
2	1.40	1.42	1.39
3	1.41	1.38	1.42

根据以上信息，我们发现，在实验误差范围内质量改变之后平均下滑时间________(填“改变”或“不改变”)，经过分析得出加速度和质量的关系为________．

第二步，在物体质量不变时，探究加速度与倾角的关系．实验中通过改变方木块垫放位置来调整长木板倾角，由于没有量角器，因此通过测量出木板顶端到水平面高度h，求出倾角α的正弦值sinα＝.某同学记录了高度h和加速度a的对应值如下表：

请先在如图实－4－15所示的坐标纸上建立适当的坐标轴后描点作图，然后根据所作的图线求出当地的重力加速度g＝________.进一步分析可知，光滑斜面上物体下滑的加速度与倾角的关系为______________________________________．

图实－4－15

(2)该探究小组所采用的探究方法是________________________________________．

解析：(1)由L＝at²得：a＝.

由表中可看出：在实验误差允许的范围内，小车下滑的时间是不变的，说明小车的加速度与小车的质量无关．

以a为纵轴，以sinα为横轴，选取适当的标度作出图象如图所示．

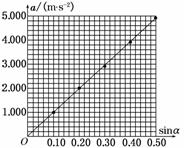
由mgsinα＝ma可得：a＝gsinα，故图线a－sinα的斜率即为当地的重力加速度．

由图可知，g＝k＝9.80 m/s².

(2)该探究小组采用的探究方法是控制变量法．