4．一小球从A点由静止开始做匀变速直线运动，若到达B点时速度为v，到达C点时速度

　 为2v，则AB∶BC等于　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　 A．1∶1　　 　　　 B．1∶2 　　　　　 C．1∶3　 　　　　 D．1∶4

3．自由落体第5个0.5 s经过的位移是第1个0.5 s经过的位移的倍数为　　　　 (　　 )

　　 A．5　　　　　 　　 B．9 　　　　　　 C．10　　　 　　　 D．25

2．a、b两个物体从同一地点同时出发，沿同一方向做匀变速直线运动，若初速度不同，加

　 速度相同，则在运动过程中　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　 ①a、b的速度之差保持不变　　　　　　 ②a、b的速度之差与时间成正比

　　 ③a、b的位移之差与时间成正比　　　　 ④a、b的位移之差与时间的平方成正比

　　 A．①③　 　　　　 B．①④　 　　　　 C．②③　　　　 　 D．②④　

1．做匀加速直线运动的物体的加速度为3 m/s²，对任意1 s来说，下列说法中不正确的是

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　 A．某1 s末的速度比该1 s初的速度总是大3 m/s

　　 B．某1 s末的速度比该1 s初的速度总是大3倍

　　 C．某1 s末的速度比前1 s末的速度大3 m/s

　　 D．某1 s末的速度比前1 s初的速度大6 m/s

16．(13分)如图所示，一半径为R的光滑绝缘半球面开口向下，固定在水平面上．整个空间存在磁感应强度为B、方向竖直向下的匀强磁场．一电荷量为q(q＞0)、质量为m的小球P在球面上做水平的匀速圆周运动，圆心为O′．球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0＜θ＜)．为了使小球能够在该圆周上运动，求磁感应强度B的最小值及小球P相应的速率．(已知重力加速度为g)

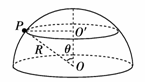
[解析]据题意可知，小球P在球面上做水平的匀速圆周运动，该圆周的圆心为O′．P受到向下的重力mg、球面对它沿OP方向的支持力FN和磁场的洛伦兹力f洛，则：

f洛＝qvB　(1分)

式中v为小球运动的速率，洛伦兹力f洛的方向指向O′

根据牛顿第二定律有：

FNcos θ－mg＝0　(2分)

f洛－FNsin θ＝m　(2分)

可得：v2－v+＝0　(2分) 源：高考%资源网 KS%5U]　　 源：高考%资源网 KS%5U]　　

由于v是实数，必须满足：

Δ＝()2－≥0　(2分)

由此得：B≥　(1分)

可见，为了使小球能够在该圆周上运动，磁感应强度B的最小值为：

Bmin＝

此时，带电小球做匀速圆周运动的速率为：

v＝　(2分)

解得：v＝sin θ．　(1分)

答案　sin θ

15．(11分)中国首个月球探测计划嫦娥工程预计在2017年送机器人上月球，实地采样送回地球，为载人登月及月球基地选址做准备．设想机器人随嫦娥号登月飞船绕月球飞行，飞船上备有以下实验仪器：

A．计时表一只；

B．弹簧秤一把；

C．已知质量为m的物体一个；

D．天平一台(附砝码一盒)．

在飞船贴近月球表面时可近似看成绕月球做匀速圆周运动，机器人测量出飞船在靠近月球表面的圆形轨道绕行N圈所用的时间为t．飞船的登月舱在月球上着陆后，遥控机器人利用所携带的仪器又进行了第二次测量，利用上述两次测量的物理量可出推导出月球的半径和质量．(已知引力常量为G)，要求：

(1)说明机器人是如何进行第二次测量的．

(2)试推导用上述测量的物理量表示的月球半径和质量的表达式．

[解析](1)机器人在月球上用弹簧秤竖直悬挂物体，静止时读出弹簧秤的示数F，即为物体在月球上所受重力的大小．　(3分)

(2)在月球上忽略月球的自转可知：

mg月＝F　(1分)

G＝mg月　(1分)

飞船在绕月球运行时，因为是靠近月球表面，故近似认为其轨道半径为月球的半径R，由万有引力提供物体做圆周运动的向心力可知：

G＝mR，又T＝　(2分)

联立可得：月球的半径R＝＝　(2分)

月球的质量M＝．　(2分)

[答案]　(1)机器人在月球上用弹簧秤竖直悬挂物体，静止时读出弹簧秤的示数F，即为物体在月球上所受重力的大小．

(2)R＝　M＝

14．(11分)若宇航员完成了对火星表面的科学考察任务，乘坐返回舱返回围绕火星做圆周运动的轨道舱，如图所示． 为了安全，返回舱与轨道舱对接时，必须具有相同的速度． 已知：该过程宇航员乘坐的返回舱至少需要获得的总能量为E(可看做是返回舱的初动能)，返回舱与人的总质量为m，火星表面重力加速度为g，火星半径为R，轨道舱到火星中心的距离为r，不计火星表面大气对返回舱的阻力和火星自转的影响． 问：

(1)返回舱与轨道舱对接时，返回舱与人共具有的动能为多少？

(2)返回舱在返回轨道舱的过程中，返回舱与人共需要克服火星引力做多少功？

[解析](1)在火星表面有：＝g　(2分)

　 设轨道舱的质量为m0，速度大小为v，则有 ：

G＝m0　(2分)

返回舱和人应具有的动能Ek＝mv2　(1分)

联立解得Ek＝．　 　(1分)

(2)对返回舱在返回过程中，由动能定理知：

W＝Ek－E 　(2分)

联立解得：火星引力对返回舱做的功W＝－E　(2分)

故克服引力做的功为：－W＝E－． 　(1分)

[答案]　(1)　(2)E－

13．(10分)火星和地球绕太阳的运动可以近似看做是同一平面内同方向的匀速圆周运动．已知火星公转轨道半径大约是地球公转轨道半径的．从火星、地球于某一次处于距离最近的位置开始计时，试估算它们再次处于距离最近的位置至少需多少地球年．[计算结果保留两位有效数字，＝1.85]

[解析]由G＝mr可知，行星环绕太阳运行的周期与行星到太阳的距离的二分之三次方成正比，即T∝r　

所以地球与火星绕太阳运行的周期之比为：

＝()＝()＝1.85　(3分)

设从上一次火星、地球处于距离最近的位置到再一次处于距离最近的位置，火星公转的圆心角为θ，则地球公转的圆心角必为2π+θ，它们公转的圆心角与它们运行的周期之间应有此关系：θ＝，θ+2π＝　(3分)

得：2π+＝　(2分)　 最后得：t＝＝T地≈2.2年　(2分)

[答案]　2.2

12．(8分)图甲为测量电动机转动角速度的实验装置，半径不大的圆形卡纸固定在电动机转轴上，在电动机的带动下匀速转动．在圆形卡纸的旁边安装一个改装了的电火花计时器．

下面是该实验的实验步骤：

①使电火花计时器与圆形卡纸保持良好接触；

②启动电动机，使圆形卡纸转动起来；

③接通电火花计时器的电源，使它工作起来；

④关闭电动机，拆除电火花计时器，研究卡纸上留下的一段痕迹(如图乙所示)，写出角速度ω的表达式，代入数据得出ω的测量值．

(1)要得到角速度ω的测量值，还缺少一种必要的测量工具，它是________．

A．秒表　B．游标卡尺　C．圆规　D．量角器

(2)写出ω的表达式，并指出表达式中各个物理量的含义：_____________________________________________________________________________．

(3)为了避免在卡纸连续转动的过程中出现打点重叠，在电火花计时器与盘面保持良好接触的同时，可以缓慢地将电火花计时器沿圆形卡纸半径方向向卡纸中心移动．这样，卡纸上打下的点的分布曲线不是一个圆，而是类似一种螺旋线，如图7－4丙所示．这对测量结果有影响吗？____________(填“有影响”或“没有影响”)理由是：____________________________________________________________________________________________________________________________________．

[解析](1)角速度ω＝，需量角器测量转过的夹角，故选项D正确．

(2)ω＝，θ是n个点的分布曲线所对应的圆心角，t是电火花计时器的打点时间间隔

(3)没有影响，因为电火花计时器向卡纸中心移动时不影响角度的测量．

[答案]　(1)D　(2分)

(2)ω＝，θ是n个点的分布曲线所对应的圆心角，t是电火花计时器的打点时间间隔　(3分)

(3)没有影响　(1分)　电火花计时器向卡纸中心移动时不影响角度的测量　(2分)

0.48＝v0t2　 解得：v0＝1.6 m/s．

(2)由图可知，物体由A→B和由B→C所用的时间相等，且有：Δy＝gT2

x＝v0T解得：v0＝1.5 m/s，vBy＝＝2 m/s．

[答案]　(1)1.6　(2分)　(2)1.5　(3分)　2　(2分)