3．某同学做“探究弹力和弹簧伸长量的关系”实验，他先把弹簧平放在桌面上使其自然伸长，用直尺测出弹簧的原长L₀，再把弹簧竖直悬挂起来，挂上砝码后测出弹簧伸长后的长度L，把L－L₀作为弹簧的伸长量x，这样操作，由于弹簧自身重力的影响，最后画出的图线可能是下图的哪一个　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

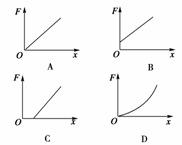
[答案]　C

[解析]　原长的测量值小于真实值，设误差为Δl，弹簧的实际伸长量x′＝x－Δl，弹力与伸长量成正比，即F＝k(x－Δl)，所以最后的图线是C.

2．下面列出的措施中，哪些是有利于改进本实验结果的　　　　　　　　　　　　　　　　 (　)

A．橡皮条弹性要好，拉到O点时拉力要适当大一些

B．两个分力F₁和F₂间的夹角要尽量大一些

C．拉橡皮条时，橡皮条、细绳和弹簧秤平行贴近木板面

D．拉橡皮条的绳要细，而且要稍长一些

[答案]　ACD

[解析]　拉力“适当”大一些能减小误差；而夹角“尽量”大一些，则使作图误差变大；橡皮条等“贴近”木板，目的是使拉线水平；绳子要细且稍长便于确定力的方向．

1．在“探究弹力和弹簧伸长的关系”的实验中，如何保证刻度尺竖直　　　　　　 (　)

A．使用三角板　　　　　 B．使用重垂线

C．目测　 　　　　　　　　　　　　　　　　 D．不用检查

[答案]　B

[解析]　使用重垂线可保证刻度尺竖直，故B正确．A、C不准确，不合题意，D是错误的．

13．“翻滚过山车”的物理原理可以用如图所示装置演示，光滑斜槽轨道AD与半径为R＝0.1 m的竖直圆轨道(圆心为O)相连，AD与圆O相切于D点，B为轨道的最低点，∠DOB＝37°.质量为m＝0.1 kg的小球从距D点L＝1.3 m处由静止开始下滑，然后冲上光滑的圆形轨道(g＝10 m/s²，sin37°＝0.6，cos37°＝0.8)．求：

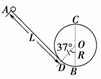
(1)小球在光滑斜槽轨道上运动的加速度的大小；

(2)小球通过B点时对轨道的压力的大小；

(3)试分析小球能否通过竖直圆轨道的最高点C，并说明理由．

[答案]　(1)6m/s²　(2)17N　(3)能

[解析]　(1)在光滑斜槽上由牛顿第二定律得：

mgsin37°＝ma.

故a＝gsin37°＝6m/s²

(2)小球由A至B，机械能守恒，则

mg(Lsin37°+h_DB)＝mv

h_DB＝R(1－cos37°)

又小球在B点，由牛顿第二定律得：

F_NB＝mg+m＝17N

由牛顿第三定律得：小球过B点时对轨道的压力大小为17N.

(3)小球要过最高点，需要的最小速度为v₀

则mg＝m

即v₀＝＝1m/s

又小球从A到C机械能守恒，所以

mg[Lsin37°－R(1+cos37°)]＝mv

解之v_C＝m/s>1m/s

故小球能过最高点C.

12．(2009·温州模拟)在如图所示的装置中，两个光滑的定滑轮的半径很小，表面粗糙的斜面固定在地面上，斜面的倾角为θ＝30°.用一根跨过定滑轮的细绳连接甲、乙两物体，把甲物体放在斜面上且连线与斜面平行，把乙物体悬在空中，并使悬线拉直且偏离竖直方向α＝60°.现同时释放甲、乙两物体，乙物体将在竖直平面内振动，当乙物体运动经过最高点和最低点时，甲物体在斜面上均恰好未滑动．已知乙物体的质量为m＝1kg，若取重力加速度g＝10m/s².试求：

(1)乙物体运动经过最高点和最低点时悬绳的拉力大小；

(2)甲物体的质量及斜面对甲物体的最大静摩擦力．

[答案]　(1)5N　20N　(2)2.5kg　7.5N

[解析]　(1)设乙物体运动到最高点时，绳子上的弹力为F_T1.

对乙物体F_T1＝mgcosα＝5N

当乙物体运动到最低点时，绳子上的弹力为F_T2

对乙物体由机械能守恒定律：mgl(1－cosα)＝mv²

又由牛顿第二定律：F_T2－mg＝m

得：F_T2＝mg(3－2cosα)＝20N.

(2)设甲物体的质量为M，所受的最大静摩擦力为F_f，乙在最高点时甲物体恰好不下滑，有：Mgsinθ＝F_f+FT₁

得：Mgsinθ＝F_f+mgcosα

乙在最低点时甲物体恰好不上滑，有：Mgsinθ+F_f＝FT₂

得：Mgsinθ+F_f＝mg(3－2cosα)

可解得：M＝＝2.5kg

F_f＝mg(1－cosα)＝7.5N.

11．如图所示，一可视为质点的物体质量为m＝1kg，在左侧平台上水平抛出，恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道，并沿轨道下滑，A、B为圆弧两端点，其连线水平，O为轨道的最低点．已知圆弧半径为R＝1.0m，对应圆心角为θ＝106°，平台与AB连线的高度差为h＝0.8m.(重力加速度g＝10m/s²，sin53°＝0.8，cos53°＝0.6)求：

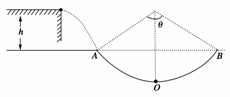
(1)物体平抛的初速度；

(2)物体运动到圆弧轨道最低点O时对轨道的压力．

[答案]　(1)3m/s　(2)43 N

[解析]　(1)由于物体无碰撞进入圆弧轨道，即物体落到A点时速度方向沿A点切线方向，则tanα＝＝＝tan53°　 　　　　　　　　　　　　　　　　　　　　　　　　 ①

又由h＝gt² ②

而v_y＝gt.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

联立以上各式得v₀＝3m/s　　　　　　　　　　　　　　　　　　　　　　　　　　 ④

(2)设物体到最低点的速度为v，由机械能守恒，有

mv²－mv＝mg[h+R(1－cos53°)]　　　　　　　　　　　　　　　　　　　 ⑤

在最低点，据牛顿第二定律，有

F_N－mg＝m　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑥

代入数据解得F_N＝43N　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑦

由牛顿第三定律可知，物体对轨道的压力为43N.　　　　　　　　 ⑧

10．一半径为R的雨伞绕伞柄以角速度ω匀速转动，如图所示，伞边缘距地面高为h，甩出的水滴做平抛运动，在地面上形成一个圆，求此圆半径r为多少？

[答案]　R

[解析]　水滴从伞边缘甩出去以后做平抛运动，水滴在空中做平抛运动的时间是：

t＝

水平方向的位移为：s＝v₀t＝ωR

可见水滴落在地面上形成的圆半径为

r²＝R²+S²　r＝R.

9．如图所示，直径为d的纸制圆筒以角速度ω绕垂直纸面的轴O匀速转动(图示为截面)．从枪口发射的子弹沿直径穿过圆筒．若子弹在圆筒旋转不到半周时，在圆周上留下a、b两个弹孔，已知aO与bO夹角为θ，求子弹的速度．

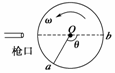
[答案]　

[解析]　子弹射出后沿直线运动，从a点射入，从b点射出，该过程中圆筒转过的角度为π－θ..

设子弹速度为v，则子弹穿过筒的时间t＝

此时间内筒转过的角度α＝π－θ

据α＝ωt得，π－θ＝ω

则子弹速度v＝

8．(2009·威海调研考试)如图所示，M为固定在水平桌面上的有缺口的方形木块，abcd为圆周的光滑轨道，a为轨道的最高点，de面水平且有一定长度．今将质量为m的小球在d点的正上方高为h处由静止释放，让其自由下落到d处切入轨道内运动，不计空气阻力，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

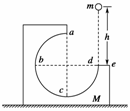
A．在h一定的条件下，释放后小球的运动情况与小球的质量有关

B．改变h的大小，就能使小球通过a点后，落回轨道内

C．无论怎样改变h的大小，都不可能使小球通过b点后落回轨道内

D．调节h的大小，使小球飞出de面之外(即e的右面)是可能的

[答案]　D

[解析]　在h一定的条件下，释放后小球的运动情况与小球的质量无关，A错；当小球运动到a点时，临界条件是木块对小球的支持力为零，则mg＝

即v＝，R＝gt²

即t＝　∴s＝vt＝R>R，

∴改变h的大小，不能使小球通过a点后，落回轨道内，B错，D对；而改变h的大小，可能使小球通过b点后落回轨道内，C错，故答案选D.

7．(2010·泰州市联考)如图所示，半径为R的竖直光滑圆轨道内侧底部静止着一个光滑小球，现给小球一个冲击使其在瞬间得到一个水平初速度v₀，若v₀大小不同，则小球能够上升到的最大高度(距离底部)也不同．下列说法中正确的是　　 　　　　　　　　　　　　　　　　　 (　)

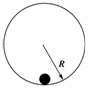
A．如果v₀＝，则小球能够上升的最大高度为

B．如果v₀＝，则小球能够上升的最大高度为

C．如果v₀＝，则小球能够上升的最大高度为

D．如果v₀＝，则小球能够上升的最大高度为2R

[答案]　AD

[解析]　根据机械能守恒定律，当速度为v₀＝，由mgh＝mv解出h＝，A项正确，B项错误；当v₀＝，小球正好运动到最高点，D项正确；当v₀＝时小球运动到最高点以下，若C项成立，说明小球此时向心力为0，这是不可能的．