10．如图13所示，在倾角为θ的光滑斜面上有两个用轻质弹簧相连接的物块A、B，它们的质量分别为m_A、m_B，弹簧的劲度系数为k，C为一固定挡板，系统处于静止状态．现开始用一恒力F沿斜面方向拉物块A使之向上运动，求物块B刚要离开C时物块A的加速度a和从开始到此时物块A的位移d.重力加速度为g.

解析：令x₁表示未加F时弹簧的压缩量，由胡克定律和牛顿定律可知

kx₁＝m_Agsinθ①

令x₂表示B刚要离开C时弹簧的伸长量，a表示此时A的加速度，由胡克定律和牛顿定律可知

kx₂＝m_Bgsinθ②

F－m_Agsinθ－kx₂＝m_Aa③

由②③式可得a＝④

由题意　d＝x₁+x₂⑤

由①②⑤式可得d＝.

答案：a＝　d＝

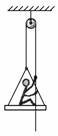
图14

图11

9．有5个质量均为m的相同木块，并列地放在水平地面上，如图11所示，已知木块与地面间的动摩擦因数为μ，当木块1受到水平力F的作用时，5个木块同时向右做匀加速运动，求：

(1)匀加速运动的加速度．

(2)第4块木块所受合力．

(3)第4块木块受到第3块木块作用力的大小．

解析：(1)选5个木块组成的系统为研究对象，设每一木块受到的滑动摩擦力为F_f，则系统所受外力的合力是：

F_合＝F－5F_f＝F－5μmg

系统的质量是5m，由牛顿第二定律得：F－5μmg＝5ma

故系统的加速度是a＝＝－μg

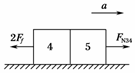
图12

(2)选第4块木块为研究对象，由牛顿第二定律可直接求得合力F_4合＝ma＝－μmg

(3)选第4、第5两木块组成的系统为研究的对象，水平受力如图12所示，由牛顿第二定律得：F_N34－2F_f＝2ma，故第4块木块受到第3块木块的作用力为：F_N34＝2ma+2F_f＝2m(－μg)+2μmg＝F

答案：(1)－μg　(2)－μmg　(3)F

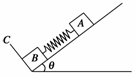
图13

8．如图10所示，竖直放置在水平面上的轻质弹簧上叠放着两物块A、B，A、B的质量均为2 kg，它们处于静止状态．若突然将一个大小为10 N，方向竖直向下的力施加在物块A上，则此瞬间，A对B的压力大小为：(g＝10 m/s²)(　)

A．10 N　 　　　　　　　　　　　　　　　　　　　　 B．20 N

C．25 N　 　　　　　　　　　　　　　　　　　　　　 D．30 N

解析：对AB整体分析，当它们处于静止状态时，弹簧的弹力等于整体AB的重力，当施加力F的瞬间，弹力在瞬间不变，故A、B所受合力为10 N，则a＝F_合/(2m)＝2.5 m/s²，后隔离A物块受力分析，得F+mg－F_N＝ma，解得F_N＝25 N，所以A对B的压力大小也等于25 N.

答案：C

7．如图9所示，质量为M的框架放在水平地面上，一轻弹簧上端固定在框架上，下端固定一个质量为m的小球，小球上下振动时，框架始终没有跳起，当框架对地面压力为零瞬间，小球的加速度大小为(　)

A．g　　　　　　　　　　　　　　 B.g

C．0　 　　　　　　　　　　　　　　　　　　　　　　 D.g

解析：弹簧的弹力与框架的重力平衡，故小球受的合外力为(M+m)g.对m由牛顿第二定律得：(M+m)g＝ma，所以该瞬间a＝g.

答案：D

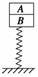
图10

6．如图8所示，一轻绳通过一光滑定滑轮，两端各系一质量分别为m₁和m₂的物体，m₁放在地面上，当m₂的质量发生变化时，m₁的加速度a的大小与m₂的关系图象大体如下图中的(　)

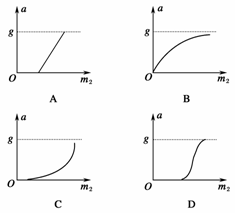
答案：D

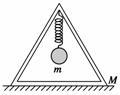
图9

5．如图7所示，质量为m₁和m₂的两个物体用细线相连，在大小恒定的拉力F作用下，先沿水平面，再沿斜面(斜面与水平面成θ角)，最后竖直向上运动．则在这三个阶段的运动中，细线上张力的大小情况是(　)

A．由大变小　 　　　　　　　　　　　　　　　　 B．由小变大

C．始终不变　 　　　　　　　　　　　　　　　　 D．由大变小再变大

解析：设细线上的张力为F₁.要求F₁，选受力少的物体m₁为研究对象较好；此外还必须知道物体m₁的加速度a，要求加速度a，则选m₁、m₂整体为研究对象较好．

在水平面上运动时：

F₁－μm₁g＝m₁a①

F－μ(m₁+m₂)g＝(m₁+m₂)a②

联立①②解得：F₁＝

在斜面上运动时：

F₁－m₁gsinθ－μm₁gcosθ＝m₁a③

F－(m₁+m₂)gsinθ－μ(m₁+m₂)gcosθ＝(m₁+m₂)a④

联立③④解得：F₁＝

同理可得，竖直向上运动时，细线上的张力F₁仍是

答案：C

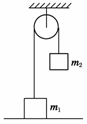
图8

4．在一正方形小盒内装一小圆球，盒与球一起沿倾角为θ的光滑斜面下滑，如图5所示．若不计摩擦，当θ角增大时，下滑过程圆球对方盒前壁压力F_N及对方盒底面的压力F_N′将如何变化(　)

A．F_N′变小，F_N变小

B．F_N′变小，F_N为零

C．F_N′变小，F_N变大

D．F_N′不变，F_N变大

解析：

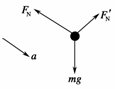
图6

系统(球和小盒)在垂直于斜面方向无加速度，该方向合外力为零．对小球有：F_N′＝mgcosθ，故当θ增大时，F_N′变小．在平行于斜面方向的加速度a＝gsinθ，在该方向物体处于“完全失重”状态，所以小球对小盒前壁的压力F_N始终为零，与θ大小无关．

答案：B

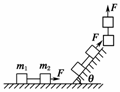
图7

3．如图4所示，在光滑水平面上有两个质量分别为m₁和m₂的物体A、B，m₁>m₂，A、B间水平连接着一轻质弹簧秤．若用大小为F的水平力向右拉B，稳定后B的加速度大小为a₁，弹簧秤示数为F₁；如果改用大小为F的水平力向左拉A，稳定后A的加速度大小为a₂，弹簧秤示数为F₂.则以下关系式正确的是(　)

A．a₁＝a₂，F₁>F₂　　　　　　　　 B．a₁＝a₂，F₁<F₂

C．a₁<a₂，F₁＝F₂　 　　　　　　　　　　　　 D．a₁>a₂，F₁>F₂

解析：整体法分析，无论用F拉A，还是拉B，F＝(m₁+m₂)a均成立，所以稳定后A的加速度a₁和B的加速度a₂相等．F拉B时，对A分析，F₁＝m₁a，F拉A时，对B分析，F₂＝m₂a，因m₁>m₂，故F₁>F₂，所以选项A正确．

答案：A

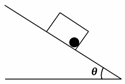
图5

2．如图3所示，在光滑水平面上叠放着A、B两物体，已知m_A＝6 kg、m_B＝2 kg，A、B间动摩擦因数μ＝0.2，在物体A上系一细线，细线所能承受的最大拉力是20 N，现水平向右拉细线，g取10 m/s²，则(　)

A．当拉力F<12 N时，A静止不动

B．当拉力F>12 N时，A相对B滑动

C．当拉力F＝16 N时，B受A的摩擦力等于4 N

D．无论拉力F多大，A相对B始终静止

解析：设A、B共同运动时的最大加速度为a_max，最大拉力为F_max

对B：μm_Ag＝m_Ba_max，a_max＝＝6 m/s²

对A、B：F_max＝(m_A+m_B)a_max＝48 N

当F<F_max＝48 N时，A、B相对静止．

因为地面光滑，故A错，当F大于12 N而小于48 N时，A相对B静止，B错．

当F＝16 N时，其加速度a＝2 m/s².

对B：F_f＝4 N，故C对．

因为细线的最大拉力为20 N，所以A、B总是相对静止，D对．

答案：CD

图4

1．如图1，在倾角为α的固定光滑斜面上，有一用绳子拴着的长木板，木板上站着一只猫．已知木板的质量是猫的质量的2倍．当绳子突然断开时，猫立即沿着板向上跑，以保持其相对斜面的位置不变．则此时木板沿斜面下滑的加速度为(　)

A.sinα　　　　　　　　　　　 B．gsinα

C.gsinα　 　　　　　　　　　　　　　　　　　　　　 D．2gsinα

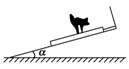
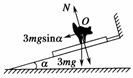
图1　　　　　　　　　　　 图2

解析：当绳子突然断开，猫保持其相对斜面的位置不变，即相对地面位置不变，猫可视为静止状态，木板沿斜面下滑，取猫和木板整体为研究对象，如图2进行受力分析，由牛顿第二定律得3mgsinα＝2ma，a＝gsinα，所以C选项正确．

答案：C

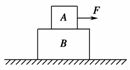
图3