
题目列表(包括答案和解析)
11.曾经流行过一种自行车车头灯供电的小型交流发电机,图8甲为其结构示意图.图中N、S是一对固定的磁极,abcd为固定转轴上的矩形线框,转轴过bc边中点,与ab边平行,它的一端有一半径r0=1.0 cm的摩擦小轮,小轮与自行车车轮的边缘相接触,如图8乙所示.当车轮转动时,因摩擦而带动小轮转动,从而使线框在磁极间转动.设线框由N=800匝导线圈组成,每匝线圈的面积S=20 cm2,磁极间的磁场可视作匀强磁场,磁感应强度B=0.010 T,自行车车轮的半径R1=35 cm,小齿轮的半径R2=4.0 cm,大齿轮的半径R3=10.0 cm.现从静止开始使大齿轮加速转动,问大齿轮的角速度为多大才能使发电机输出电压的有效值U=3.2 V?(假设摩擦小轮与自行车车轮之间无相对滑动)

图8
解析:当自行车车轮转动时,通过摩擦小轮使发电机的线框在匀强磁场内转动,线框中产生一正弦交流电动势,旋转线框与摩擦小轮角速度相等,而摩擦小轮又与车轮线速度相等(自行车车轮与摩擦小轮之间无相对滑动),车轮又与小齿轮角速度相等,最终小齿轮与大齿轮边缘的线速度相等,由此得解.
答案:旋转线框产生感应电动势的峰值Em=NBSω0
式中ω0为线框转动的角速度,即摩擦小轮转动的角速度.
发电机两端电压的有效值U=Em/2
设自行车车轮转动的角速度为ω1,有R1ω1=r0ω0
小齿轮转动的角速度与自行车车轮转动的角速度相同,均为ω1,设大齿轮转动的角速度为ω,有R3ω=R2ω1
由以上各式解得ω=(UR2r0)/(NBSR3R1)
代入数据得ω=3.2 rad/s.
10.如图7所示,矩形线圈abcd在磁感应强度B=2 T的匀强磁场中绕轴OO′以角速度ω=10π rad/s匀速转动,线圈共10匝,每匝线圈的电阻值为0.5 Ω,ab=0.3 m,bc=0.6 m,负载电阻R=45 Ω.求
(1)电阻R在0.05 s内发出的热量;
(2)电阻R在0.05 s内流过的电荷量(设线圈从垂直中性面开始转动).
解析:(1)矩形线圈abcd在匀强磁场中旋转产生正弦交变电流,电动势的峰值为Em=nBSω=10×2×0.3×0.6×10π=113.04 V,电流的有效值I===1.60 A
Q=I2Rt=5.76 J
(2)矩形线圈旋转过程中产生的感应电动势的平均值E=n====72 V,电流的平均值I==1.44 A;0.05 s内电路流过的电荷量q=It=0.072 C.
答案:(1)5.76 J (2)0.072 C
9.用均匀导线弯成正方形闭合线框abcd,线框每边长10 cm,每边的电阻值为0.1 Ω.把线框放在磁感应强度为B=0.1 T的匀强磁场中,并使它绕轴O1O2以ω=100 rad/s的角速度旋转,旋转方向如图6所示(沿O2O1由O2向O1看为顺时针方向).已知O1、O2两点分别在ad和bc上,轴O1O2在线框平面内,并且垂直于B,O1d=3O1a,O2c=3O2b.
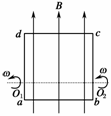
图6
(1)当线框平面转至和B平行的瞬时(如图6所示位置)
①每个边产生的感应电动势的大小各是多少?
②线框内感应电流的大小是多少?方向如何?
(2)求线框由图所示位置旋转的过程中产生的平均电动势的大小;
(3)线框旋转一周内产生的热量为多少?
解析:(1)①令L表示正方形线框的边长,R表示其每边的电阻值,则L=0.1 m,R=0.1 Ω,设此时cd段感应电动势的大小为E1,ab段感应电动势的大小为E2,则
E1=BLv1=3BL2ω/4=0.075 V
E2=BLv2=BL2ω/4=0.025 V
da段和bc段不切割磁感线,所以它们的电动势都是零
②线框中的感应电动势E=E1+E2=0.1 V线框中的感应电流为I=E/(4R)=0.25 A
根据楞次定律或右手定则,可判断电流方向沿dcbad
(2)根据法拉第电磁感应定律,线框由图所示位置旋转的过程中产生的平均电动势的大小,E==== V=0.083 V
(3)线框旋转一周产生的热量为Q=()2R总T=()24R=2.5π×10-4 J=7.85×10-4 J
答案:(1)①Ecd=0.075 V Eab=0.025 V Eda=Ebc=0
②I=0.25 A 方向沿dcbad (2)0.083 V (3)7.85×10-4 J
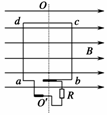
图7
8.如图5所示,图线a是线圈在匀强磁场中匀速转动时所产生的正弦交流电的图象,当调整线圈转速后,所产生正弦交流电的图象如图线b所示,以下关于这两个正弦交流电的说法正确的是( )
A.线圈先后两次转速之比为3∶2
B.两种情况在0.3 s内通过线圈的磁通量之比为1∶1
C.两种情况在相等时间内产生的焦耳热之比Qa∶Qb=3∶2
D.两种情况在相等时间内产生的焦耳热之比Qa∶Qb=9∶4
解析:两种情况Ta∶Tb=2∶3,fa∶fb=3∶2,线圈先后两次转速之比为3∶2,选项A正确.两种情况下在0.3 s内磁通量的变化量不同,选项B错误.交流电的最大值Em=NBSω,电动势最大值之比为3∶2.Q=t,两种情况在相等时间内产生的焦耳热之比Qa∶Qb=9∶4,选项D正确.
答案:AD
0.02 C,D正确.
答案:AD

图5
7.如图4所示,边长为L=0.2 m的正方形线圈abcd,其匝数为n=10、总电阻为r=2 Ω,外电路的电阻为R=8 Ω,ab的中点和cd的中点的连线OO′恰好位于匀强磁场的边界线上,磁场的磁感应强度B=1 T,若线圈从图示位置开始,以角速度ω=2 rad/s绕OO′轴匀速转动,则以下判断中正确的是( )
A.在t=时刻,磁场穿过线圈的磁通量为零,但此时磁通量随时间变化最快
B.闭合电路中感应电动势的瞬时表达式e=0.8 sin2t V
C.从t=0时刻到t=时刻,电阻R上产生的热量为Q=3.2π×10-4 J
D.从t=0时刻到t=时刻,通过R的电荷量q=0.02 C
解析:线圈在磁场中转动,Em=nBSω=0.4 V,B错.当线圈平面与磁场平行时磁通量变化最快,A正确.QR=I2Rt
=2Rt=1.6π×10-3 J,C错.q=n=
6.如图3所示,矩形线圈abcd,面积为S,匝数为N,线圈电阻为R,在匀强磁场中可以分别绕垂直于磁场方向的轴P1和P2以相同的角速度ω匀速转动,(P1以ab边为轴,P2以ad边中点为轴)当线圈平面从与磁场方向平行开始计时,线圈转过90°的过程中,绕P1及P2轴转动产生的交流电的电流大小,电荷量及焦耳热分别为I1,q1,Q1及I2,q2,Q2,则下面判断正确的是( )
A.线圈绕P1和P2转动时电流的方向相同,都是a→b→c→d
B.q1>q2=NBS/2R
C.I1=I2=(NBωS)/R
D.Q1<Q2=πω(NBS)2/2R
解析:本题考查电磁感应中电荷量、热量、电流的计算和感应电流方向的判断.绕P1、P2转动时电流的方向相同,但电流的方向为a→d→c→b→a,A错;电荷量q=,与绕哪个轴转动没有关系,B错;线圈绕两轴转动时产生的电动势相同,所以电流相同,发热也相同,C对D错.
答案:C
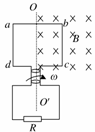
图4
5.一单匝闭合线框在匀强磁场中绕垂直于磁场方向的转轴匀速转动.在转动过程中,线框中的最大磁通量为Φm,最大感应电动势为Em,下列说法中正确的是( )
A.当磁通量为零时,感应电动势也为零
B.当磁通量减小时,感应电动势也减小
C.当磁通量等于0.5Φm时,感应电动势等于0.5Em
D.角速度ω等于Em/Φm
解析:根据正弦式电流的产生及其变化规律:当磁通量最大时,感应电动势为零;当磁通量减小时,感应电动势在增大;磁通量减为零时,感应电动势最大.由此可知A、B项错误.设从线框位于中性面开始计时,则有e=Emsinωt,式中Em=BSω.因Φm=BS,故角速度ω=,D项正确.设e=0.5Em,则解出ωt=π/6.此时Φ=B·Scos=BS=Φm,所以C项错.
答案:D

图3
4.如图2所示,矩形线框置于竖直向下的磁场中,通过导线与灵敏电流表相连,线框在磁场中绕垂直于磁场方向的转轴匀速转动,图中线框平面处于竖直面内,下述说法正确的是( )
A.因为线框中产生的是交变电流,所以电流表示数始终为零
B.线框通过图中位置瞬间,穿过线框的磁通量最大
C.线框通过图中位置瞬间,通过电流表的电流瞬时值最大
D.若使线框转动的角速度增大一倍,那么通过电流表电流的有效值也增大一倍
解析:本题考查电磁感应现象,基础题.线框在匀强磁场中匀速转动时,在中性面即线框与磁感线垂直时,磁通量最大感应电动势最小,而在题中图示位置线框与磁感应线平行时,磁通量最小感应电动势最大,A、B错C对;电流的有效值I=,现在其余的量都不变,角速度增大一倍后,电流也增大一倍,D正确.
答案:CD
3.如下图中各图面积均为S的线圈均绕其对称轴或中心轴在匀强磁场B中以角速度ω匀速转动,能产生正弦交变电动势e=BSωsinωt的图是( )

解析:线圈在匀强磁场中绕垂直于磁场方向的轴(轴在线圈所在平面内)匀速转动,产生的正弦交变电动势为e=BSωsinωt,由这一原则判断,A图和C图中感应电动势均为e=BSωsinωt;B图中的转动轴不在线圈所在平面内;D图转动轴与磁场方向平行,而不是垂直.
答案:AC
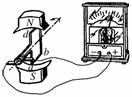
图2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com