6．如图6所示，在屏MN的上方有磁感应强度为B的匀强磁场，磁场方向垂直纸面向里．P为屏上的一小孔，PC与MN垂直．一群质量为m 、带电荷量为－q的粒子(不计重力)，以相同的速率v，从P处沿垂直于磁场的方向射入磁场区域．粒子入射方向在与磁场B垂直的平面内，且散开在与PC夹角为θ的范围内．则在屏MN上被粒子打中的区域的长度为(　)

图6

A.　 　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　 D.

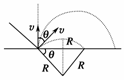
图7

解析：能打到的范围中最远点为2R处，其中R为轨迹半径，R＝，最近点为2Rcosθ处，所以总长度L＝2R－2Rcosθ＝.

答案：D

图8

5．如图4所示，在半径为R的圆形区域内有匀强磁场．在边长为2R的正方形区域里也有匀强磁场，两个磁场的磁感应强度大小相同．两个相同的带电粒子以相同的速率分别从M、N两点射入匀强磁场．在M点射入的带电粒子，其速度方向指向圆心；在N点射入的带电粒子，速度方向与边界垂直，且N点为正方形边长的中点，则下列说法正确的是(　)

图4

A．带电粒子在磁场中飞行的时间可能相同

B．从M点射入的带电粒子可能先飞出磁场

C．从N点射入的带电粒子可能先飞出磁场

D．从N点射入的带电粒子不可能比M点射入的带电粒子先飞出磁场

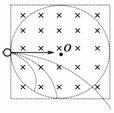
图5

解析：画轨迹草图如图5所示，容易得出粒子在圆形磁场中的轨迹长度(或轨迹对应的圆心角)不会大于在正方形磁场中的，故A、B、D正确．

答案：ABD

4．如图3所示是电视机中显像管的偏转线圈示意图，它由绕在磁环上的两个相同的线圈串联而成，线圈中通有如图3所示方向的电流．当电子束从纸里经磁环中心向纸外射来时(图中用符号“·”表示电子束)．它将(　)

A．向上偏转　　　　　　　　　　 B．向下偏转

C．向右偏转　 　　　　　　　　　　　　　　　　 D．向左偏转

解析：由右手定则判断在偏转线圈内部存在水平向左的磁场，再由左手定则判定电子束向上偏转．

答案：A

3．如图2所示，水平导线中有电流I通过，导线正下方的电子初速度的方向与电流I的方向相同，则电子将(　)

A．沿路径a运动，轨迹是圆

B．沿路径a运动，轨迹半径越来越大

C．沿路径a运动，轨迹半径越来越小

D．沿路径b运动，轨迹半径越来越小

解析：由r＝知B减小，r越来越大，故电子的径迹是a.

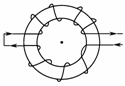
图3

答案：B

2．质子(p)和α粒子以相同的速率在同一匀强磁场中做匀速圆周运动，轨道半径分别为R_p和R_α，周期分别为T_p和T_α.则下列选项正确的是(　)

A．R_p∶R_α＝1∶2　T_p∶T_α＝1∶2

B．R_p∶R_α＝1∶1　T_p∶T_α＝1∶1

C．R_p∶R_α＝1∶1　T_p∶T_α＝1∶2

D．R_p∶R_α＝1∶2　T_p∶T_α＝1∶1

解析：由洛伦兹力提供向心力，则qvB＝m，R＝，由此得：＝·＝·＝

由周期T＝得：＝·＝＝，故A选项正确．

答案：A

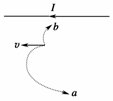
图2

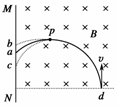
图1

1．如图1所示，匀强磁场的方向垂直纸面向里，一带电微粒从磁场边界d点垂直于磁场方向射入，沿曲线dpa打到屏MN上的a点，通过pa段用时为t，若该微粒经过p点时，与一个静止的不带电微粒碰撞并结合为一个新微粒，最终打到屏MN上．两个微粒所受重力均忽略．新微粒运动的(　)

A．轨迹为pb，至屏幕的时间将小于t

B．轨迹为pc，至屏幕的时间将大于t

C．轨迹为pb，至屏幕的时间将等于t

D．轨迹为pa，至屏幕的时间将大于t

解析：碰撞过程其动量守恒，所以碰撞前后动量不变．由r＝知，微粒的轨道半径不变，故其轨迹仍为pa，但由于碰后其运动速率比原来小，所以至屏幕时间将大于t.

答案：D

11．(2009·辽宁/宁夏高考)如图11所示，在第一象限有一匀强电场，场强大小为E，方向与y轴平行；在x轴下方有一匀强磁场，磁场方向与纸面垂直．一质量为m、电荷量为－q(q>0)的粒子以平行于x轴的速度从y轴上的P点处射入电场，在x轴上的Q点处进入磁场，并从坐标原点O离开磁场．粒子在磁场中的运动轨迹与y轴交于M点．已知OP＝l，OQ＝2l.不计重力．求：

(1)M点与坐标原点O间的距离；

(2)粒子从P点运动到M点所用的时间．

解析：

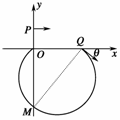
图12

(1)带电粒子在电场中做类平抛运动，沿y轴负方向上做初速度为零的匀加速运动，设加速度的大小为a；在x轴正方向上做匀速直线运动，设速度为v₀；粒子从P点运动到Q点所用的时间为t₁，进入磁场时速度方向与x轴正方向夹角为θ，则

a＝①

t₁＝②

v₀＝③

其中x₀＝2l，y₀＝l.又有tanθ＝④

联立②③④式，得θ＝30°⑤

因为M、O、Q点在圆周上，∠MOQ＝90°，所以MQ为直径．从图中的几何关系可知，

R＝2l⑥

MO＝6l⑦

(2)设粒子在磁场中运动的速度为v，从Q到M点运动的时间为t₂，则有

v＝⑧

t₂＝⑨

带电粒子自P点出发到M点所用的时间t为

t＝t₁+t₂⑩

联立①②③⑤⑥⑧⑨⑩式，并代入数据得

t＝ ⑪

答案：(1)6l　(2)

10．如图10所示，Oxyz坐标系的y轴竖直向上，在坐标系所在的空间存在匀强电场和匀强磁场，电场方向与x轴平行．从y轴上的M点(0，H,0)无初速释放一个质量为m、电荷量为q的带负电的小球，它落在xz平面上的N(L,0，b)点(L>0，b>0)．若撤去磁场则小球落在xz平面的P点(L,0,0)．已知重力加速度为g.

(1)已知匀强磁场方向与某个坐标轴平行，试判断其可能的具体方向；

(2)求电场强度E的大小；

(3)求小球落至N点时的速率v.

解析：(1)用左手定则判断出：磁场方向为－x方向或－y方向．

(2)在未加匀强磁场时，带电小球在电场力和重力作用下落到P点，设运动时间为t，小球自由下落，有H＝gt²

小球沿x轴方向只受电场力作用F_E＝qE

小球沿x轴的位移为L＝at²

小球沿x轴方向的加速度a＝

联立求解，得：E＝

(3)带电小球在匀强磁场和匀强电场共存的区域运动时，洛仑兹力不做功电场力做功为W_E＝qEL

重力做功为W_G＝mgH

设落到N点速度大小为v，根据动能定理有mgH+qEL＝mv²

解得v＝

答案：(1)－x方向或－y方向　(2)

(3)

图11

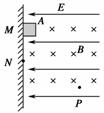
图8

9．如图8所示，水平向左的匀强电场E＝4 V/m，垂直纸面向里的匀强磁场B＝2 T，质量m＝1 g的带正电的小物块A，从M点沿绝缘粗糙的竖直壁无初速滑下，滑行0.8 m到N点时离开竖直壁做曲线运动，在P点时小物块A瞬时受力平衡，此时速度与水平方向成45°.若P与N的高度差为0.8 m，求：

(1)A沿壁下滑过程中摩擦力所做的功；

(2)P与N的水平距离．

解析：分清运动过程，应用动能定理列式求解．

(1)物体在N点时，墙对其弹力为零，水平方向Eq＝qvB，

所以v＝＝2 m/s，由M→N过程据动能定理：

mg+W_f＝mv²－0，所以W_f＝－6×10^－3 J.

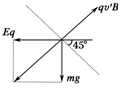
图9

(2)设在P点速度为v′其受力如图9所示，所以Eq＝mg，qv′B＝Eq，得v′＝2 m/s.

设N、P水平距离x，竖直距离y，物体由N→P过程电场力和重力做功，由动能定理

mgy－Eq·x＝mv′²－mv²，得x＝0.6 m.

答案：(1)－6×10^－3 J　(2)0.6 m

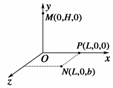
图10

8．目前，世界上正在研究一种新型发电机叫磁流体发电机．如图7表示了它的原理：将一束等离子体喷射入磁场，在场中有两块金属板A、B，这时金属板上就会聚集电荷，产生电压．如果射入的等离子体速度均为v，两金属板的板长为L，板间距离为d，板平面的面积为S，匀强磁场的磁感应强度为B，方向垂直于速度方向，负载电阻为R，电离气体充满两板间的空间．当发电机稳定发电时，电流表示数为I.那么板间电离气体的电阻率为(　)

A.(－R)　 　　　　　　　　　　　　　　　　 B.(－R)

C.(－R)　 　　　　　　　　　　　　　　　　 D.(－R)

解析：当粒子受的电场力与洛伦兹力平衡时，两板电压即为电动势，即qvB＝q，得U＝Bdv.

又I＝，r＝ρ

由此可解得ρ＝(－R)，故选项A正确．

答案：A