
题目列表(包括答案和解析)
9.如图7所示为一弹簧振子的振动图象.求:
(1)从计时开始经过多长时间第一次达到弹性势能最大?
(2)在第2 s末到第3 s末这段时间内弹簧振子的加速度、速度、动能和弹性势能各是怎样变化的?
(3)该振子在前100 s的总位移是多少?路程是多少?
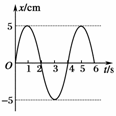
图7
解析:(1)由图知,在计时开始的时刻振子恰好以沿x轴正方向的速度通过平衡位置O,此时弹簧振子具有最大动能,随着时间的延续,速度不断减小,而位移逐渐加大,经t=T=1 s,其位移达到最大,此时弹性势能最大.
(2)由图知,在t=2 s时,振子恰好通过平衡位置,此时加速度为零,随着
时间的延续,位移值不断加大,加速度的值也变大,速度值不断变小,动能不断减小,弹性势能逐渐增大.当t=3 s时,加速度的值达到最大,速度等于零,动能等于零,弹性势能达到最大值.
(3)振子经一周期位移为零,路程为5×4 cm=20 cm,前100 s刚好经过了25个周期,所以前100 s振子位移s=0,振子路程s′=20×25 cm=500 cm=5 m.
答案:(1)1 s (2)见解析 (3)0 5 m
8.正在运转的机器,当其飞轮以角速度ω0匀速转动时,机器的振动不强烈,切断电源,飞轮的转动逐渐慢下来,在某一小段时间内机器却发生了强烈的振动,此后飞轮转速继续变慢,机器的振动也随之减弱,在机器停下来之后若重新启动机器,使飞轮转动的角速度从0较缓慢地增大到ω0,在这一过程中( ).
A.机器不一定还会发生强烈的振动
B.机器一定还会发生强烈的振动
C.若机器发生强烈振动,强烈振动可能发生在飞轮角速度为ω0时
D.若机器发生强烈振动,强烈振动时飞轮的角速度肯定不为ω0
解析:飞轮在转速逐渐减小的过程中,机器出现强烈的振动,说明发生共振现象,共振现象产生的条件是驱动力频率等于系统的固有频率,故当机器重新启动时,飞轮转速缓慢增大的过程中,一旦达到共振条件,机器一定还会发生强烈的振动.由题意可知,发生强烈共振时,飞轮的角速度一定小于ω0.
答案:BD
7.表1表示某受迫振动的振幅随驱动力频率变化的关系,若该振动系统的固有频率为f固,则( ).
表1
|
驱动力频率/Hz |
30 |
40 |
50 |
60 |
70 |
80 |
|
受迫振动振幅/cm |
10.2 |
16.8 |
27.2 |
28.1 |
16.5 |
8.3 |
A.f固=60 Hz B.60 Hz<f固<70 Hz
C.50 Hz<f固<60 Hz D.以上选项都不对
解析:由如图6所示的共振曲线可判断出f驱与f固相差越大,受迫振动的振幅越小,f驱与f固越接近,受迫振动的振幅越大,并从中看出f驱越接近f固,振幅的变化越慢.比较各组数据知f驱在50-60 Hz范围内时,振幅变化最小.因此,50 Hz<f固<60 Hz.
答案:C
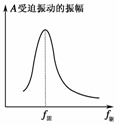
图6
6.图5所示的是弹簧振子做简谐运动的振动图象,可以判定下列说法正确的是( )

图5
A.从t1到t2时间内振子的动能不断增大,势能不断减小
B.从t2到t3时间内振幅不断增大
C.t3时刻振子处于最低点处,动能最大
D.t1,t4两时刻振子的动能、动量都相同
解析:从振动图象中可看出,从t1到t2时间内,振子的位移不断减小,所以振子的势能不断减小,由于机械能守恒,所以振子的动能不断增大,故选项A是正确的.从t2到t3时间内,振子的位移不断增大,但振幅是不变的,故选项B是错误的.t3时刻的图象在最低点,但它表示振子的位移最大,故振子的速度为0,动能为0,故选项C是错误的.t1时刻振子正向平衡位置运动,而t4时刻振子正远离平衡位置运动,虽然两时刻位移相等,势能相等,动能相等,速度大小相等,但速度方向不同,所以振子的动量不相同,故选项D也是错误的.
答案:A
5.将一个电动传感器接到计算机上,就可以测量快速变化的力,用这种方法测得的某单摆摆动时悬线上拉力的大小随时间变化的曲线如图4所示.某同学由此图象提供的信息作出的下列判断中,正确的是( )
A.t=0.2 s时摆球正经过最低点
B.t=1.1 s时摆球正经过最低点
C.摆球摆动过程中机械能减小
D.摆球摆动的周期是T=1.4 s
解析:悬线拉力在经过最低点时最大,t=0.2 s时,F有正向最大值,故A选项正确.t=1.1 s时,F有最小值,不在最低点,周期应为T=1.2 s,因振幅减小,故机械能减小,C选项正确.
答案:AC
4.心电图是现代医疗诊断的重要手段,医生从心电图上测量出相邻两波峰的时间间隔,即为心动周期,由此可以计算出1分钟内心脏跳动的次数(即心率),甲、乙两人在同一台心电图机上做出的心电图如图3所示,医生通过测量后记下甲的心率是60次/分,则由二图及甲的心率可知心电图机图纸移动的速度v以及乙的心率为( )
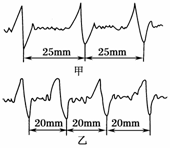
图3
A.25 mm/s 48次/分 B.25 mm/s 75次/分
C.25 mm/min 75次/分 D.25 mm/min 48次/分
解析:同一台心电图机纸带匀速移动速率相等,因此v==25 mm/s.对乙心跳周期T= s=0.8 s.心率为75次/min.
答案:B
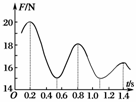
图4
3.如图2所示,两根完全相同的弹簧和一根张紧的细线将甲、乙两物块束缚在光滑水平面上,已知甲的质量大于乙的质量.当细线突然断开后,两物块都开始做简谐运动,在运动过程中( )

图2
A.甲的振幅大于乙的振幅
B.甲的振幅小于乙的振幅
C.甲的最大速度小于乙的最大速度
D.甲的最大速度大于乙的最大速度
解析:设绳的拉力大小为F,则绳断后,甲、乙的振幅为A1、A2,则kA1=kA2=F,所以A1=A2,A、B错;因甲、乙振幅相等,振动的最大能量相等,而m1>m2,故平衡位置时的速度v1<v2,C正确,D错误.
答案:C
2.(2011·北京西城模拟)如图1甲,一弹簧振子在AB间做简谐运动,O为平衡位置,如图乙是振子做简谐运动时的位移-时间图象,则关于振子的加速度随时间的变化规律,下列四个图象中正确的是( )
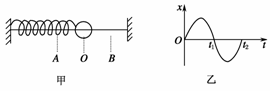
图1

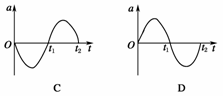
解析:设位移x=A sin t,则加速度a=-x=-sin t,当t=时a=-,故C正确.
答案:C
1.已知在单摆a完成10次全振动的时间内,单摆b完成6次全振动,两摆长之差为1.6 m.则两单摆摆长la与lb分别为( )
A.la=2.5 m,lb=0.9 m B.la=0.9 m,lb=2.5 m
C.la=2.4 m,lb=4.0 m D.la=4.0 m,lb=2.4 m
解析:由T=得==,又T=2π,所以=,且lb-la=1.6 m解得la=0.9 m,lb=2.5 m,B对.
答案:B
11.(2010·新课标全国卷)波源S1和S2振动方向相同,频率均为4Hz,分别置于均匀介质中x轴上的O、A两点处,OA=2m,如图13所示.两波源产生的简谐横波沿x轴相向传播,波速为4m/s.已知两波源振动的初始相位相同.求:
(ⅰ)简谐横波的波长;
(ⅱ)OA间合振动振幅最小的点的位置.
解析:(ⅰ)设简谐横波波长为λ,频率为ν,波速为v,则λ=①
代入已知数据得λ=1 m.②
(ⅱ)以O为坐标原点,设P为OA间的任意一点,其坐标为x,则两波源到P点的波程差Δl为Δl=x-(2-x),0≤x≤2③
其中x、Δl以m为单位.
合振动振幅最小的点的位置满足 Δl=(k+)λ,k为整数④
联立③④式,得x=0.25 m,0.75 m,1.25 m,1.75 m.⑤
答案:(ⅰ)1 m (ⅱ)0.25 m,0.75 m,1.25 m,1.75 m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com