1．已知某气体的摩尔体积为V_A，摩尔质量为M_A，阿伏加德罗常数为N_A，则根据以上数据可以估算出的物理量是　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．分子质量 　　　　　　　　B．分子体积

C．分子密度　 　　　　　　　　D．分子间平均距离

解析：根据m＝可知选项A正确；由于气体分子间距很大，故无法求出分子的体积和密度，选项B、C错误；由V＝＝d³可知选项D正确．

答案：AD

12．[解析]　设星球的半径为R，质量为M，则

(1)飞船需要的向心力由万有引力提供，则

G＝

G＝m

解得M＝.

(2)卫星在轨道上有动能和势能，其总和为E(机械能)，则G＝m₁

E＝E_k+E_p＝m₁v²+(－G)＝－G

W＝ΔE＝E₂－E₁＝G(－)．

[答案]　(1)　(2)G(－)

11．[解析]　(1)设卫星的质量为m，地球的质量为M

在地球表面附近满足G＝mg

得GM＝R²g①

卫星做圆周运动的向心力等于它受到的万有引力

m＝G②

①式代入②式，得到v₁＝.

(2)考虑①式，卫星受到的万有引力为

F＝G＝③

由牛顿第二定律F＝m(R+h)④

联立③④式解得T＝ .

[答案]　(1)v₁＝　(2)　

10．[解析]　设月球表面的重力加速度为g′，由平抛规律得

x＝v₀ ①

解得g′＝②

设近月卫星周期为T，则＝m()²R③

＝m′g′④

所以T＝2π ＝ .

[答案]　

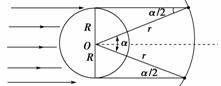
9．[解析]　由题图几何关系可得宇宙飞船绕地球作圆周运动的半径r＝R/sin，v＝rω

＝2πR/Tsin，A对；一天内飞船经历“日全食”的次数应为T₀/T，B错；由图可知，每次“日全食”过程的时间t＝＝，C错；由＝mr()²，解得：T＝ ，D对．

[答案]　AD

8．[解析]　航天飞机在飞向B处的过程中，飞机受到的引力方向和飞行方向之间的夹角是锐角，月球引力做正功；由运动的可逆性知，航天飞机在B处先减速才能由椭圆轨道进入空间站轨道；设绕月球飞行的空间站质量为m，＝mr，可以算出月球质量M；空间站的质量不知，不能算出空间站受到的月球引力大小．

[答案]　AC

7．[解析]　天体密度ρ＝＝，所以＝，故A对；万有引力近似等于重力，即G＝mg，g∝，则＝，故B错；万有引力提供向心力G＝m()²R＝m，T＝　 ，T∝ ，则＝，故C对；v＝ ，v∝ ，则＝，故D错．

[答案]　AC

6．[解析]　卫星在椭圆轨道上运行时，机械能守恒，则卫星在近地点M，运行速度大，动能大而势能小，在远地点N运行速度小，动能小，势能大，故A项错误．卫星在M点运行速度大而轨道半径小，在N点运行速度小而轨道半径大，由ω＝可知卫星在M点的角速度大于N点的角速度，B项正确．由＝ma知a_M＞a_N，故C项正确．卫星在近地点的速度大于7.9 km/s时做离心运动，到远地点N时速度一定小于7.9 km/s才能做近心运动，再回到M点，所以D错误．

[答案]　BC

5．[解析]　依题意，卫星由M到P的过程中，需要克服地球的引力做功，动能减小，而在由P到N的过程中，月球的引力对其做功，动能增大，卫星经过P点时动能最小，但不能为零，故选项A错误、B正确；物体做曲线运动时，其速度沿曲线的切线方向，故选项C正确；卫星经过P点时所受地球和月球的引力合力为零，加速度为零，故D正确．

[答案]　A

4．[解析]　人造地球卫星绕地球做匀速圆周运动的向心力为地球对卫星的万有引力．根据万有引力定律和匀速圆周运动的规律可得G＝m，v＝ ，随着轨道半径的增大，卫星的线速度减小．第一宇宙速度是卫星绕地球做匀速圆周运动的最大速度，是发射卫星的最小速度．第一宇宙速度是同步卫星运行线速度的倍，A错误，B正确；根据万有引力定律和匀速圆周运动的规律可得G＝ma，C、D错误．

[答案]　B