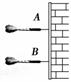
5.如图4－1－24所示，取稍长的细杆，其一端固定一枚铁钉，另一端用羽毛做

一个尾翼，做成A、B两只“飞镖”，将一软木板挂在竖直墙壁上，作为镖靶．

在离墙壁一定距离的同一处，将它们水平掷出，不计空气阻力，两只“飞镖”

插在靶上的状态如图4－1－25所示(侧视图)．则下列说法中正确的是(　) 图4－1－24

A．A镖掷出时的初速度比B镖掷出时的初速度大

B．B镖插入靶时的末速度比A镖插入靶时的末速度大

C．B镖的运动时间比A镖的运动时间长

D．A镖的质量一定比B镖的质量大

解析：由题图可知A镖的竖直位移较小，由h＝gt²可以判断A镖的运动时间较小，由于

两镖的水平位移相同，所以A镖的初速度较大，选项A、C正确．由v_y＝gt可以判断A

镖的竖直速度较小，而其水平速度较大，无法判断其合速度的大小，选项B错误．A、B

两镖的运动情况与质量无关，所以无法判断它们质量的大小，选项D错误．

答案：AC

4.2010年我国多省区发生了洪涝灾害．在某一次抗洪抢险中，我某部解放军战士在岸边，

发现河的上游有一个人蹲在一块木板上正顺流而下，解放军战士便驾驶摩托艇救人假设

江岸是平直的，洪水沿江向下游流去，各处水流速度相同均为v₁，摩托艇在静水中的航

速为v₂，保持不变．为了顺利的搭救此人，则下列做法正确的是　　　　　　　 (　)

A．摩托艇出发时，艇头要指向水中被搭救的人，且艇头指向在航行中不变

B．摩托艇出发时，艇头要指向水中被搭救的人，但在航行中需要不断改变艇头指向

C．搭救此人用的时间与水流速度有关，水流速度大时，用的时间长

D．搭救此人用的时间与水流速度无关

解析：摩托艇在水中也具有水流的速度，若以被搭救的人为参考系，摩托艇的速度为在静

水中的航速为v₂，因此航行不需要调整艇头指向，A对、B错；若知道摩托艇出发时，摩

托艇与被搭救的人的距离x，则搭救此人需用的时间t＝x/v₂，显然t与水流速度无关，故

C错、D对．

答案：AD

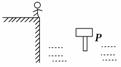
3．如图4－1－23所示，一同学在玩闯关类的游戏，他站在平台的边缘，

想在2 s内水平跳离平台后落在支撑物P上，人与P的水平距离为

3 m，人跳离平台的最大速度为6 m/s，则支撑物距离人的竖直高度　　　 图4－1－23

可能为(　)

A．1 m 　　　B．9 m 　　　C．17 m　 　　　D．20 m

解析：人以最大速度跳离平台时，用时0.5 s，下落的高度为h＝1.25 m；在2 s内，下落

的最大高度为20 m，人要跳到P上，高度差满足1.25 m≤h≤20 m，正确选项为B、C、

D.

答案：BCD

2．在无风的情况下，跳伞运动员从水平飞行的飞机上跳伞，下落过程中受到空气阻力．

下列描绘下落速度的水平分量大小v_x、竖直分量大小v_y与时间t的图象，可能正确的是

(　)

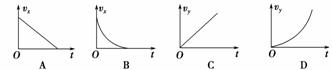
解析：降落伞在下降的过程中水平方向速度不断减小，为一变加速运动，加速度不断减

小．竖直方向先加速后匀速，在加速运动的过程中加速度不断减小，从图象上分析B图

是正确的．

答案：B

1．船在静水中的航速为v₁，水流的速度为v₂.为使船行驶到河正对岸的码头，则v₁相对v₂

的方向应为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

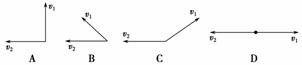
解析：为使船行驶到正对岸，v₁、v₂的合速度应指向正对岸，所以C正确．

答案：C

12. 如图2－1－33所示，为某种透明介质的截面图，△AOC为等腰直角

三角形，BC为半径R＝10 cm的四分之一圆弧，AB与水平屏幕MN垂直并接触于A点．由红光和紫光两种单色光组成的复色光射向圆心O，在AB分界面上的入射角i＝45°，结果在水平屏幕MN上出现两个亮斑．已知该介质对红光和紫光的折射率分别为n₁＝，n₂＝.

(1)判断在AM和AN两处产生亮斑的颜色；

(2)求两个亮斑间的距离．

解析：(1)设红光和紫光的临界角分别为C₁、C₂，sin C₁＝＝，C₁＝60°，同理C₂＝45°，i＝45°＝C₂，i＝45°<C₁，所以紫光在AB面发生全反射，而红光在AB面一部分折射，一部分反射，且由几何关系可知，反射光线与AC垂直，所以在AM处产生的亮斑P₁为红色，在AN处产生的亮斑P₂为红色与紫色的混合色．

(2)画出如图光路图，设折射角为r，两个光斑分别为P₁、P₂.根据折射定律

n₁＝

求得sin r＝

由几何知识可得：tan r＝，

解得AP₁＝5 cm

由几何知识可得△OAP₂为等腰直角三角形，

解得AP₂＝10 cm

所以P₁P₂＝(5+10)cm.

答案：(1)红色　红、紫的混合色　(2)(5+10)cm

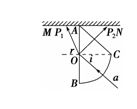
11．(1)一列简谐横波沿x轴正方向传播，在x＝0与x＝2 m的两质点振动图线分别如图

2－1－31中实线与虚线所示，由此可得出________．(填入选项前的字母)

图2－1－31

A．该波的波长可能是4 m

B．该波的周期是5 s

C．波的传播速度可能是2 m/s

D．在t＝2 s时刻，x＝2 m处的质点正向上运动

(2)如图2－1－32所示，AOB是由某种透明物质制成的圆柱体横截面(O为

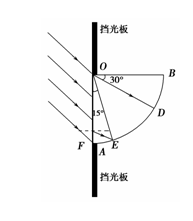圆心)，折射率为.今有一束平行光以45°的入射角射向圆柱体的OA平面，这些光线中有一部分不能从柱体的AB面上射出，设射到OB面的光线全部被吸收，不考虑OA面的反射，求在圆柱AB面上能射出光线的部分占AB表面的比例．

解析： (2)光路图如右图所示：

n＝　　　　　　　　　　　　　　　　　　　 ①

sin r＝＝

∴r＝30°，∠BOD＝30°　　　　　　　　　　　　 ②

即从O点射入的光线射到D点，BD之间无光线射出．

设该透明物质的临界角为C，则

sin C＝，解得∠C＝45°　　　　　　　　　　　 ③

设从F点入射到E点的光线在AB面发生全反射．

由几何关系可知，∠FOE＝15°　　　　　　　　　　 ④

即从AE点之间的光线发生全反射．

圆柱AB面上能射出光线的部分占AB表面＝⑤

位置如图中DE部分．　　　　　　　　　　　　　　 ⑥

答案：(1)C　(2)

10.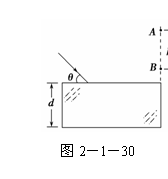　 如图2－1－30所示，真空中有一下表面镀反射膜的平行玻璃砖，其折射

率n＝，一束单色光与界面成θ＝45°角斜射到玻璃砖表面上，最后在玻璃砖的右侧面竖直光屏上出现两个光点A和B，A和B相距h＝2.0 cm.已知光在真空中的传播速度c＝3.0×10⁸ m/s.试求：

(1)该单色光在玻璃砖中的传播速度；

(2)该单色光射入到玻璃砖的折射角；

(3)玻璃砖的厚度d.

解析：(1)由折射率公式n＝

解得：v＝＝×10⁸ m/s.

(2)由折射率公式n＝

解得：sin θ₂＝＝，θ₂＝30°.

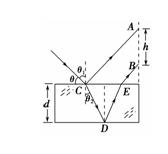(3)作出如右图所示的光路，△CDE为等边三角形，四边形ABEC为梯形，

CE＝AB＝h.玻璃的厚度d就是边长为h的等边三角形的高，故：d＝h·cos 　

30°＝h＝1.732 cm.

答案：(1)×10⁸ m/s　(2)30°　(3)1.732 cm

9.　 (1)一足够大的水池内盛有某种透明液体，液体的深度为H，在水池的底部

放一点光源S，其中一条光线以30°入射角射到液体与空气的界面上，它的反射光线与折射光线的夹角为105°，如图2－1－29所示．求：

①液体的折射率；

②液体表面亮斑的面积．

(2)光是一种电磁波，当光从水中射入空气中时，波长会________(填写“变长”，“变短”、“不变”)，如果光的频率为6.7×10¹⁴ Hz，空气中光速约为3.0×10⁸ m/s，则在空气中的波长为________m.

解析：(1)①由图知入射角i＝30°，折射角r＝45°，n＝＝＝1.414.

②若发生全反射，入射角C应满足sin C＝，C＝45°

亮斑半径R＝Htan C＝H，亮斑面积S＝πH².

(2)变长　由C＝λf得λ＝＝ m＝4.5×10^－7 m.

答案：(1)①1.414　②πH²　(2)变长　4.5×10^－7 m

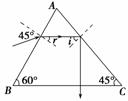
8.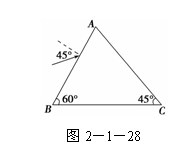　 (2011·海南海口模拟)一束光波以45°的入射角，从AB面射入如图

2－1－28所示的透明三棱镜中，棱镜折射率n＝.试求光进入AB面的折射角，并在图上画出该光束在棱镜中的光路．

解析：sin r＝＝＝，r＝30°

由sin C＝＝，得C＝45°.

光在AC面发生全反射，并垂直BC面射出．

答案：C＝45°　光路图如下