
题目列表(包括答案和解析)
8.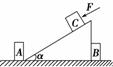 如图2-2-29所示,一倾角为α的斜面体置于固定在光滑水平地面
如图2-2-29所示,一倾角为α的斜面体置于固定在光滑水平地面
上的物体A、B之间,斜面体恰好与物体A、B接触.一质量为m的
物体C恰能沿斜面匀速下滑,此时斜面体与A、B均无作用力.
若用平行于斜面的力F沿斜面向下推物体C,使其加速下滑,则下 图2-2-29
列关于斜面体与物体A、B间的作用力的说法正确的是 ( )
A.对物体A、B均无作用力
B.对物体A有向左的压力,大小为Fcos α
C.对物体B有向右的压力,大小为mgcos αsin α
D.对物体A有向左的压力,大小为mgcos αsin α
解析:本题考查受力分析、力的平衡问题.物体C恰能沿斜面匀速下滑,则C与斜面间
的滑动摩擦力Ff=mgsin α,用力F推物体C使其加速运动,C与斜面间的滑动摩擦力不
变;以斜面为研究对象,C对斜面的压力在水平方向向右的分力为F1=mgcos αsin α,
C对斜面的摩擦力在水平方向向左的分力为F2=mgsin αcos α,则F1=F2,说明斜面与地
面间无摩擦力,斜面相对地面没有运动趋势,斜面对物体A、B均无作用力.本题难度易.
答案:A
7.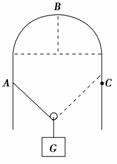 在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁
在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁
的地域风情和人文特色.如图2-2-28所示,在竖直放置的穹形
光滑支架上,一根不可伸长的轻绳通过轻质滑轮悬挂一重物G.现
将轻绳的一端固定于支架上的A点,另一端从B点沿支架缓慢地向
C点靠近(C点与A点等高).则绳中拉力大小变化的情况是 ( )
A.先变小后变大 B.先变小后不变
C.先变大后不变 D.先变大后变小 图2-2-28
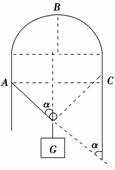 解析:由于轻绳中各处的张力相等,若两悬挂点之间的水平距离为
解析:由于轻绳中各处的张力相等,若两悬挂点之间的水平距离为
d,绳长为l,如图所示,则sin α=,cos α=.由平衡条件可
得,2Fcos α=G,所以绳中的拉力F=,故随着两悬挂点水
平距离d的增大,拉力增大;当两悬挂点水平距离d不变后,拉力
也不变,所以C正确.
答案:C
6.如图2-2-27(甲)所示,一物块在粗糙斜面上,在平行斜面向上的外力F作用下,斜面
和物块始终处于静止状态,当F按图2-2-27(乙)所示规律变化时,关于物块与斜面间
摩擦力的大小变化的说法中正确的是 ( )
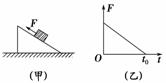
图2-2-27
A.一定增大 B.可能一直减小
C.可能先减小后增大 D.可能一直增大
答案:CD
5. (2011·青岛检测)如图2-2-26所示,质量为m的两木块a和b叠放
(2011·青岛检测)如图2-2-26所示,质量为m的两木块a和b叠放
在水平面上,a受到斜向上与水平方向成θ角的力的作用,b受到斜
向下与水平方向成θ角的力的作用,两力大小均为F,两木块均保持
静止状态,则 ( ) 图2-2-26
A.a、b之间一定存在静摩擦力
B.b与地面之间一定存在静摩擦力
C.b对a的支持力一定小于mg
D.地面对b的支持力一定小于2mg
答案:AC
4.如图2-2-25所示,物体m静止于倾角为θ的斜面上,现用垂直于
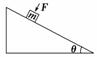 斜面的压力F=kt(k为比例常量,t为时间)作用在物体上.从t=0开
斜面的压力F=kt(k为比例常量,t为时间)作用在物体上.从t=0开
始,物体所受摩擦力Ff随时间t的变化关系是下图中的 ( ) 图2-2-25
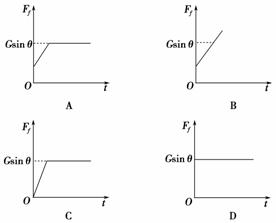
解析:未加压力F之前,物体处于静止状态,由平衡条件可得:Ff=Gsin θ,当加上压力
F后,物体仍处于静止状态,因此Ff仍为Gsin θ,故D正确.
答案:D
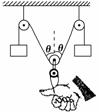
3.如图2-2-24所示是某同学对颈椎病人设计的一个牵引装置的示意图,
一根绳绕过两个定滑轮和一个动滑轮后两端各挂着一个相同的重物,与
动滑轮相连的帆布带拉着病人的颈椎(图中是用手指代替颈椎做实验),
整个装置在同一竖直平面内.如果要增大手指所受的拉力,可采取的办
法是 ( ) 图2-2-24
A.只增加与重物相连细绳的长度
B.只增加重物的重量
C.只将手指向下移动
D.只将手指向上移动
解析:手指所受的拉力等于2mgcos θ,增加重物重量,减小夹角θ,都可以使拉力增大,
选项B、C正确.
答案:BC
2.如图2-2-23所示,一运送救灾物资的直升飞机沿水平方向匀速飞行.
已知物资的总质量为m,吊运物资的悬索与竖直方向成θ角.设物资
所受的空气阻力为Ff,悬索对物资的拉力为F,重力加速度为g,
则 ( ) 图2-2-23
A.Ff=mgsin θ B.Ff=mgtan θ
C.F=mgcos θ D.F=
解析:救灾物资匀速飞行,受力平衡,它受到向下的重力mg,向右的阻力Ff和沿细绳斜
向上的拉力,可得Ff=mgtan θ,B项正确.
 答案:B
答案:B
1.两个大小分别为F1和F2(F2<F1)的力作用在同一质点上,它们的合力
的大小F满足 ( )
A.F1≤F≤F2 B.≤F≤
C.F1-F2≤F≤F1+F2 D.F-F≤F2≤F+F
解析:共点的两个力合成,同向时最大为F1+F2,反向时最小为F1-F2.
 答案:C
答案:C
12.如图9-2-28所示,平行金属导轨竖直放置,导轨间距为L=1 m,上端接有电阻R1
=3Ω,下端接有电阻R2=6 Ω,虚线OO′下方是垂直于导轨平面的匀强磁场.现将
质量m=0.1 kg、电阻不计的金属杆ab,从OO′上方某处垂直导轨由静止释放,杆下
落0.2 m过程中始终与导轨保持良好接触,加速度a与下落距离h的关系图象如图9
-2-29所示.求:

图9-2-28 图9-2-29
(1)磁感应强度B;
(2)杆下落0.2 m过程中通过电阻R2的电荷量q.
解析:(1)由图象知,杆自由下落距离是0.05 m,当地重力加速度g=10 m/s2,
则杆进入磁场时的速度v==1 m/s ①
由图象知,杆进入磁场时加速度a=-g=-10 m/s2 ②
由牛顿第二定律得mg-F安=ma ③
回路中的电动势E=BLv ④
杆中的电流I= ⑤
R并= ⑥
F安=BIL= ⑦
解得B= =2 T ⑧
(2)杆在磁场中运动产生的平均感应电动势= ⑨
杆中的平均电流= ⑩
通过杆的电荷量Q=·Δt ⑪
通过R2的电荷量q=Q=0.05 C ⑫
答案:(1)2 T (2)0.05 C
11. 如图9-2-27所示,两根平行金属导轨固定在同一水平面
如图9-2-27所示,两根平行金属导轨固定在同一水平面
内,间距为l,导轨左端连接一个电阻R.一根质量为m、电阻
为r的金属杆ab垂直放置在导轨上.在杆的右方距杆为d处
有一个匀强磁场,磁场方向垂直于轨道平面向下,磁感应强
度为B.对杆施加一个大小为F、方向平行于导轨的恒力,使
杆从静止开始运动,已知杆到达磁场区域时速度为v,之后
进入磁场恰好做匀速运动.不计导轨的电阻,假定导轨与杆之间存在恒定的阻力.求:
(1)导轨对杆ab的阻力大小f;
(2)杆ab中通过的电流及其方向;
(3)导轨左端所接电阻R的阻值.
解析:(1)杆进入磁场前做匀加速运动,有
F-f=ma ①
v2=2ad ②
解得导轨对杆的阻力f=F-. ③
(2)杆进入磁场后做匀速运动,有F=f+FA ④
杆ab所受的安培力
FA=IBl ⑤
解得杆ab中通过的电流I= ⑥
杆中的电流方向自a流向b ⑦
(3)杆ab产生的感应电动势E=Blv ⑧
杆中的感应电流I= ⑨
解得导轨左端所接电阻阻值R=-r ⑩
答案:(1)F- (2),方向自a流向b
(3)-r
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com