
题目列表(包括答案和解析)
8.三个同样的电阻,额定功率均为10 W,把其中两个并联再与第三个串联接入电路,则
此电路允许消耗的最大电功率为 ( )
A.10 W B.15 W C.20 W D.30 W
解析:设每个电阻的阻值为R,额定电流为I,由P=I2R=10 W,电路消耗的最大电功
率为P总=I2=×I2R=15 W.
答案:B
7.(2011·济南模拟)一台国产封闭型贮水式电热水器的铭牌上所列的主要技术参数如表所
示.根据表中所提供的数据,计算出此电热水器在额定电压下处于加热状态时,通过电
热水器的电流约为 ( )
|
额定容量 |
54 L |
最高水温 |
75℃ |
|
额定功率 |
1 500 W |
额定压力 |
0.7 MPa |
|
额定电压 |
220 V |
电器类别 |
Ⅰ类 |
A.6.8 A B.0.15 A C.4.4 A D.0.23 A
解析:由P=UI,可知该电热水器在额定电压下处于加热状态时的电流为:I==
A≈6.8 A,故选项A正确.
答案:A
6.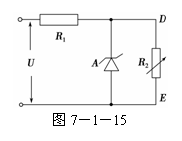 如图7-1-15所示,A为一稳压管,它的作用是保证DE
如图7-1-15所示,A为一稳压管,它的作用是保证DE
两端的电压UDE恒定不变,当流过稳压管的电流在5 mA
和40 mA之间时,UDE就稳定在10 V,R2为一可变电阻,
它的最小值为500 Ω,最大值为无穷大(即断路).设电源
电压U=20 V,则当R2变化时,为使UDE稳定在10 V,
R1可取下列几个电阻值中的 ( )
A.100 Ω B.200 Ω C.300 Ω D.4 000 Ω
解析:R1两端的电压为10 V,干路中最大的电流为40
mA,解得R1=250 Ω,干路中最小的电流为5 mA+20 mA=25 mA,解得R1=400 Ω,
所以250 Ω<R1<400 Ω,C项符合.
答案:C
5.有一横截面积为S的铜导线,流经其中的电流为I,设每单位体积的导线中有n个自由
电子,电子的电荷量为q.此时电子的定向移动速度为v,在Δt时间内,通过导线横截面
的自由电子数目可表示为 ( )
A.nvS B.nvΔt C. D.
解析:根据电流的定义式可知,在Δt内通过导线横截面的电荷量Q=IΔt
所以在这段时间内通过的自由电子数为N==
所以C项正确,D项错.
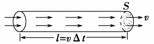 由于自由电子定向移动的速率是v,因此在时间Δt内,位于
由于自由电子定向移动的速率是v,因此在时间Δt内,位于
以横截面S为底、长l=vΔt的这段导线内的自由电子都能通
过横截面(如图).这段导线的体积V=Sl=SvΔt,所以Δt内通
过横截面S的自由电子数为N=nV=nSvΔt.选项A、B均错.
答案:C
4.一白炽灯泡的额定功率与额定电压分别为36 W与36 V.若把此灯泡接到输出电压为18
V的电源两端,则灯泡消耗的电功率 ( )
A.等于36 W B.小于36 W,大于9 W
C.等于9 W D.小于36 W
解析:白炽灯正常工作时的电阻R额==36 Ω,当加上18 V电压时,P实=>=
W=9 W,故选项B对.
答案:B
3.0 C
答案:ABD
3.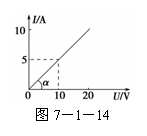 (2011·杭州模拟)如图7-1-14所示是某导体的I-U图线,图
(2011·杭州模拟)如图7-1-14所示是某导体的I-U图线,图
中α=45°,下列说法正确的是 ( )
A.通过电阻的电流与其两端的电压成正比
B.此导体的电阻R=2 Ω
C.I-U图线的斜率表示电阻的倒数,所以R=cot 45°=1.0 Ω
D.在R两端加6.0 V电压时,每秒通过电阻截面的电荷量是
2.下列说法中正确的是 ( )
A.由R=可知,导体的电阻跟导体两端的电压成正比,跟导体中的电流成反比
B.由I=可知,通过导体的电流跟导体两端的电压成正比,跟它的电阻成反比
C.导体的电阻率由导体本身的物理条件决定,与温度无关
D.欧姆定律I=,不仅适用于纯电阻电路,对于非纯电阻电路也适用
答案:B
1.下列关于电流方向的说法中,正确的是 ( )
A.电流的方向就是自由电子定向移动的方向
B.电流的方向规定为正电荷定向移动的方向
C.在金属导体中,电流的方向与自由电子定向移动的方向相反
D.在电解液中,电流的方向与离子定向移动的方向相同
解析:电流方向规定为与正电荷定向移动的方向相同,与负电荷移动的方向相反,在电
解液中电流方向与正离子定向移动的方向相同.
答案:BC
12.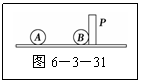 两个带电小球A和B,质量分别为m1、m2,带有同种
两个带电小球A和B,质量分别为m1、m2,带有同种
电荷,带电荷量分别为q1、q2.A、B两球均放在光滑绝
缘的水平板上,A球固定,B球被质量为m3的绝缘挡
板P挡住静止,A、B两球相距为d,如图6-3-31所
示.某时刻起挡板P在向右的水平力F作用下开始向右做匀加速直线运动,加速度大
小为a,经过一段时间带电小球B与挡板P分离,在此过程中力F对挡板做功W.求:
(1)力F的最大值和最小值?
(2)带电小球B与挡板分离时的速度?
(3)从开始运动到带电小球与挡板P分离的过程中,电场力对带电小球B做的功?
解析:(1)开始运动时力F最小,以B球和挡板为研究对象,由牛顿第二定律得:
F1+k=(m3+m2)a
解得最小力为:F1=(m3+m2)a-k
B球与挡板分离后力F最大,以挡板为研究对象,由牛顿第二定律解得最大力为:F2
=m3a.
(2)B球与挡板分离时,以B球为研究对象,由牛顿第二定律得:k=m2a ①
B球匀加速直线运动的位移为:s=r-d ②
由运动学公式得:v2=2as ③
由①②③联立解得,带电小球B与挡板分离时的速度为:
v= .
(3)设B球对挡板做功W1,挡板对B球做功W2,电场力对B球做功W3,在B球与挡板
共同运动的过程中,对挡板应用动能定理得:W+W1=m3v2 ④
挡板对B球做的功W2=-W1 ⑤
对B球应用动能定理得:W3+W2=m2v2 ⑥
由④⑤⑥联立解得电场力对B球做功为:
W3=(m2+m3)a-W.
答案:(1)m3a (m3+m2)a-
(2)
(3)(m2+m3)a-W
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com