10．总质量为80 kg的跳伞运动员从离地500 m的直升机上跳下，经过2 s拉开绳索开启降落伞．如图所示是跳伞过程中的v­t图象，试根据图象(g取10 m/s²)，求

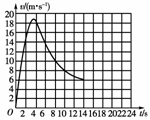
(1)t＝1 s时运动员的加速度和所受阻力的大小；

(2)估算14 s内运动员下落的高度及克服阻力做的功；

(3)估算运动员从飞机上跳下到着地的总时间．

答案：(1)8 m/s²　160 N　(2)158 m　1.25×10⁵ J　(3)71 s

解析：(1)从图中可以看出，在t＝2 s内运动员做匀加速运动，其加速度大小为a＝＝ m/s²＝8 m/s²

设此过程中运动员受到的阻力大小为F_f，根据牛顿第二定律，有mg－F_f＝ma

得F_f＝m(g－a)＝80×(10－8)N＝160 N.

(2)从图中由面积估算得出运动员在14 s内下落了h＝39.5×2×2 m＝158 m

根据动能定理，有mgh－W_f＝mv²

所以有W_f＝mgh－mv²＝J≈1.25×10⁵ J.

(3)14 s后运动员做匀速运动的时间为t′＝＝ s＝57 s

运动员从飞机上跳下到着地需要的总时间

t_总＝t+t′＝(14+57)s＝71 s.

9．如图所示，小球沿倾角α＝30°的粗糙斜面的顶端B由静止开始滑下，与置于斜面底端A处的木板碰撞后反向弹回，假设每次与板碰撞后都能弹回本次下滑距离的，空气阻力不计，小球与木板碰撞后无动能损失，且A、B间距离x₀＝6 m，求小球在静止前所通过的总路程为多少．

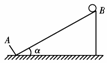
答案：30 m

解析：由题意可知，小球先沿斜面向下加速运动，与挡板碰后沿斜面向上减速上升，依此反复，由于不断地克服摩擦力做功，每次与挡板A相碰后，速度都比前一次要小，故最终停于挡板前．

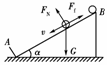
设小球与斜面间的动摩擦因数为μ，球沿斜面下滑过程受力分析如图所示．

研究小球第一次由静止从距A端x₀处的B点下滑和碰撞弹回上升到速度为零的全过程，由动能定理得：mgsin α－μmgcos α＝0，∴ μ＝tan α.

小球最终一定停在A处，研究球从B处静止下滑到最终停在A处的全过程，由动能定理得：mgx₀sin α－μmgx_总cos α＝0，所以小球通过的总路程为：x_总＝＝5x₀＝30 m.

8．如图所示，质量为m的小物块A放在质量为M的木板B的左端，B在水平拉力的作用下沿水平地面匀速向右滑动，且A、B相对静止．某时刻撤去水平拉力，经一段时间，B在地上滑行了一段距离x，A在B上向右滑行了一段距离L，最后A和B都停下，A、B间的动摩擦因数为 μ₁，B与地面间的动摩擦因数为μ₂，且μ₂>μ₁，求x的表达式．

答案：

解析：如图所示，设匀速运动时速度为v.

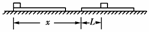
撤去外力之后至停止，A在水平方向受力F＝μ₁mg，动能定理－F(L+x)＝0－mv²，B在水平方向受力F＝μ₁mg，F_地＝μ₂(m+M)g，动能定理－F_地x+Fx＝0－Mv²，解得x＝.

7．(2010·龙岩模拟)光滑斜面上有一个小球自高为h的A处由静止开始滚下，到达光滑水平面上B点时的速率为v₀.光滑水平面上每隔相等的距离设置了一个与小球运动方向垂直的阻挡条，如图所示，小球越过n条阻挡条后停下来．若让小球从h高处以初速度v₀滚下，则小球能越过阻挡条的条数为(设小球每次越过阻挡条时损失的动能相等，假设水平面光滑)(　)

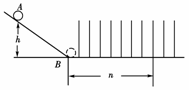
A．n　 　　　　　　　　　　　　　　　　　　　 B．2n

C．3n　 　　　　　　　　　　　　　　　　　　 D．4n

答案：B

解析：对于第一次，根据动能定理可得：mv₀²＝nΔE_k，mv₀²＝mgh对于第二次，根据动能定理可知：mv₀²+mgh＝NΔE_k，N＝2n.

6．(2009·上海单科)小球由地面竖直上抛，上升的最大高度为H，设所受阻力大小恒定，地面为零势能面．在上升至离地高度h处，小球的动能是势能的两倍，在下落至离地高度h处，小球的势能是动能的两倍，则h等于(　)

A．H/9　 　　　　　　　　　　　　　　　　　 B．2H/9

C．3H/9　 　　　　　　　　　　　　　　　　 D．4H/9

答案：D

解析：小球上升至最高点过程：－mgH－F_阻H＝0－mv₀²；小球上升至离地高度h处过程：－mgh－F_阻h＝mv₁²－mv₀²，又mv₁²＝2mgh；小球上升至最高点又下降至离地高度h处过程：－mgh－F_阻(2H－h)＝mv₂²－mv₀²，又mv₂²＝mgh；以上各式联立解得h＝H，选项D正确．

5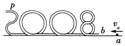．某兴趣小组设计了如图所示的玩具轨道，其中“2008”四个等高数字用内壁光滑的薄壁细圆管弯成，固定在竖直平面内(所有数字均由圆或半圆组成，圆半径比细管的内径大得多)，底端与水平地面相切．弹射装置将一个小物体(可视为质点)以v_a＝5 m/s的水平初速度由a点弹出，从b点进入轨道，依次经过“8002”后从p点水平抛出．小物体与地面ab段间的动摩擦因数μ＝0.3，不计其他机械能损失．已知ab段长L＝1.5 m，数字“0”的半径R＝0.2 m，小物体质量m＝0.01 kg，g＝10 m/s².求：

(1)小物体从p点抛出后的水平射程．

(2)小物体经过数字“0”的最高点时管道对小物体作用力的大小和方向．

答案：(1)0.8 m　(2)0.3 N　方向竖直向下

解析：(1)设小物体运动到p点时的速度大小为v，对小物体由a运动到p过程应用动能定理得－μmgL－2Rmg＝mv²－mv_a²，小物体自p点做平抛运动，设运动时间为t，水平射程为x，则2R＝gt²，x＝vt.联立以上各式，代入数据解得x＝0.8 m.

(2)设在数字“0”的最高点时管道对小物体的作用力大小为F，取竖直向下为正方向，则F+mg＝

代入数据解得F＝0.3 N，方向竖直向下．

4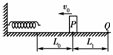．一轻弹簧左端固定在墙壁上，右端自由，一质量为m的滑块从距弹簧右端L₀的P点以初速度v₀正对弹簧运动，如图所示，滑块与水平面的动摩擦因数为μ，在与弹簧碰后又反弹回来，最终停在距P点为L₁的Q点，求：在滑块与弹簧的碰撞过程中弹簧的最大压缩量为多少？

答案：－－L₀

解析：对滑块来回过程利用动能定理列式求解．设弹簧最大压缩量为x，在滑块向左运动的过程中，由动能定理可得：

－μmg(x+L₀)－W_弹＝0－mv₀²①

在滑块返回的过程中，由动能定理得：

W_弹－μmg(x+L₀+L₁)＝0②

由①②得：x＝－－L₀.

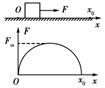
3．静置于光滑水平面上坐标原点处的小物块，在水平拉力F作用下沿x轴方向运动，拉力F随物块所在位置坐标x的变化关系如图所示，图线为半圆．则小物块运动到x₀处时的动能为(　)

A．0　 　　　　　　　　　　　　　　　　　　　 B.F_mx₀

C.F_mx₀　 　　　　　　　　　　　　　　　　　 D.x₀²

答案：C

解析：根据动能定理可知，F做的功为F­x图象所包围的面积，即W＝F_mx₀.C选项正确．

2．(2010·黄冈模拟)我国自行研制的ZTZ­99式主战坦克，抗弹能力、火力性能等综合性能都占世界领先地位，该坦克的质量为m，若在平直的公路上从静止开始加速，前进较短的距离s速度便可达到最大值v_m.设在加速过程中发动机的功率恒为P，坦克所受阻力恒为f，当速度为v(v_m>v)时，所受牵引力为F.对坦克在这段位移内的有关物理量，以下说法正确的是(　)

A．坦克的牵引力做功为Fs

B．坦克的牵引力做功为mv_m²+fs

C．坦克的牵引力做功为mv_m²

D．坦克的最大速度v_m＝

答案：BD

解析：发动机的功率恒为P，则牵引力是变力，不能用Fs求功，A错；由动能定理得W－fs＝mv_m²，可知B正确、C错；最大速度时F_牵＝f，由P＝F_牵v_m，可知D正确．

1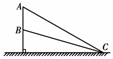．如图所示，质量相同的物体分别自斜面AC和BC的顶端由静止开始下滑，物体与斜面间的动摩擦因数都相同，物体滑至斜面底部C点时的动能分别为Ek₁和Ek₂，下滑过程中克服摩擦力所做的功分别为W₁和W₂，则(　)

A．Ek₁>Ek₂，W₁<W₂　 　　　　　　　　　　 B．Ek₁>Ek₂，W₁＝W₂

C．Ek₁＝Ek₂，W₁>W₂　 　　　　　　 D．Ek₁<Ek₂，W₁>W₂

答案：B

解析：设斜面的倾角为θ，则下滑过程中克服摩擦力做的功为W＝μmglcos θ＝μmgl_水平，所以两种情况下克服摩擦力做的功相等，再由于B的高度比A低所以Ek₁>Ek₂，选B.