8．皮带传送机传送矿石的速度v大小恒定，在轮缘A处矿石和皮带恰好分离，如图所示．若轮子的半径为R，则通过A点的半径OA和竖直方向OB的夹角θ为(　)

A．arcsin 　 　　　　　　　　　　　　　 B．arccot

C．arctan 　 　　　　　　　　　　　　　 D．arccos

答案：D

解析：矿石和皮带分离时两者之间的弹力为零，将重力沿半径OA方向和垂直于OA的方向分解，有mgcos θ＝m，则θ＝arccos ，D正确．

7．如图所示为某一皮带传动装置．主动轮的半径为r₁，从动轮的半径为r₂.已知主动轮做顺时针转动，转速为n，转动过程中皮带不打滑．下列说法正确的是(　)

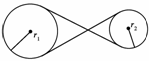
A．从动轮做顺时针转动

B．从动轮做逆时针转动

C．从动轮的转速为n

D．从动轮的转速为n

答案：BC

解析：因为主动轮顺时针转动，从动轮通过皮带的摩擦力带动转动，所以从动轮逆时针转动，A错误，B正确；由于通过皮带传动，皮带与轮边缘接触处的速度相等，所以由2πnr₁＝2πn₂r₂，得从动轮的转速为n₂＝，C正确，D错误．

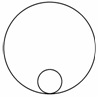
6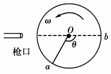．(2010·泰安模拟)如图所示，直径为d的纸制圆筒以角速度ω绕垂直纸面的轴O匀速转动(图示为截面)．从枪口发射的子弹沿直径穿过圆筒．若子弹在圆筒旋转不到半周时，在圆周上留下a、b两个弹孔，已知aO与bO夹角为θ，求子弹的速度．

答案：

解析：子弹射出后沿直线运动，从a点射入，从b点射出，该过程中圆筒转过的角度为π－θ.

设子弹速度为v，则子弹穿过筒的时间t＝

此时间内筒转过的角度α＝π－θ

据α＝ωt得，π－θ＝ω

则子弹速度v＝

5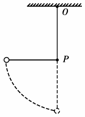．(2010·长沙模拟)质量为m的小球，用长为l的细线悬挂在O点，在O点的正下方处有一光滑的钉子P，把小球拉到与钉子P等高的位置，摆线被钉子挡住．如图让小球从静止释放，当小球第一次经过最低点时(　)

A．小球运动的线速度突然减小

B．小球的角速度突然减小

C．小球的向心加速度突然减小

D．悬线的拉力突然增大

答案：BC

解析：小球第一次经过最低点时，线速度大小不变，A错误．由ω＝，r突然变大，ω突然减小，B正确．由a_向＝，r突然变大，a_向突然减小，C正确，悬线拉力F＝mg+m＝mg+ma_向应突然减小，D错误．

4．如图所示，一只小球在固定的竖直平面内的圆环内侧连续做圆周运动，当它第4次经过最低点时速率为7 m/s，第5次经过最低点时速率为5 m/s，那么当它第6次经过最低点时速率应该为(在所研究的过程中小球始终没有脱离圆周轨道)(　)

A．一定是3 m/s　 　　　　　　　　　　　　　　 B．一定是1 m/s

C．一定大于1 m/s　 　　　　　　　　 D．一定小于1 m/s

答案：C

解析：因为圆周运动的速度减小，所以N减小，所以f减小．

故Ek₄－Ek₅>Ek₅－Ek₆.

即49－25>25－Ek₆.

解得v₆>1 m/s

3．如图所示，甲、乙、丙三个轮子依靠摩擦传动，相互之间不打滑，其半径分别为r₁、r₂、r₃.若甲轮的角速度为ω₁，则丙轮的角速度为(　)

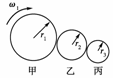
A.　 　　　　　　　　　　　　　　　　　　 B.　

C.　 　　　　　　　　　　　　　　　　　　 D.

答案：A

解析：对甲轮边缘的线速度v₁＝r₁ω₁

对乙轮边缘的线速度v₂＝r₂ω₂

对丙轮边缘的线速度v₃＝r₃ω₃

由各轮边缘的线速度相等得：r₁ω₁＝r₂ω₂＝r₃ω₃

所以ω₃＝，A选项正确．

2．游客乘坐过山车，在圆弧轨道最低点处获得的向心加速度达到20 m/s²，g取10 m/s²，那么此位置座椅对游客的作用力相当于游客重力的(　)

A．1倍　　　　　　　　　　　　　　　 B．2倍　　

C．3倍　　　　　　　　　　　　　　　 D．4倍

答案：C

解析：游客的重力mg和座椅对游客的支持力F_N的合力来提供游客做圆周运动的向心力，由牛顿第二定律F_N－mg＝ma，即F_N＝mg+ma＝3mg.

1．一只小狗拉着雪橇在水平冰面上沿着圆弧形的道路匀速行驶，如图为雪橇受到的牵引力F及摩擦力F₁的示意图(O为圆心)，其中正确的是(　)

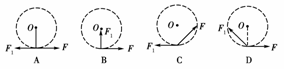
答案：C

解析：雪橇做匀速圆周运动，牵引力F及摩擦力F₁的合力提供向心力，指向圆心，A、B项错误；滑动摩擦力F₁是阻力，与线速度反向，D项错误．

20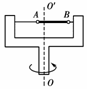．(12分)如图所示的水平转盘可绕竖直轴OO′旋转，盘上水平杆上穿着两个质量均为m的小球A和B.现将A和B分别置于距轴r和2r处，并用不可伸长的轻绳相连．已知两球与杆之间的最大静摩擦力都是f_m.试分析转速ω从零逐渐增大，两球对轴保持相对静止过程中，在满足下列条件下，ω与m、r、f_m的关系式．

(1)绳中出现张力时；

(2)A球所受的摩擦力改变方向时；

(3)两球对轴刚要滑动时．

答案：(1)ω₁＝　(2)ω₂＝　(3)ω₃＝

解析：(1)由于ω从零开始逐渐增大，当ω较小时，A和B只靠自身静摩擦力提供向心力．

A球：mω²r＝f_A；B球：mω²·2r＝f_B.

随ω增大，静摩擦力不断增大，直至ω＝ω₁时，将有f_B＝f_m，即mω₁²·2r＝f_m，则ω₁＝.

即ω从ω₁开始继续增加，绳上将出现张力T.

(2)当绳上出现张力后，对B球有mω²·2r＝f_m+T，并且ω增加时，绳上张力将增加．对于A球应有mω²r＝f_A+T，可知随ω的增大，A球所受摩擦力将不断减小，直至f_A＝0时，角速度ω＝ω₂.

此时，A球mω₂²r＝T；B球mω₂²·2r＝f_m+T，

解之得ω₂＝.

(3)当角速度从ω₂继续增加时，A球所受的摩擦力方向将沿杆指向外侧，并随ω的增大而增大，直至f_A＝f_m为止．设此时角速度为ω₃，并有如下情况：

A球mω₃²r＝T－f_m，B球mω₃²·2r＝f_m+T.

解之得ω₃＝.

若角速度从ω₃继续增加，A和B将一起向B一侧甩出．

19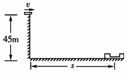．(2010·厦门模拟)(10分)我国射击运动员曾多次在国际大赛中为国争光，在2008年北京奥运会上又夺得射击冠军．我们以打靶游戏来了解射击运动．某人在塔顶进行打靶游戏，如图所示，已知塔高H＝45 m，在与塔底部水平距离为s处有一电子抛靶装置，圆形靶可被竖直向上抛出，初速度为v₁，且大小可以调节．当该人看见靶被抛出时立即射击，子弹以v₂＝100 m/s的速度水平飞出．不计人的反应时间及子弹在枪膛中的运动时间，且忽略空气阻力及靶的大小(取g＝10 m/s²)．

(1)当s的取值在什么范围时，无论v₁多大都不能被击中？

(2)若s＝200 m，v₁＝15 m/s时，试通过计算说明靶能否被击中？

答案：(1)s>300 m　(2)不能

解析：(1)欲使靶不被击中，抛靶装置应在子弹射程范围外．

由H＝gt²，s＝v₂t代入数据得s＝300 m；故s的取值范围应为s>300 m.

(2)设经过时间t₁，子弹恰好在抛靶装置正上方，此时靶离地面h₁，子弹下降了h₂，

h₁＝v₁t₁－gt₁²，h₂＝gt₁²，s＝v₂t₁，

联立以上各式解得h₁＝10 m，h₂＝20 m.

所以h₁+h₂≠H，靶不能被击中．