2．(2010·江门模拟)跳伞表演是人们普遍喜欢的观赏性体育项目，当运动员从直升飞机由静止跳下后，在下落过程中不免会受到水平风力的影响，下列说法中正确的是(　)

A．风力越大，运动员下落时间越长，运动员可完成更多的动作

B．风力越大，运动员着地速度越大，有可能对运动员造成伤害

C．运动员下落时间与风力无关

D．运动员着地速度与风力无关

答案：BC

解析：运动员下落过程中，下落时间仅与竖直方向的运动有关，与水平方向的运动无关，即A错，C正确．着地速度是竖直方向速度与风速的合成．即B正确．D错．

1．关于物体做曲线运动，下列说法正确的是(　)

A．物体在恒力作用下不可能做曲线运动

B．物体在变力作用下有可能做曲线运动

C．做曲线运动的物体，其速度方向与加速度方向不在同一条直线上

D．物体在变力作用下不可能做直线运动

答案：BC

解析：平抛运动是物体在恒力作用下的曲线运动，匀速圆周运动是物体在变力作用下的曲线运动．

13．(2010·福建理综)火星探测项目是我国继神舟载人航天工程、嫦娥探月工程之后又一个重大太空探索项目．假设火星探测器在火星表面附近圆形轨道运行的周期为T₁，神舟飞船在地球表面附近的圆形轨道运行周期为T₂，火星质量与地球质量之比为p，火星半径与地球半径之比为q，则T₁与T₂之比为(　)

A.　 　　　　　　　　　　　　　　　　　 B.　

C.　 　　　　　　　　　　　　　　　　　 D.

答案：D

解析：对火星探测器G＝m₁R₁解得T₁＝2π.对神舟飞船G＝m₂R₂解得T₂＝2π，则＝＝，选项D正确．

12．(2010·安徽理综)为了对火星及其周围的空间环境进行探测，我国预计于2011年10月发射第一颗火星探测器“萤火一号”．假设探测器在离火星表面高度分别为h₁和h₂的圆轨道上运动时，周期分别为T₁和T₂.火星可视为质量分布均匀的球体，且忽略火星的自转影响，万有引力常量为G.仅利用以上数据，可以计算出(　)

A．火星的密度和火星表面的重力加速度

B．火星的质量和火星对“萤火一号”的引力

C．火星的半径和“萤火一号”的质量

D．火星表面的重力加速度和火量对“萤火一号”的引力

答案：A

解析：由“萤火一号”分别在两个不同的圆轨道上做匀速圆周运动可知：G＝m²(h₁+R)；

G＝m²(h₂+R)，两式联立可求得火星的质量M与火星的半径R，由火星的半径R可求出火星的体积，进一步求出火星的密度，再根据黄金公式：GM＝gR²，可求得火星表面处的重力加速度g，故A项对．

11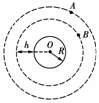．如图所示，A是地球的同步卫星，另一卫星B的圆形轨道位于赤道平面内，离地面高度为h，已知地球半径为R，地球自转角速度为ω₀，地球表面的重力加速度为g，O为地球中心．

(1)求卫星B的运动周期；

(2)若卫星B运行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、B、A在同一直线上)，则至少经过多少时间，它们再一次相距最近？

答案：(1)2π　(2)

解析：根据万有引力提供向心力，列出万有引力与周期的关系，即可求出卫星B的运行周期．第二问关键是要寻找A、B两卫星再一次相距最近时它们转过的角度关系，只要分析出A、B两卫星哪一个角速度大，就能确定相同时间内A、B转过的角度之间的关系．

(1)设卫星B的运行周期为T_B，由万有引力定律和向心力公式得

G＝m(R+h)，①

G＝mg，②

联立①②得T_B＝2π.③

(2)用ω表示卫星的角速度，r表示卫星的轨道半径，由万有引力定律和向心力公式得G＝mrω²，④

联立②④得ω＝，⑤

因为r_A>r_B，所以ω₀<ω_B，用t表示所需的时间

(ω_B－ω₀)t＝2π，⑥

由③得ω_B＝，⑦

代入⑥得t＝.

10．黑洞是爱因斯坦的广义相对论中预言的一种特殊天体，它的密度极大，对周围的物质有极强的吸引力．根据爱因斯坦理论，光子是有质量的，光子到达黑洞表面时也将被吸入，最多恰能绕黑洞表面做匀速圆周运动．根据天文观测，银河系中心可能有一个黑洞，距该黑洞6.0×10¹² m远的星体正以2.0×10⁶ m/s的速度绕它旋转，据此估算黑洞的最大半径为多大．(保留一位有效数字)

答案：3×10⁸ m

解析：对围绕黑洞做圆周运动的星体应用牛顿第二定律得＝

即GM＝v²r

由黑洞特点可知，光子到达黑洞表面最多恰能绕黑洞表面做匀速圆周运动，对光子应用牛顿第二定律，得≥

即R＝

所以R＝＝m≈3×10⁸ m.

9．(2009·福建理综)“嫦娥一号”月球探测器在环绕月球运行过程中，设探测器运行的轨道半径为r，运行速率为v，当探测器在飞越月球上一些环形山中的质量密集区的上空时

(　)

A．r、v都将略为减小

B．r、v都将保持不变

C．r将略为减小，v将略为增大

D．r将略为增大，v将略为减小

答案：C

解析：当探测器飞越月球上一些环形山中的质量密集区的上空时，相当于探测器和月球重心间的距离变小了，由万有引力定律F＝可知，探测器所受月球的引力将增大，这时的引力略大于探测器以原来轨道半径运行所需要的向心力，探测器将做靠近圆心的运动，使轨道半径略为减小，而且月球的引力对探测器做正功，使探测器的速度略微增加，故A、B、D错误，C正确．

8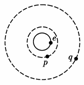．(2008·四川延考)如图，地球赤道上的山丘e，近地资源卫星p和同步通信卫星q均在赤道平面上绕地心做匀速圆周运动．设e、p、q的圆周运动速率分别为v₁、v₂、v₃，向心加速度分别为a₁、a₂、a₃，则(　)

A．v₁>v₂>v₃　 　　　　　　　　　　　　　 B．v₁<v₂<v₃

C．a₁>a₂>a₃　 　　　　　　　　　　　　　 D．a₁<a₃<a₂

答案：D

解析：v₂、v₃均为卫星的在轨运行速度，由G＝m可得v＝，所以轨道半径越大，线速度越小，故v₂>v₃.q是同步卫星，其角速度与e相等，所以由v＝ωr可知v₃>v₁.因此v₂>v₃>v₁，A、B均错．由G＝ma可知半径大的向心加速度小，故a₃<a₂.根据a＝ω²r可知a₁<a₃.因此a₁<a₃<a₂，C错，D正确．

7．我国于2010年11月1日成功将第6颗北斗导航卫星送入太空，预计在2015年建成由30多颗卫星组成的“北斗二号”卫星导航定位系统，此系统由中轨道、高轨道和同步轨道卫星等组成．现在正在服役的“北斗一号”卫星定位系统的三颗卫星都定位在距地面36 000 km的地球同步轨道上．而美国的全球卫星定位系统(简称GPS)由24颗卫星组成，这些卫星距地面的高度均为20 000 km.则下列说法中正确的是(　)

A．“北斗一号”系统中的三颗卫星的质量必须相等

B．GPS的卫星比“北斗一号”的卫星周期短

C．“北斗二号”中的每颗卫星一定比“北斗一号”中的每颗卫星的加速度大

D．“北斗二号”中低轨道卫星的线速度大于高轨道卫星的线速度

答案：BD

解析：卫星做圆周运动的轨道半径与质量无关，选项A错误．由G＝mr可知轨道半径越大，周期越大，选项B正确．“北斗二号”中的同步卫星与“北斗一号”中卫星加速度相同，选项C错误．由G＝m得v＝，所以轨道半径越小，卫星的线速度越大，选项D正确．

6．天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星．双星系统在银河系中很普遍．利用双星系统中两颗恒星的运行特征可推算出它们的总质量．已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动，周期均为T，两颗恒星之间的距离为r，试推算这个双星系统的总质量．(引力常量为G)

答案：

解析：设两颗恒星的质量分别为m₁、m₂，做圆周运动的半径分别为r₁、r₂，角速度分别为ω₁、ω₂.根据题意有

ω₁＝ω₂①

r₁+r₂＝r②

根据万有引力定律和牛顿运动定律，有

G＝m₁ω₁²r₁③

G＝m₂ω₂²r₂④

联立以上各式解得r₁＝r⑤

根据角速度与周期的关系知ω₁＝ω₂＝⑥

联立③⑤⑥式解得m₁+m₂＝.⑦