5．(2010·临沂模拟)我国自主研发、设计和建设的晋东南-南阳-荆门1 000千伏特高压交流试验示范工程投运．工程一直保持安全稳定运动．如图为高压输电简化图，在A、B、C、D四点，电缆线与竖直方向的夹角都是60°，已知电缆线能承受的最大拉力为2 000 N，则AB或CD段电缆线质量应不超过(　)

A．100 kg　 　　　　　　　　　　　　　　　 B．200 kg　

C．400 kg　 　　　　　　　　　　　　　　　 D．800 kg

答案：B

解析：对AB电缆线的左半部分进行受力分析如图所示，对拉力F_T分解并利用平衡条件有：F_Tcos 60°＝，所以AB或CD段电缆线的质量不应超过200 kg，B正确．

4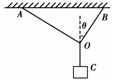．如图所示，轻绳AO和BO共同吊起质量为m的重物．AO与BO垂直，BO与竖直方向的夹角为θ，OC连接重物，则(　)

A．AO所受的拉力大小为mgtan θ

B．AO所受的拉力大小为

C．BO所受的拉力大小为mgcos θ

D．BO所受的拉力大小为

答案：C

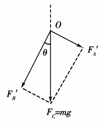
解析：结点O受到的绳OC的拉力F_C等于重物所受重力mg，将拉力F_C沿绳AO和BO所在直线进行分解，两分力分别等于拉力F_A和F_B，如图所示，由力的图示解得：F_A＝F_A′＝mgsin θ，F_B＝F_B′＝mgcos θ.

3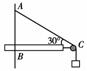．(2010·南平模拟)如图所示，水平横杆BC的B端固定，C端有一定滑轮，跨在定滑轮上的绳子一端悬一质量为m的物体，另一端固定在A点，当物体静止时，∠ACB＝30°，不计定滑轮摩擦和绳子的质量，这时，定滑轮作用于绳子的力等于(　)

A．mg　 　　　　　　　　　　　　　　　　　　　　　 B.mg　

C.mg　 　　　　　　　　　　　　　　　　　 D.mg

答案：A

解析：滑轮所受绳子的作用力是滑轮两侧绳子拉力的合力．根据定滑轮的特点，两侧绳的拉力均为F＝mg.由于两侧绳的夹角为120°，它们的合力也等于mg，即绳子作用于滑轮的力为mg，由牛顿第三定律可知，定滑轮作用于绳子的力也为mg，选项A正确．

2．(2009·海南)两个大小分别为F₁和F₂(F₂<F₁)的力作用在同一质点上，它们的合力的大小F满足(　)

A．F₂≤F≤F₁　 　　　　　　　　　　　 B.≤F≤

C．F₁－F₂≤F≤F₁+F₂　 　　　　　 D．F₁²－F₂²≤F²≤F₁²+F₂²

答案：C

解析：共点的两个力合成，同向时最大，为F₁+F₂，反向时最小，为F₁－F₂.

1．2011年广州亚运会，我国运动员陈一冰勇夺吊环冠军，其中有一个高难度的动作就是先双手撑住吊环，然后身体下移，双臂缓慢张开到如图所示位置，则在两手之间的距离增大过程中，吊环的两根绳的拉力F_T(两个拉力大小相等)及它们的合力F的大小变化情况为

(　)

A．F_T增大，F不变　

B．F_T增大，F增大

C．F_T增大，F减小　

D．F_T减小，F不变

答案：A

解析：由平衡条件，合力F等于人的重力，F恒定不变；当两手间距离变大时，绳的拉力的夹角由零变大，由平行四边形定则知，F_T变大，A正确．

13．(2010·山东理综)如图所示，质量分别为m₁、m₂的两个物体通过轻弹簧连接，在力F的作用下一起沿水平方向做匀速直线运动(m₁在地面，m₂在空中)，力F与水平方向成θ角．则m₁所受支持力F_N和摩擦力f正确的是(　)

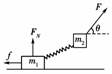
A．F_N＝m₁g+m₂g－Fsin θ

B．F_N＝m₁g+m₂g－Fcos θ

C．f＝Fcos θ

D．f＝Fsin θ

答案：AC

解析：对于m₁、m₂和轻弹簧组成的系统受力分析如图，由平衡条件知：

水平方向：f＝Fcos θ

竖直方向：F_N+Fsin θ＝m₁g+m₂g.

由以上两式得：f＝Fcos θ，F_N＝m₁g+m₂g－Fsin θ，正确选项为A、C.

12．(2010·课标全国)如图所示，一物块置于水平地面上．当用与水平方向成60°角的力F₁拉物块时，物块做匀速直线运动；当改用与水平方向成30°角的力F₂推物块时，物块仍做匀速直线运动．若F₁和F₂的大小相等，则物块与地面之间的动摩擦因数为(　)

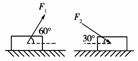
A.－1　 　　　　　　　　　　　　　　　　 B．2－　

C.－　 　　　　　　　　　　　　　 　　　 D．1－

答案：B

解析：由力的平衡条件，F₁cos 60°＝μ(mg－F₁·sin 60°)；F₂cos 30°＝μ(mg+F₂·sin 30°)；再由F₁＝F₂解得μ＝2－.故B项正确．

0．45G≤F≤0.72G.

11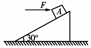．如图所示，将重为G的物体A放在倾角为30°的斜面上，A与斜面间的动摩擦因数μ＝0.1，那么对A施加一个多大的水平力F，可使A物体保持静止？(设A所受最大静摩擦力与滑动摩擦力大小相等)

答案：0.45G≤F≤0.72G

解析：当物体A有沿斜面向上的运动趋势时，其受力如图甲所示．

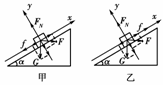
沿斜面、垂直斜面建立坐标系，由平衡条件得：

在x轴上：Fcos α＝Gsin α+f①

在y轴上：F_N＝Fsin α+Gcos α②

且摩擦力f_m＝μF_N③

由以上三式得：F＝＝0.72G

当物体A有沿斜面向下的运动趋势时，其受力如图乙所示．

在x轴上：Fcos α+f＝Gsin α④

在y轴上：F_N＝Gcos α+Fsin α⑤

且摩擦力f_m＝μF_N⑥

由④⑤⑥得作用力F＝＝0.45G

考虑两个结果可知，水平力F的取值范围为

10．如图所示，重为G的均匀链条，两端用等长的轻绳连接，挂在等高的地方，轻绳与水平方向成θ角．试求：

(1)绳子的拉力；

(2)链条在最低点的相互拉力的大小．

答案：(1)G/(2sin θ)　(2)Gcot θ/2

解析：(1)先用整体法，以整个链条为研究对象，链条受重力G和两端轻绳的拉力F₁、F₂的作用，此三力必相交于一点O，如图甲所示．则有：

F₁cos θ＝F₂cos θ，即F₁＝F₂.

F₁sin θ+F₂sin θ＝G，解得F₁＝F₂＝G/(2sin θ)．

(2)再用隔离法，以链条的左半部为研究对象，如图乙所示，左半部链条受到的重力为G/2，受到绳的拉力F₁，受到右半部链条的拉力F的作用，此三力相交于一点O′，则有：

F＝F₁cos θ，G/2＝F₁sin θ.

解得F＝Gcot θ.