
题目列表(包括答案和解析)
20.(2011丰台期末)滑板运动是青少年喜爱的一项活动。如图16所示,滑板运动员以某一初速度从A点水平离开h=0.8m高的平台,运动员(连同滑板)恰好能无碰撞的从B点沿圆弧切线进入竖直光滑圆弧轨道,然后经C点沿固定斜面向上运动至最高点D。圆弧轨道的半径为1m,B、C为圆弧的两端点,其连线水平,圆弧对应圆心角θ=106°,斜面与圆弧相切于C点。已知滑板与斜面问的动摩擦因数为μ =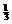 ,g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,运动员(连同滑板)质量为50kg,可视为质点。试求:
,g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,运动员(连同滑板)质量为50kg,可视为质点。试求:
(1)运动员(连同滑板)离开平台时的初速度v0;
(2)运动员(连同滑板)通过圆弧轨道最底点对轨道的压力;
(3)运动员(连同滑板)在斜面上滑行的最大距离。
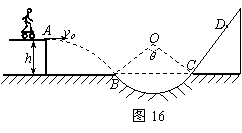
解:(1)运动员离开平台后从A至B在竖直方向有:
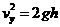 ①
…………(1分)
①
…………(1分)
在B点有: 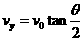 ②
…………(1分)
②
…………(1分)
由①②得: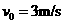 ③
…………(2分)
③
…………(2分)
(2)运动员在圆弧轨道做圆周运动
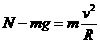 ④
…………(1分)
④
…………(1分)
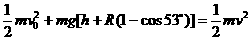 ⑤ …………(1分)
⑤ …………(1分)
联立③④⑤解得N=2150N …………(1分)
(3)运动员从A至C过程有:
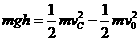 ⑥
…………(1分)
⑥
…………(1分)
运动员从C至D过程有:
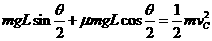 ⑦ …………(1分)
⑦ …………(1分)
由③⑥⑦解得:
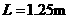 …………(1分)
…………(1分)
19.(2011东城期末)(10分)如图所示,用恒力F使一个质量为m的物体由静止开始沿水平地面移动了位移x,力F跟物体前进的方向的夹角为α,物体与地面间的动摩擦因数为μ,求:
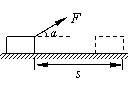 (1)拉力F对物体做功W的大小;
(1)拉力F对物体做功W的大小;
(2)地面对物体的摩擦力f的大小;
(3)物体获得的动能Ek。
(1)物体在F的作用下,发生位移s,F与s的夹角为α,有
WF=Fscosα (3分)
(2)物体对地面的压力为N,由滑动摩擦力公式
f=μN
N=mg-Fsinα
可得f=μ(mg-Fsinα) (4分)
(3)由动能定理
-Wf+ WF=Ek
Ek= Fscosα-μ(mg-Fsinα)s (3分)
18.(2011房山期末)质量为8×107kg的列车,从某处开始进站并关闭发动机,只在恒定阻力作用下减速滑行.已知它开始滑行时的初速度为20m/s,当它滑行了300m时,速度减小到10m/s,接着又滑行了一段距离后刚好到达站台停下,那么:
(1)关闭动力时列车的初动能为多大?
(2)列车受到的恒定阻力为多大?
(3)列车进站滑行的总时间为多大?
解:(1)列车的初动能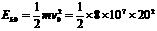 J=1.6×1010 J……………(2分)
J=1.6×1010 J……………(2分)
(2)由动能定理有: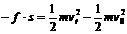 …………………………(2分)
…………………………(2分)
解得列车受到的阻力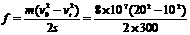 N=4×107N……………………………(1分)
N=4×107N……………………………(1分)
(3)由动量定理有:-f•t=mvt –mv0……………………………(2分)
解得列车滑行的总时间
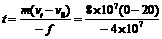 s=40 s………………………(1分)
s=40 s………………………(1分)
17.(2011石景山一模)(18分)一轻质细绳一端系一质量为 m = 0.05 kg
的小球A,另一端套在光滑水平细轴O上,O到小球的距离为 L = 0.1 m,小球与水平地面接触,但无相互作用。在球的两侧等距离处分别固定一个光滑的斜面和一个挡板,二者之间的水平距离S = 2 m,如图所示。现有一滑块B,质量也为m,从斜面上高度h = 3 m处由静止滑下,与小球和挡板碰撞时均没有机械能损失。若不计空气阻力,并将滑块和小球都视为质点,滑块B与水平地面之间的动摩擦因数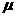 = 0.25,g取 10 m/s2。求:
= 0.25,g取 10 m/s2。求:
(1)滑块B与小球第一次碰撞前瞬间,B速度的大小;
(2)滑块B与小球第一次碰撞后瞬间,绳子对小球的拉力;
(3)小球在竖直平面内做完整圆周运动的次数。

解析:(1) 滑块B从斜面高度h处滑下与小球第一次碰撞前瞬间速度为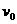 ,由动能定理得:
,由动能定理得:
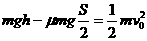 ……………………………………………(3分)
……………………………………………(3分)
求得: 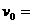
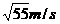 =7.4m/s ……………………………………………(1分)
=7.4m/s ……………………………………………(1分)
(2)滑块B与小球碰撞,没有机械能损失,由动量守恒和机械能守恒得:
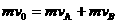 …………………………………………………(1分)
…………………………………………………(1分)
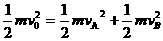 …………………………………………(1分)
…………………………………………(1分)
求得:
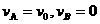 。即碰后滑块B与小球A交换速度。……………(1分)
。即碰后滑块B与小球A交换速度。……………(1分)
对小球由牛顿第二定律得:
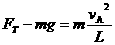 ……………………………………………………(2分)
……………………………………………………(2分)
求得: 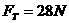 ………………………………………………………(1分)
………………………………………………………(1分)
(3)小球恰能完成一次完整的圆周运动,设它到最高点的速度为v1,小球在最低点速度为v,则有
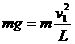 …………………………………………………………(2分)
…………………………………………………………(2分)
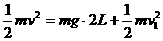 …………………………………………(1分)
…………………………………………(1分)
求得: 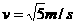 ………………………………………………………(1分)
………………………………………………………(1分)
小球做完整圆周运动时,碰后的速度至少为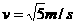 ,由于滑块B与小球A碰后交换速度,则滑块B最终速度至少也为
,由于滑块B与小球A碰后交换速度,则滑块B最终速度至少也为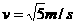 ,经过的路程为
,经过的路程为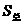 ,则:
,则:
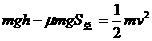 ……………………………………………(2分)
……………………………………………(2分)
求得: 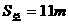 ……………………………………………………………(1分)
……………………………………………………………(1分)
小球做完整的圆周运动的次数为: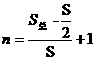
求得: 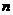 = 6 ……………………………………………………………(1分)
= 6 ……………………………………………………………(1分)
16.(2011石景山一模)(16分)如图所示,水平地面上放有质量均为 = 1 kg的物块A和B,两者之间的距离为
= 1 kg的物块A和B,两者之间的距离为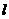 = 0.75 m。A、B与地面的动摩擦因数分别为
= 0.75 m。A、B与地面的动摩擦因数分别为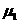 = 0.4、
= 0.4、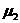 = 0.1。现使A获得初速度
= 0.1。现使A获得初速度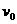 向B运动,同时对B施加一个方向水平向右的力
向B运动,同时对B施加一个方向水平向右的力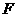 = 3 N,使B由静止开始运动。经过一段时间,A恰好追上B。g
取 10 m/s2。求:
= 3 N,使B由静止开始运动。经过一段时间,A恰好追上B。g
取 10 m/s2。求:
 (1)B运动加速度的大小
(1)B运动加速度的大小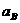 ;
;
(2)A初速度的大小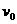 ;
;
(3)从开始运动到A追上B的过程中,
力F对B所做的功。
解:(1)对B,由牛顿第二定律得:
 ……………………………………………………(2分)
……………………………………………………(2分)
求得: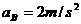 …………………………………………………………(2分)
…………………………………………………………(2分)
(2)设A 经过t时间追上B,对A,由牛顿第二定律得:
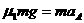 …………………………………………………………(1分)
…………………………………………………………(1分)
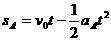 ……………………………………………………(1分)
……………………………………………………(1分)
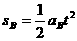 …………………………………………………………(1分)
…………………………………………………………(1分)
恰好追上的条件为:
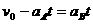 ………………………………………………………(2分)
………………………………………………………(2分)
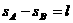 …………………………………………………………(2分)
…………………………………………………………(2分)
代入数据解得: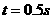 ,
,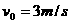 ……………………………………………(1分)
……………………………………………(1分)
(3)
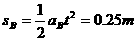 ……………………………………………(2分)
……………………………………………(2分)
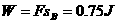 …………………………………………………(2分)
…………………………………………………(2分)
15.(2011怀柔一模)(18分)有一颗地球卫星,绕地球做匀速圆周运动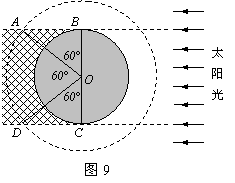 卫星与地心的距离为地球半径
卫星与地心的距离为地球半径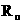 的2倍,卫星圆形轨道平面与地球赤道平面重合。卫星上的太阳能收集板可以把光能转化为电能,太阳能收集板的面积为
的2倍,卫星圆形轨道平面与地球赤道平面重合。卫星上的太阳能收集板可以把光能转化为电能,太阳能收集板的面积为 ,在阳光下照射下每单位面积提供的最大电功率为
,在阳光下照射下每单位面积提供的最大电功率为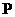 。已知地球表面重力加速度为
。已知地球表面重力加速度为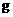 ,近似认为太阳光是平行光,试估算:
,近似认为太阳光是平行光,试估算:
(1) 卫星做匀速圆周运动的周期;
(2) 卫星绕地球一周,太阳能收集板工作时间
(3)太阳能收集板在卫星绕地球一周的时间内最多转化的电能?
(1)(8分)地球卫星做匀速圆周运动,根据牛顿第二定律:
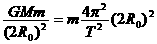 ① ……………………… (3分)
① ……………………… (3分)
在地球表面有: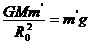
 ② ………………………(3分)
② ………………………(3分)
∴ 卫星做匀速圆周运动的周期为:③
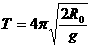 ④ ………………………………………(2分)
④ ………………………………………(2分)
(2)(6分)如图,当卫星在阴影区时不能接受阳光,据几何关系:
∠AOB
= ∠COD =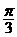 ⑤
………………………(3分)
⑤
………………………(3分)
∴卫星绕地球一周,太阳能收集板工作时间为:
t = T=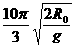 ⑥ …………………………………(3分)
⑥ …………………………………(3分)
(3(4分))最多转化的电能:
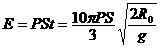 ⑦
…………………… (4分)
⑦
…………………… (4分)
14.(2011怀柔一模)(16分)一滑块经水平轨道AB,进入竖直平面内的四分之一圆弧轨道BC。已知滑块的质量m=0.60kg,在A点的速度vA=8.0m/s,AB长x=5.0m,滑块与水平轨道间的动摩擦因数μ=0.15,圆弧轨道的半径R=2.0m,滑块离开C点后竖直上升h=0.20m,取g=10m/s2。求:
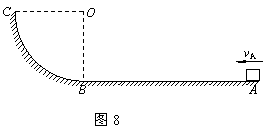 (1)滑块经过B点时速度的大小;
(1)滑块经过B点时速度的大小;
(2) 滑块经过B点时圆弧轨道对它的支持力的 大小;
(3)滑块在圆弧轨道BC段克服摩擦力所做的功。
(1)(5分)滑块从A到B,做匀减速直线运动,
由动能定理:
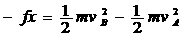 ① ………………………(2分)
① ………………………(2分)
摩擦力 f=μmg ② ………………………(2分)
联立上式,解得
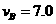 m/s ③ ………………………(1分)
m/s ③ ………………………(1分)
(2)(5分)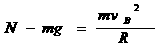 ④ ………………(2分)
④ ………………(2分)
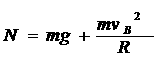 ⑤ ………………………………(2分)
⑤ ………………………………(2分)
N=20.7N ………………………(1分)
(3)(6分)滑块离开C点后做竖直上抛运动,由运动学公式
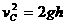 ⑥ ………………………………(2分)
⑥ ………………………………(2分)
从B到C的过程中,摩擦力做功Wf ,由动能定理
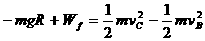 ⑦ ………………(2分)
⑦ ………………(2分)
联立③⑥⑦式,解得 Wf = -1.5J …………………(1分)
克服摩擦力做功W’f=1.5J …………………(1分)
13. (2011丰台一模)(20分) 如图所示,P为质量为m=1kg的物块,Q为位于水平地面上
(2011丰台一模)(20分) 如图所示,P为质量为m=1kg的物块,Q为位于水平地面上
的质量为M=4kg的特殊平板,平板与地面间的动摩因数μ=0.02。在板上表面的上方,存在一定厚度的“相互作用区域”,区域的上边界为MN。P刚从距高h=5m处由静止开始自由落下时,板Q向右运动的速度为vo=4m/s。当物块P进入相互作用区域时,P、Q之间有相互作用的恒力F=kmg,其中Q对P的作用竖直向上,k=21,F对P的作用使P刚好不与Q的上表面接触。在水平方向上,P、Q之间没有相互作用力,板Q足够长,空气阻力不计。
( 取g=10m/s2,以下计算结果均保留两位有效数字)求:
(1)P第1次落到MN边界的时间t和第一次在相互作用区域中运动的时间T;
(2)P第2次经过MN边界时板Q的速度v;
(3)从P第1次经过MN边界到第2次经过MN边界的过程中,P、Q组成系统损失的机械能△E;
(4)当板Q速度为零时,P一共回到出发点几次?
解:(1) (8分)
P自由落下第一次到达边界MN时
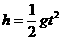
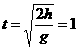 s (2分)
s (2分)
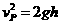
P到达边界MN时速度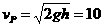 m/s (2分)
m/s (2分)
P进入相互作用区域时,kmg - mg = ma a = (k - 1)g = 200m/s2 (2分)
P第一次进入相互作用区域减速到零后又向上加速,以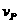 速度大小再次越过MN,所以运动时
速度大小再次越过MN,所以运动时
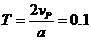 s (2分)
s (2分)
(2) (4分)
上面分析知P先自由下落,以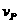 进入相互作用区域,减速到零后又向上加速,以
进入相互作用区域,减速到零后又向上加速,以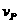 速度大小再次越过MN,然后做竖直上抛运动回到原出发点,接着又重复上述运动过程。
速度大小再次越过MN,然后做竖直上抛运动回到原出发点,接着又重复上述运动过程。
每当P从出发点运动到MN的时间t内,板Q加速度
a1向左,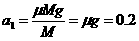 m/s2 (1分)
m/s2 (1分)
每当P在相互作用区中运动的时间T内,板Q加速度a2向左
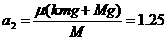 m/s2 (1分)
m/s2 (1分)
P第2次经过MN边界时,板Q的速度
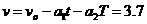 m/s (2分)
m/s (2分)
(3)(4分)
P第1次经过MN边界时,板Q的速度
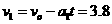 m/s
(2分)
m/s
(2分)
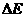 =
=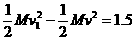 J
(2分)
J
(2分)
(4) (4分)
设板Q速度为零时,P一共回到出发点n次。由以上分析得:
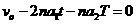 (2分)
(2分)
代入数据,解得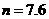 故n取7
(2分)
故n取7
(2分)
12.(2011朝阳一模)(16分)如图所示,摩托车运动员做特技表演时,以v0=9.0m/s的初速度冲向高台,然后从高台水平飞出。若摩托车冲向高台的过程中牵引力的平均功率P=4.0kW,冲到高台顶端所用时间t=3.0s,人和车的总质量m=1.5×102kg,高台顶端距地面的高度h=7.2m,摩托车落地点到高台顶端的水平距离x=10.8m。不计空气阻力,取g=10m/s2。求:
(1)摩托车从高台顶端飞出到落地所用时间;
(2)摩托车落地时速度的大小;
(3)摩托车冲上高台的过程中克服摩擦阻力所做的功。

解:(1)设摩托车在空中的飞行时间为t1,则有
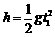
解得 t1=1.2s 4分
(2)摩托车做平抛运动的水平速度

落地时摩托车在竖直方向的速度
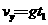 =12m/s
=12m/s
摩托车落地时的速度
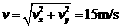 6分
6分
(3)设摩托车冲上高台的过程中,克服摩擦阻力所做的功为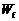 。摩托车冲向高台的过程中,根据动能定理有
。摩托车冲向高台的过程中,根据动能定理有
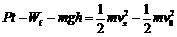
解得 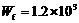 J
6分
J
6分
11.(2011西城一模)(16分)一滑块(可视为质点)经水平轨道AB进入竖直平面内的四分之一圆弧形轨道BC。已知滑块的质量m=0.50kg,滑块经过A点时的速度υA=5.0m/s,AB长x=4.5m,滑块与水平轨道间的动摩擦因数μ=0.10,圆弧形轨道的半径R=0.50m,滑块离开C点后竖直上升的最大高度h=0.10m。取g=10m/s2。求
(1)滑块第一次经过B点时速度的大小;
(2)滑块刚刚滑上圆弧形轨道时,对轨道上B点压力的大小;
(3)滑块在从B运动到C的过程中克服摩擦力所做的功。

(1)滑块从A到B做匀减速直线运动,摩擦力 f=μmg (1分)
由牛顿第二定律可知,滑块的加速度大小 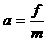 (1分)
(1分)
由运动学公式 υB2﹣υA2 =﹣2 a x (1分)
解得滑块经过B点时速度的大小 υB = 4.0 m/s (2分)
(2)在B点,滑块开始做圆周运动,由牛顿第二定律可知
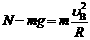 (2分)
(2分)
解得轨道对滑块的支持力 N = 21N (2分)
根据牛顿第三定律可知,滑块对轨道上B点压力的大小也为21N。(1分)
(3)从B到滑块经过C上升到最高点的过程中,由动能定理
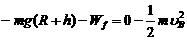 (3分)
(3分)
解得滑块克服摩擦力做功Wf =1.0J (3分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com