
题目列表(包括答案和解析)
33. (7分)如图12甲所示,闭合开关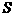 ,滑动变阻器取四个不同阻值时,可以得出电流表和电压表的四组对应的值。这四组对应的值在图乙的
,滑动变阻器取四个不同阻值时,可以得出电流表和电压表的四组对应的值。这四组对应的值在图乙的 坐标中分别用
坐标中分别用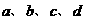 四个点表示(坐标原点表示的电压值和电流值均为零)。由这四个点作出的
四个点表示(坐标原点表示的电压值和电流值均为零)。由这四个点作出的 图象为一条直线,延长直线交纵轴(
图象为一条直线,延长直线交纵轴(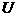 轴)于
轴)于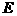 点,交横轴(
点,交横轴( 轴)于
轴)于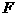 点,若电源电压为
点,若电源电压为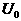 ,定值电阻的阻值为
,定值电阻的阻值为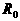 。据此分析:(1)
。据此分析:(1)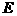 点表示的电流表、电压表的示数各为多少?此时电路处于什么状态?(2)
点表示的电流表、电压表的示数各为多少?此时电路处于什么状态?(2)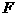 点表示的电压表、电流表的示数各为多少?此时电路处于什么状态?
点表示的电压表、电流表的示数各为多少?此时电路处于什么状态?
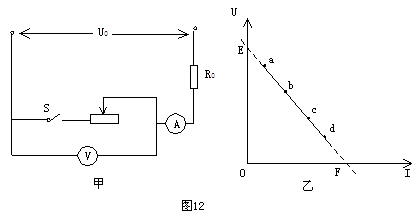
(1)在E点时,电流表示数为零(1分),电压表示数为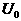 (1分)。此时S断开(1分)。
(1分)。此时S断开(1分)。
(2)在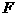 点时,电压表示数为零(1分),电流表示数为
点时,电压表示数为零(1分),电流表示数为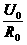 (2分)。此时S闭合且滑动变阻器的滑片P滑到了最左端,使滑动变阻器处于局部短路状态(1分)。
(2分)。此时S闭合且滑动变阻器的滑片P滑到了最左端,使滑动变阻器处于局部短路状态(1分)。
[题目]已知电阻R2的阻值为R1的n倍,灯上标着“6V,3W”字样,当S接a时灯正常发光;当S接b时灯L的功率为接a时功率的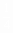 。
求:(1)当n为小于5的正整数时,求n的取值;
(2)R1、R2与n的对应值。
(01年重庆联招题)
解:(1)设电源电压为U,由RL=
。
求:(1)当n为小于5的正整数时,求n的取值;
(2)R1、R2与n的对应值。
(01年重庆联招题)
解:(1)设电源电压为U,由RL=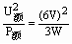 =12Ω。
当S接a时,I1=
=12Ω。
当S接a时,I1=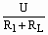 ,则灯的功率为PL=I
,则灯的功率为PL=I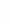 RL=
RL=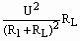 ①
当S接b时,I2=
①
当S接b时,I2=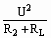 ,则灯的功率为P′L=I
,则灯的功率为P′L=I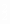 RL=
RL=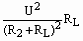 ②
又P′L=
②
又P′L=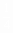 PL,RL=12Ω,R2=nR1,则由①②得R1=
PL,RL=12Ω,R2=nR1,则由①②得R1=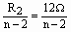 。
又R1>0、n-2>0、n>2,∴2<n<5,n的取值为3、4。
②当n=3时,R1=
。
又R1>0、n-2>0、n>2,∴2<n<5,n的取值为3、4。
②当n=3时,R1=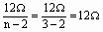 ,R2=nR1=3×12Ω=36Ω。
当n=4时,R1=
,R2=nR1=3×12Ω=36Ω。
当n=4时,R1=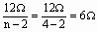 ,R2=nR1=4×6Ω=24Ω。
,R2=nR1=4×6Ω=24Ω。
例2. 将一盏标有“12V、6W”的灯L接入电压为18V的电源上,要使小灯泡正常发光,应在电路中串联一个多大的电阻?此电阻消耗的功率是多少?
解:设串联的电阻为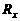 ,电阻消耗的功率为
,电阻消耗的功率为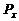 ,灯丝电阻
,灯丝电阻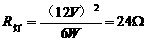
当灯正常发光时,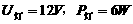
由图2可知: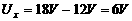
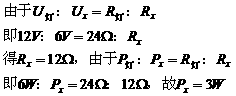

例3. 如图3,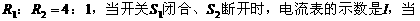
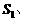
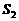 均闭合时,电流表的示数是
均闭合时,电流表的示数是 ,则
,则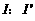 =( )
=( )
A. 5:4 B. 4:5 C. 1:5 D. 5:1
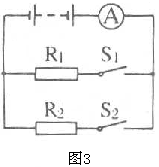
分析:当 断开时,电流表的示数就是通过
断开时,电流表的示数就是通过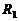 中的电流,即
中的电流,即
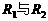 中的电流之和。即
中的电流之和。即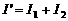 。由于
。由于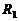 与
与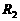 并联,所以
并联,所以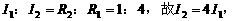
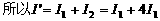
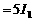 ,故
,故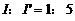 ,选C。
,选C。
例4. 如图4,灯L上标有“4V、2W”的字样,当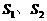 均闭合时,
均闭合时,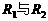 消耗的功率之比为2:1,当
消耗的功率之比为2:1,当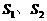 均断开时,
均断开时, 消耗的功率之比为5:1,求
消耗的功率之比为5:1,求 的值。
的值。
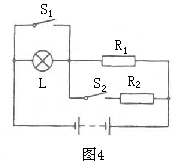
解:灯丝电阻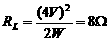

例:如图5所示,当滑动变阻器的滑片P分别在位置a、b(均非端点)时,电压表示数之比为4:3,当P在a时,R0消耗的功率和变阻器消耗的功率之比为1:5。求(1)P在a与P在b时,电流表示数之比。(2)Ra与Rb之比。
解析:在状态a时,
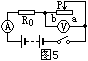
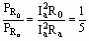
即 (1)
(1)
两状态局部联系为,已知状态变化前后变阻器两端电压之比,即
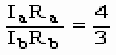
所以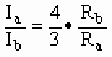 (2)
(2)
根据电源电压不变得:
Ia(R0+Ra)=Ib(R0+Rb)
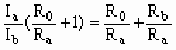
将(1)式代入上式得:
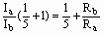 (3)
(3)
(2)、(3)联立解得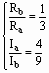
即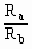 =
=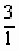 =3
=3
15. (1)P置于中点时,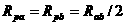 ,两电阻并联,
,两电阻并联,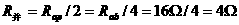 ,因U=6伏,故
,因U=6伏,故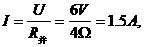
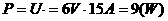
(2)因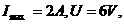 故
故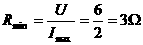
则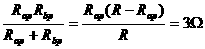
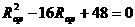
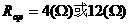 .
.
故P在变阻器的滑动范围是4( )到12
)到12 之间.
之间.
15. 如图17-18所示电路中,滑动变阻器的滑片P把变阻器分为Rap和Rpb两部分,已知变阻器的最大阻值为16欧,电源电压为6伏不变,电流表的最大量程为2安,求:
如图17-18所示电路中,滑动变阻器的滑片P把变阻器分为Rap和Rpb两部分,已知变阻器的最大阻值为16欧,电源电压为6伏不变,电流表的最大量程为2安,求:
(1)P置于变阻器的中点时电流表的示数和变阻器消耗的总功率;
(2)为了电流表的安全使用,变阻器的滑片P在变阻器上滑动的阻值范围.
1、求阻值范围:
[例2] 如图所示电路,滑动变阻器滑片P,把变阻器R分为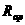 和
和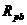 两部分,已知变阻器的最大值为
两部分,已知变阻器的最大值为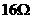 ,电源电压为6V不变,电流表的最大量程为2A。求:
,电源电压为6V不变,电流表的最大量程为2A。求:
(1)P置于变阻器R的中点时,电流表的示数和变阻器消耗的总功率。
(2)为了电流表的安全使用,变阻器的滑片P在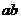 间的阻值范围。
间的阻值范围。
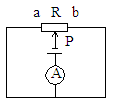
分析:由图可见,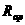 和
和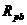 两部分并联,电流表测干路电流,P在中点时,
两部分并联,电流表测干路电流,P在中点时,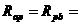
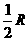 ;要求出P在中点时电流表示数,或用
;要求出P在中点时电流表示数,或用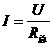 ,或根据并联电路干路电流等于各支路电流之和
,或根据并联电路干路电流等于各支路电流之和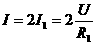 都可求出,变阻器的总功率可根据
都可求出,变阻器的总功率可根据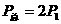 求出。
求出。
为使电流表完全使用,即干路电流不得超过2A,可根据这个电流值,应用欧姆定律求出并联后的总电阻再根据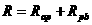 和
和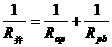 求出P片的滑动范围。
求出P片的滑动范围。
解:
(1)P在R中点时,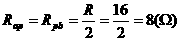 ,电流表示数
,电流表示数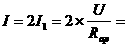
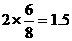 (A)
(A)
变阻器的总功率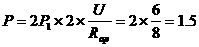 (A)
(A)
(2)电流表量程为2A,为使电流表安全使用,干路电流不得超过2A,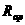 与
与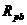 并联后的总电阻
并联后的总电阻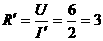 (
( )
)
因为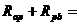 R,
R,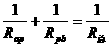 ,所以
,所以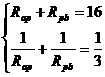
解得: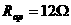 或
或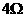 ,
,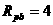
 或12
或12
所以为了电流表的安全使用,P片应在4 -12
-12 间的范围内变化。
间的范围内变化。
2、用极值法:
[例3] 如图所示电路中,电源电压不变,开关S闭合后,两灯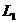 、
、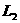 均可发光,当变阻器的滑片P向左移动时( )
均可发光,当变阻器的滑片P向左移动时( )
A. 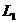 、
、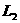 两灯都变暗 B.
两灯都变暗 B.
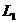 灯变亮,
灯变亮,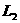 变暗
变暗
C. 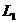 灯变暗,
灯变暗,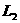 灯变亮 D.
灯变亮 D.
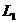 、
、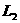 两灯都变亮
两灯都变亮

分析:本题用极值法分析较简单,当P在最右端时,变阻器全部连入电路,电路总电阻最大,在电源电压不变的情况下,干路电流最小,设电灯电阻不变,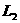 两端电压
两端电压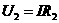 最小,L1两端电压最大,所以此时L1最亮,L2最暗。在P向左端移动时,变阻器连入电路的电阻逐渐变小,P达到最左端时,变阻器连入电路的电阻为零,L1被短路,L1不发光,电源电压全部加在灯L2两端,L2两端电压最大,通过L2的电流也最大,L2最亮,所以P向左移动L1变暗,L2变亮,C项正确。
最小,L1两端电压最大,所以此时L1最亮,L2最暗。在P向左端移动时,变阻器连入电路的电阻逐渐变小,P达到最左端时,变阻器连入电路的电阻为零,L1被短路,L1不发光,电源电压全部加在灯L2两端,L2两端电压最大,通过L2的电流也最大,L2最亮,所以P向左移动L1变暗,L2变亮,C项正确。
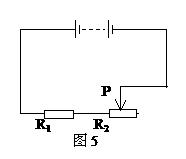
3. 如图5,电源电压不变, 为定值电阻,变阻器的最大阻值是
为定值电阻,变阻器的最大阻值是 的2倍,当滑片P从最左端滑到最右端的过程中,变阻器消耗的电功率( )
的2倍,当滑片P从最左端滑到最右端的过程中,变阻器消耗的电功率( )
A. 一直是逐渐增大 B. 一直是逐渐减小
C. 先增大后减小 D. 先减小后增大
答案:1. D 2. C 3. C
2. 电阻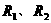 并联时的总电阻是
并联时的总电阻是 ,串联时的总电阻( )
,串联时的总电阻( )
A. 一定是
B. 一定大于 小于
小于
C. 一定不小于
D. 一定不等于
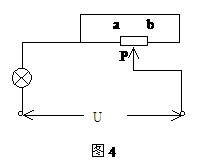
1. 如图4,电源电压不变,当滑动变阻器的滑片P由a端移向b端时,灯的亮度( )
A. 变暗 B. 变亮
C. 先变亮后变暗 D. 先变暗后变亮
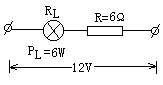 解:如图
解:如图
∵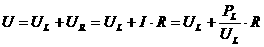
∴12=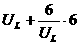
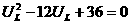
∴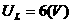
∴ .
.
功率为2瓦的小灯泡与阻值为4欧的电阻串联接在6伏的电源上,灯正常发光.求:灯的电阻和它的额定电压。(请用两种方法做)。
方法一
解:灯泡正常发光,其功率是2W
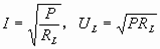
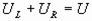
即: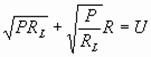
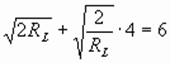
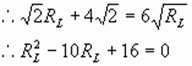
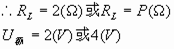
方法二
解: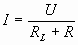
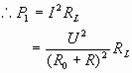
即: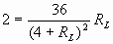
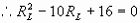
同样可以求得: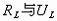 的值
的值
二次函数求解法
[例1]如图3所示的电路,电源电压恒定,已知R1=10欧,R2是滑动变阻器,最大阻值为50欧,当滑动变阻器的滑片P由a端滑到b端的过程中,滑动变阻器消耗的功率是( )
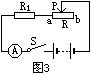 A、逐渐变大 B、逐渐变小
A、逐渐变大 B、逐渐变小
C、先变大后变小 D、先变小后变大
(2000年厦门市中考)
分析:建立p2与u2滑动变阻器电功率与电压的关系式,利用二次函数知识求解。
因p2=u2·I=u2·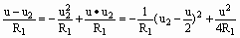 。
上式可视为一个二次函数,当u2=
。
上式可视为一个二次函数,当u2=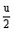 时,p2有最大值
时,p2有最大值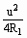 ,因R1、R2串联,所以有
,因R1、R2串联,所以有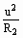 =
=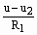 ,可得此时R2=R1。
,可得此时R2=R1。
因R2的最大阻值为50欧,大于R1的阻值10欧,所以当滑片P从a端向b端滑动时,变阻器消耗的功率先变大后变小。C正确。 对此类题可总结出一般规律:
设电源电压为u,定值电阻为R1,滑动变阻器R2的阻值变化范围为0-∞,则R2消耗的电功率为: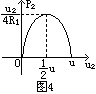 p2=u2·I=u2·
p2=u2·I=u2·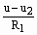 =-
=-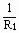 (u2-
(u2-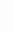 )2+
)2+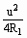 。
。
将上式看作一个二次函数,其图象如图4所示。由图象可知: (1)p2的最大值是由R1和u的大小决定的。 (2)当u2=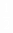 u(即R2=R1)时,p2最大为
u(即R2=R1)时,p2最大为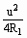 。 (3)当0≤u≤
。 (3)当0≤u≤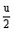 (即0≤R2≤R1)时,该函数为增函数,p2随R2的增大而增大,所以当R2<R1时,R2增大时其功率增大。 (4)当
(即0≤R2≤R1)时,该函数为增函数,p2随R2的增大而增大,所以当R2<R1时,R2增大时其功率增大。 (4)当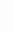 ≤u2<u(即R2>R1)时,此函数为减函数,p2随R2的增大而减小,所以,当R2的最大值大于R1时,p2总是先增大后减小。
≤u2<u(即R2>R1)时,此函数为减函数,p2随R2的增大而减小,所以,当R2的最大值大于R1时,p2总是先增大后减小。
例1.在如图8-2电路中,定值电阻R1与滑动变阻器串联在电源电压为U的电路中,求R2为何值时滑动变阻器消耗功率P2最大?
解: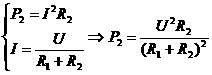 --①
--①
分子、分母都有R2如何分析?
讨论: (1)当R2≥R1时,
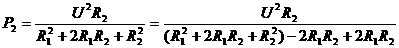 (给分母配方)
(给分母配方)
=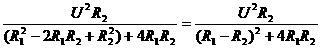
 将上式中分子分母同时除以
将上式中分子分母同时除以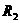 ,则有
,则有
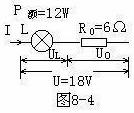
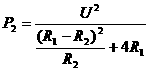 --②在上述电路中,R1、U都是定值.
--②在上述电路中,R1、U都是定值. 公式中R2是自变量,P2是因变量,即R2的函数,因此不难看出:当R2=R1时,R2消耗的功率最大,且最大功率
公式中R2是自变量,P2是因变量,即R2的函数,因此不难看出:当R2=R1时,R2消耗的功率最大,且最大功率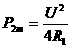 .
.
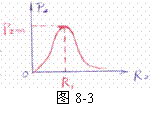
将②式中的函数关系绘制成图象,如右图8-3,当R2=0时,P2=0;当R2由0增至R1过程中,它消耗的功率P2一直在变大;当R2再增大,P2反而逐渐减小.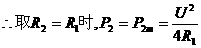 .
.
(2)当R2<R1时,当R2由0增大时,P2始终增大,这就是说:将滑动变阻器滑片P移至阻值最大处,即将R2的全部电阻值都连入电路时,它消耗的电功率最大.由上面①式可知:最大功率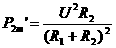 ,公式中的R2为滑动变阻器可连入的最大电阻.
,公式中的R2为滑动变阻器可连入的最大电阻.
例10.如图3所示,R1=10欧,R2的最大电阻值为30欧,电源电压值为8伏,求变阻器R2连入电路的电阻为多大时,R2上消耗的电功率最大?最大为多少?
[解析]
设R2连入电路中的电阻为Rx时,其消耗的电功率最大为P,根据P=I2R有:
P=I2Rx=(U/(Rx+R1))2·Rx,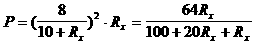 ,根据数学上方程
,根据数学上方程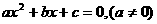 ,有实数根时,△=b2-4ac≥0求解。将上式整理为关于Rx的一元二次方程
,有实数根时,△=b2-4ac≥0求解。将上式整理为关于Rx的一元二次方程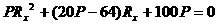 ,因为Rx存在且有正根,所以△=(20P-64)2-4×P×100P≥0,解不等式得P≤1.6瓦,所以R2消耗的最大电功率为1.6瓦,将P=1.6瓦代入原方程可以求得Rx=10Ω。
,因为Rx存在且有正根,所以△=(20P-64)2-4×P×100P≥0,解不等式得P≤1.6瓦,所以R2消耗的最大电功率为1.6瓦,将P=1.6瓦代入原方程可以求得Rx=10Ω。
3、利用两个基本不等式:
例1. 如图1,用一根电阻为 的粗细均匀的电阻丝,绕成一个圆环,用导线在A点固定相接,滑片B与电阻丝接触良好,把它接在电压为12伏的电源上,求滑片至何处时电流表的示数最小,并求这个最小值。
的粗细均匀的电阻丝,绕成一个圆环,用导线在A点固定相接,滑片B与电阻丝接触良好,把它接在电压为12伏的电源上,求滑片至何处时电流表的示数最小,并求这个最小值。
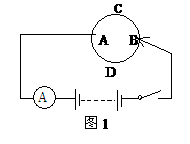
解:设BCA段电阻为 ,则ADB段电阻为
,则ADB段电阻为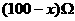 ,因为ACB段与ADB段并联,则
,因为ACB段与ADB段并联,则 ,
, 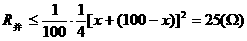 ,
,
式中的等号当且仅当 ,即
,即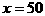 时成立,因此
时成立,因此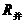 的最大值为
的最大值为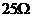 ,于是
,于是
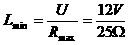
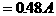
例2. 如图2,电源电压恒定,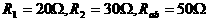 。闭合开关S,滑片P从b端向a端移动的过程中,电路中电流表的示数( )
。闭合开关S,滑片P从b端向a端移动的过程中,电路中电流表的示数( )
A. 逐渐增大 B. 逐渐减少
C. 先增大后减少 D. 先减少后增大
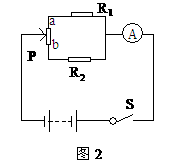
解:设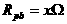 ,则
,则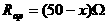 ,电路中的总电阻是由
,电路中的总电阻是由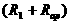 与
与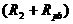 并联而得的总电阻。于是
并联而得的总电阻。于是
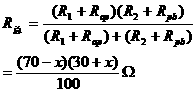
由基本不等式1,得
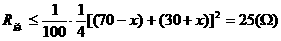
上式中的等号,当且仅当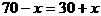 ,即
,即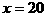 时成立,此时电路中的总电阻最大。可知,滑片P从b端向a端移动的过程中,电路中的总电阻先增大后减小,所以电路中的总电流先减少后增大,即电流表的示数先减小后增大,选D。
时成立,此时电路中的总电阻最大。可知,滑片P从b端向a端移动的过程中,电路中的总电阻先增大后减小,所以电路中的总电流先减少后增大,即电流表的示数先减小后增大,选D。
例3. 将两只电阻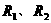 串联接入某电路中,电流是0.4A,若将这两只电阻并联接入同一电路中,则干路的电流至少是多少?
串联接入某电路中,电流是0.4A,若将这两只电阻并联接入同一电路中,则干路的电流至少是多少?
解:设电源电压为U,则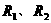 串联时,
串联时,
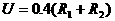 ,
,
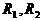 并联时,
并联时,
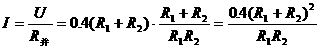
由基本不等式1,有
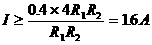
当且仅当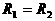 时,
时,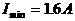
例4. 如图3,定值电阻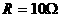 ,滑动变阻器的总阻值
,滑动变阻器的总阻值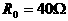 ,a与b为变阻器的上下端点,电源电压U=40V,求滑动变阻器滑到何处时,电流表读数最小?
,a与b为变阻器的上下端点,电源电压U=40V,求滑动变阻器滑到何处时,电流表读数最小?
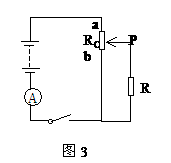
解:设下段电阻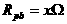 ,由上段电阻
,由上段电阻
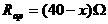
R与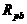 并联的电阻为
并联的电阻为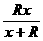 ,于是
,于是
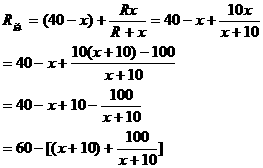
由基本不等式2,得
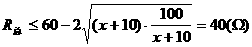
当且仅当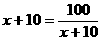 ,即
,即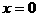 时
时
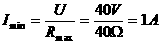
[例1]
电阻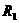 和
和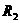 并联后,接在电压为
并联后,接在电压为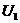 的电源上,消耗的总功率为
的电源上,消耗的总功率为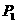 ,将
,将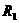 和
和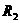 串联后,接在电源电压为
串联后,接在电源电压为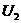 的电源上,消耗的总功率为
的电源上,消耗的总功率为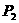 ,若
,若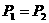 ,下面说法正确的是( )
,下面说法正确的是( )
A. 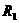 一定等于
一定等于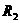 B.
B.
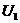 一定等于
一定等于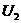
C. 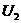 可以小于
可以小于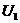 D.
D.
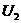 可能等于
可能等于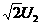
故选C正确
练习:
例1. 电阻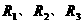 并联,总电流
并联,总电流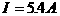 ,又
,又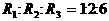 ,求通过
,求通过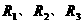 各支路的电流
各支路的电流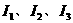
解: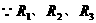 并联
并联
 电压
电压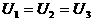
 各支路电流与各支路电阻成反比
各支路电流与各支路电阻成反比
又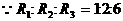
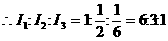
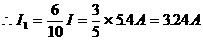
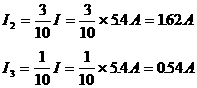
2、利用一元二次方程
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com