7、一只密封的箱子体积是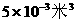，质量是4千克，不慎落入水中，木箱在水中将(　　 )

　　　 A．上浮　　　　　　　 B．下沉　　　　　　　 C．悬浮　　　　　　　 D．无法判断 　　　 8、一木块放入盛满水的容器中，溢出水的质量是10克。若将它放入盛满酒精的容器中，溢出酒精的质量是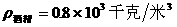：()()(　　　 ) 　　　 A．8克　　　　　　　　 B．10克　　　　 C．12.5克　　　　　　 D．无法确定

5、一个正方体木块漂浮在水面上，水上部分与水下部分体积比为3∶7，则这个木块的密度为　　　　　　　　　 千克/米³_。

 6、把一个木块和一铁块捆在一起放入水中，恰能悬浮，已知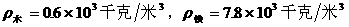，则铁块与木块的质量之比是　　　　　　　　　　 。

4、将铁块浸在水银中，它静止时浸在水银中的体积是总体积的　　　　　　　　 。()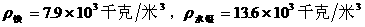

3、某物体浸没在水中时，弹簧平的示数是它在空气中称时的4/5，则物体的密度等于　　　　　　　　　 千克/米³。

2、质量相等的木块和冰块(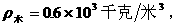

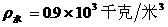)漂浮在水中，木块受到的浮力　　　　　　　　　　 冰块受到的浮力，木块排开水的体积　　　　　　　 　　　 冰排开受到的体积(填“大于”，“等于”“小于”)。

1、将一个物体挂在弹簧秤下，弹簧秤的示数是1.96牛，若把它浸没在水中时，弹簧秤的示数是1.47牛，则此物体的体积为　　　　　　　 米³，物体的密度为　　　　　　　　　 千克/米³。

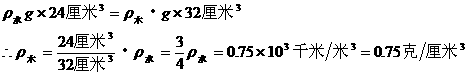
　　　 代入(1)式

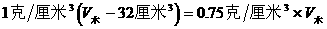
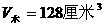
　　　 解法二：漂浮物体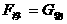

　　　　　　　 ∴

　　　　　　　 ∴

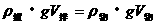
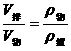
　　　 即漂浮体静止时，被液面分成两部分，其中与物体整体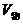之比为物体密度与液体密度之比，而且无论如何切割物体，因为物体密度均匀，密度不改变，那么剩余部分静止时，被液面分成两部分的体积比不变。

　　　 则本题中：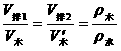

　　　 例6：一个实心小球分别被放入盛有足够多的水和酒精的容器中，小球受到的浮力分别为0.9牛和0.8牛，已知水和酒精的密度之比为5∶4，求小球的密度。

　　　 分析与解：

　　　 在通常求解浮力的题目中，物体浸在液体中的状态，无论是漂浮，悬浮还是沉底，都是已知的，而本题却未知，此题比较新颖和特殊，值得认真研究。

　　　 物块自由投入液体中时：(1)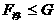；(2)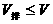。这一规律是计论“隐含物体”浮沉习题的基本出发点。

　　　 解法一：由物体自由投入液体中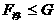：，因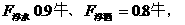

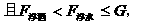小球在酒精中沉底，即。又由题意：

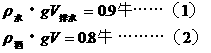
　　　 两式解得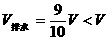：，可知小球在水中漂浮，则。

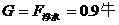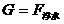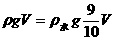　　　 再由，代入公式，得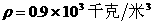

　　　 解法二：由题意：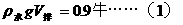

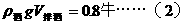
　　　 两式解得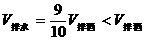：，又因物体投入液体中时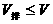，得，故小球在水中漂浮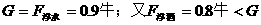，，所以小球在酒精中沉底，即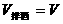，再由。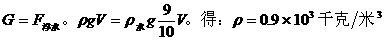

[习题]：

2、浮力的计算

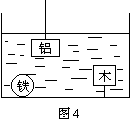
　　　 例1：体积相同的铁球、铝球和木块，浸在液体中的情况如图4所示，则比较它们受到的浮力：

　　　 A．铁球受到的浮力最大

　　　 B．铝球受到的浮力最大

　　　 C．木块受到的浮力最大

　　　 D．它们受到的浮力一样大

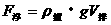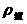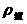　　　 分析与解：根据阿基米德原理可知，物体受到浮力的大小由两个因素决定，一是液体的密度，二是排开液体的体积。铁球 、铝块、木块浸在同一种液体中，相同，且它们的体积相同，全部浸没在液体中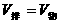，因此它们排开液体的体积相等，所以铁球、铅块、木块受到的浮力一样大。

　　　 正确答案应为D。

　　　 说明：铁球、铝块、木块三个物体的密度不同，重力不同，形状不同，浸在液体中不同深度的地方，但却受到同样大小的浮力。说明浮力说明大小与组成物体的物质的密度，物体的重力、物体的形状及全浸物体在液体中的深度都无关。

　　　 例2：一个物体重为88.2牛，将其放入密度为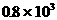千克/米³的液体中静止，受到的浮力为78.4牛，若此物体放入水中静止时，受到的浮力为　　　　　　　　　　 牛。

　　　 分析与解：判断物体有浮沉有两种方法：

　　　 (1)受力比较法：物体静止在水中，有三种情况，如果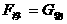，可能漂浮或悬浮，如果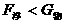，物体处于沉底静止状态。本题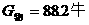，静止在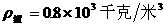的液体中受到浮力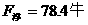则物体在此液体中沉底静止。

　　　 (2)密度比较法：计算出物体的密度，与水的密度相比较，确定其浮沉。

　　　 根据上个状态可计算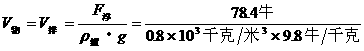　　

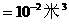
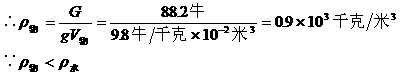
　　　　　　　 ∴物体在水中静止时一定漂浮。

　　　　　　　 ∴浮力与重力平衡，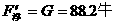

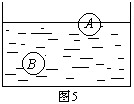
　　　 例3：如图5所示，A、B两物体静止在水中，则：

　　　 A．两物体受到的浮力一定相等。　　

　　　 B．两物体受到的浮力不等，A物体受到的浮力大。

　　　 C．两物体的密度不等，B物体的密度大。

　　　 D．两物体的重力不等，B物体的重力大。

　　　 分析与解：两个物体静止在水中，其中A物体漂浮，B物体悬浮。则它们受到的浮力都与其重力相等。但题目中没有提供它们重力是否相等的条件，因而就不能从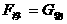比较物体受到的浮力的大小。 　　　 题目中也没说明，A、B两个物体体积大小的情况，因而就不能根据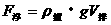来比较物体受到的浮力，也就不能推断出重力的大小。A、B、D三个选项都是错误的。

　　　 本题的正确答案应是C，这是利用物体的密度与液体的密度相比较得出的。

　　　 A物体漂浮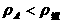：；B物体悬浮：。

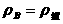　　　 液体的密度相同。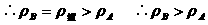

　　　 说明：由于漂浮和悬浮物体在液体中受到的浮力都等于它们受到的重力，所以常常将这两种情况混淆。因而在分析问题时，不但要注意抓住这两类现象的相同点。同时还要特别注意抓住它们之间的不同点，这正是解题的关键。漂浮物体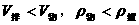。而悬浮的物体，。

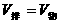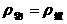　　　 例4：弹簧平下挂一金属块，当金属块浸没在水中时，弹簧秤的示数是29.4牛，这个金属块所受的重力是多少？(已知金属的密度为7.0×10³千克/米³)。

　　　 分析与解：浮力问题的一般解题步骤：

　　　 (1)通过审题明确研究对象，确定它所处的状态。若物体浸没在液体中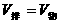，；若物体浮在液面上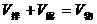，，因此。

　　　 (2)分析研究对象的受力情况，画出力的示意图，在图中标出已知力的符号、量值和未知力的符号。

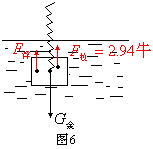
　　　 (3)根据力的平衡原理列方程，代入公式、数值，进行计算，得出结果。

　　　 例题中弹簧秤下面挂着的金属是研究对象。当金属块浸没在水中时，受到浮力、拉力、重力的作用。其受力示意图如图6所示。

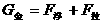
　　　 将公式、数值代入

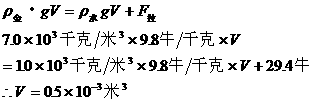
　　　 已知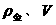，就可推导计算金属块的重力。

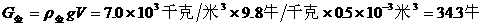
　　　 例5：一木块浮在水面上，露出水面的体积为32厘米³，把露出水面的部分截去后，原水下部分又有24厘米³体积露出水面，求：(1)木块的体积。(2)木块的密度。

　　　 分析与解：

　　　 审题确定研究对象所处状态，画出状态图分析研究对象受力情况画出示意图。

　　　 解法一：

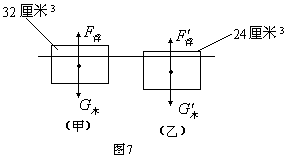
　　　 木块被截前后受力分别如图7(甲)(乙)所示。

　　　 其中(甲)图中

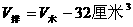，(乙)图中，

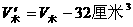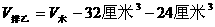
　　　 (甲)图中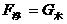

　　　 (乙)图中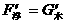

　　　 代入公式展开

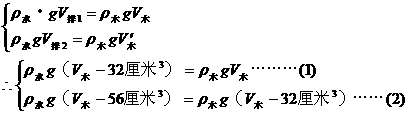
1、必须弄清楚的一些概念

　　　 (1)物重G与弹簧秤的示数

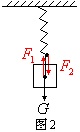
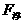　　　 弹簧秤的示数显示了，物体拉弹簧的力，或弹簧拉物体的力的大小，和是一对作用力和反作用力。在浮力问题中通常弹簧的示数，就给出了。如图2，物体在空气中静止，与二力平衡。如果物体浸在液体中静止，、、G三力平衡，此时。

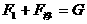　　　 (2)物重G与物体排开的液重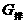

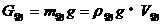
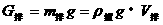　　　　　　　 当物体完全浸没，。

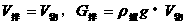　　　 (3)浸在(浸入)与浸没(没入)

　　　 浸在(浸入)是指物体一部分在液体中，或物体全部在液体中的两种情况。

　　　 浸没(没入)是指物体全部在液体中的一种情况。

　　　 (4)上浮、漂浮、悬浮

　　　 物体只受重力和浮力作用下，如果物体向上运动的状态叫做上浮；如果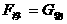，物体静止在液面上的状态叫做漂浮，如果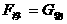物体没入液体中静止叫做悬浮。

　　　 (5)物体的密度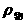与液体的密度。

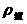　　　 (6)物体的体积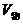，物体排开液体的体积，物体露出液面的体积。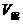

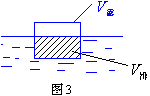
　　　 如图3所示，物体漂浮在液面上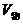，是物体的体积，是物体浸入液体中的体积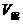，是物体露出液面的体积。所以=+。

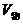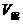2、潜水艇、气球、飞艇

　　　 潜水艇、气球、飞艇共同一处是可以上浮、下沉、悬浮，不同之处只是控制的方法不同。

　　　 潜水艇是利用改变自重，实现它的上浮和下潜。气球和飞艇的升空和下降，主要是靠改变它们所受浮力来实现的。

[典型应用]：