7. 如图所示，从倾角为θ的斜面上A点，以水平速度v₀抛出一个小球，不计空气阻力，它落到斜面上B点时所用的时间为(　　 )

6. 一个物体以初速度v₀水平抛出，落地时速度的大小为v，则运动时间为(　　 )

A. 　　　　B. 　　　C. 　　D.

5. 用跨过定滑轮的绳把湖中小船拉靠岸，如图，已知拉绳的速度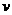保持不变，则船速(　　 )

A. 保持不变　　　 B. 逐渐增大

　 C. 逐渐减小　　　 D. 先增大后减小

4. 关于运动的合成与分解的说法中，正确的是(　　 )

A. 合运动的位移为分运动的位移的矢量和.

B. 合运动的速度一定比其中一个分速度大.

C. 合运动的时间为分运动时间之和.

D. 合运动的时间与各分运动时间相等.

3. 下列说法中正确的是(　　 )

　　 A. 物体在恒力作用下不可能做曲线运动

　　 B. 物体在变力作用下有可能做曲线运动

　　 C. 做曲线运动的物体，其速度方向与合外力方向不在同一直线上

　　 D. 物体在变力作用下不可能做直线运动

2. 自由下落的物体，当它落到全程一半和全程所用的时间之比是(　　 )

A. 1：2　 B. 2：1　 C. 　D.

1. 在忽略空气阻力的情况下，让一重一轻的两块石头从同一高度同时开始下落，则下述正确的说法是(　　 )

　　 A. 重的石块落得快，先着地

　　 B. 轻的石块落得快，先着地

　　 C. 在着地前的任一时刻，两石块具有相同的速度、相同的位移、相同的加速度

　　 D. 两块石头在下落这段时间内的平均速度相等

(三)人造地球卫星、宇宙速度

　 1. 卫星的绕行速度v

设地球和卫星的质量分别为m’和m，卫星到地心的距离为r，卫星的运行速度为v，由于卫星运动所需的向心力由万有引力提供，所以

由此可得：卫星绕地球运行的速度

　　 ①卫星与地心的距离r越大，则v越小。

②高轨道发射卫星比低轨道发射卫星困难。原因是高轨道发射卫星时火箭要克服地球对它的引力做更多的功。

　 2. 地球的同步卫星(通讯卫星)

　　 ①同步卫星：相对地面静止，跟地球自转同步的卫星叫做同步卫星，周期h，同步卫星又叫做通讯卫星。

　　 ②同步卫星必定位于赤道正上方，且离地高度h，运行速率v是惟一确定的。

设地球质量为，地球半径为R=6.4×10⁶m，卫星质量为m，根据牛顿第二定律有

设地球表面重力加速度g=9.8m/s²，则GM’=R²g

以上两式联立解得

同步卫星距地面的高度为

③同步卫星的运行方向与地球的自转方向相同。

3. 宇宙速度　

　　 (1)第一宇宙速度(环绕速度)：v₁=7.9km/s

　　 ①意义：它是人造卫星地面附近绕地球做匀速圆周运动所必须具备的速度。

　　 ②推导：

　　 方法一：卫星做圆周运动由万有引力提供向心力，根据牛顿第二定律得

方法二：由于卫星在地球附近运行时，卫星做圆周运动的向心力可看作由重力提供，根据牛顿第二定律得

　　 ③如果卫星的速度小于第一宇宙速度，卫星将落到地面而不能绕地球运转；等于这个速度卫星刚好能在地球表面附近做匀速圆周运动；如果大于7.9km/s，而小于11.2km/s，卫星将沿椭圆轨道绕地球运行，地心就成为椭圆轨道的一个焦点。

(2)第二宇宙速度(脱离速度)：

　　 ①意义：使卫星挣脱地球的引力束缚，成为绕太阳运行的人造行星的最小发射速度。

　　 ②如果人造天体的速度大于11.2km/s而小于16.7km/s，则它的运行轨道相对于太阳将是椭圆，太阳就成为该椭圆轨道的一个焦点。

　　 (3)第三宇宙速度(逃逸速度)：v₃=16.7km/s

①意义：使卫星挣脱太阳引力束缚的最小发射速度。

②如果人造天体具有这样的速度并沿着地球绕太阳的公转方向发射时，就可以摆脱地球和太阳引力的束缚而邀游太空了。

4. 人造卫星的发射速度和运行速度

　　 人造卫星的发射速度与运行速度是两个不同的概念

　　 (1)发射速度：

　　 所谓发射速度是指被发射物在地面附近离开发射装置时的初速度，并且一旦发射后就再无能量补充，被发射物仅依靠自己的初动能克服地球引力上升一定的高度，进入运动轨道。要发射一颗人造地球卫星，发射速度不能小于第一宇宙速度。若发射速度等于第一宇宙速度，卫星只能“贴着”地面近地运行。如果要使人造卫星在距地面较高的轨道上运行，就必须使发射速度大于第一宇宙速度。

　　 (2)运行速度：是指卫星在进入运行轨道后绕地球做匀速圆周运动的线速度。当卫星“贴着”地面运行时，运行速度等于第一宇宙速度。根据可知，人造卫星距地面越高(即轨道半径r越大)，运行速度越小。实际上，由于人造卫星的轨道半径都大于地球半径，所以卫星的实际运行速度一定小于发射速度。

　　 (3)人造卫星的发射速度与运行速度之间的大小关系是：

[典型例题]

例1. 跳伞员从350m高空离开直升飞机开始落下，最初未打开降落伞，自由下落一段距离后才打开降落伞，打开降落伞后以2m/s²的加速度匀减速下落，到达地面时速度为4m/s，求跳伞员自由下落的高度(g=10m/s²)。

解析：跳伞员从离开直升飞机到落地包括两个过程，即自由落体运动过程和匀减速直线运动过程，解题的关键是弄清这两个过程的联系。自由落体运动过程的末速度就是匀减速直线运动过程的初速度，两个过程的位移大小之和就等于直升飞机离地面的高度。

如图1，设自由下落的高度为h，自由下落末速度为v，则：

设匀减速直线运动过程的加速度大小为a=2m/s²，则

由(1)、(2)得：h=59m

.

例2. 质量为3kg的物体以30m/s的初速度做竖直上抛运动，忽略空气阻力，则7秒末物体速度多大？7秒内位移多大？

解析：针对竖直上抛运动可以看成两个过程来分析，也可以看成一个过程来分析，将初速度方向设为正方向，则

负号表示与正方向相反。

负号表示与正方向相反，即物体7秒末在抛出点的下方。

例3. 一船在静水中的速度为8m/s，要横渡水流速为6m/s、宽的河，下面说法正确的是(　　 )

A. 船能行驶到正对岸

B. 过河的最少时间为

　　 C. 过河的最短位移为80m

D. 船在最短时间内过河时，船对岸的速度为8m/s

若其它条件不变，水流速度增大到12m/s，则(　　 )

E. 船不能过河

F. 船不能行驶到正对岸

　　 G. 过河的最少时间为

H. 船在最短时间内过河时，船对岸的速度为m/s

解析：船能否行驶到正对岸，与船的静水速和水流速的大小关系有关，如图2所示，当这两个速度的合速度能垂直正对岸时，那么船就可以行驶到正对岸，因此当船的静水速大于水流速时才可能到正对岸，当然如果这样渡河位移最短，等于河宽。因此A、C正确。要想渡河时间最短，则要求垂直河岸的速度最大，当然最大就等于船的静水速度，此最短时间为河宽除以船的静水速度，因此B正确。船的实际速度为合速度也称为船对岸的速度，船在最短时间内过河时，(船的静水速8m/s，水流速6m/s)，所以D错误。

　　 当水流速增大到12m/s时，大于船的静水速8m/s，因此不可能到正对岸，但不是过不了河，因此E错误、F正确。水流的快慢不影响渡河的最短时间，只要船头正对对岸，即静水速垂直正对岸，过河时间最短，因此G正确，，H正确。

答案：A、B、C；F、G、H 。

例4. 如图3所示是一小环做平抛运动的闪光照片的一部分，其中A、B、C是小球在不同时刻在照片上的位置。图中背景方格的边长均为l=5cm，如果取g=10m/s²，则小球的初速度_______。

解析：设时间间隔为T

水平方向：　

例5. 如图4所示，用皮带相连的轮子，大轮半径R等于小轮半径的2倍，大轮上点A到转轴O的距离AO=R/2，B、C两点分别在大轮与小轮边缘上，当大轮带动小轮转动，而皮带不打滑时，A、B、C三点的角速度之比是多少？线速度之比是多少？

解析：当皮带不打滑时，皮带上各处的速度和转动轮边缘各点的线速度大小都相等

同一转动体上各点的角速度都相同

例6. 如图5所示，一个小球被绳子牵引在光滑水平的平板上以速度v做匀速圆周运动，其运动的半径为R=30cm，v=1.0m／s，现将牵引的绳子迅速放长20cm，使小球在更大半径的新轨道上做匀速圆周运动，求：

　(1)实现这一过渡所经历的时间；

　(2)在新轨道上做匀速圆周运动，求小球的旋转角速度。

解析：(1)注意“迅速放长20cm”这句话，如图6所示，小球将沿切线AB方向运动至B，在直角三角形OAB中，R=0.3m，R′=0.5m，，则d=0.4m，故过渡时间t为

　

　(2)小球刚运动到B点的瞬间速度v=1m/s，沿AB方向，在此瞬间细绳沿OB方向突然张紧，沿OB方向的分速度突然消失，球将以分速度做匀速圆周运动，由图中相似三角形关系可得

　

　

例7. 地球可视为球体，其自转周期为T，在它的两极处，用弹簧秤测得某物体重为P，在它的赤道上，用弹簧秤测得同一物体重为0.9P，地球的平均密度是多少？

解析：重力是由于地球对物体的吸引而产生的力，但是不能认为重力就是地球对物体的吸引力。严格地讲，只有在两极处，重力才等于地球对物体的万有引力；在地球的其他地方，重力都小于地球对物体的万有引力。由于重力与地球对物体的万有引力差别极小，所以通常近似视为重力等于地球对物体的万有引力。

设被测物体的质量为m，地球的质量为M，半径为R；在两极处时物体的重力等于地球对物体的万有引力。即：

在赤道上，因地球自转物体做匀速圆周运动，地球对物体的万有引力和弹簧秤对物体的拉力的合力提供向心力，根据牛顿第二定律有：

由以上两式解得地球的质量为：

根据数学知识可知地球的体积为

根据密度的定义式可得地球的平均密度为

例8. 在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才停下来。假设着陆器第一次落到火星表面弹起后，到达最高点时高度为h，速度方向是水平的，速度大小为v₀，求它第二次落到火星表面时速度的大小，计算时不计火星大气阻力。已知火星的一个卫星的圆轨道的半径为r，周期为T。火星可视为半径为r₀的均匀球体。

解析：以g′表示火星表面附近的重力加速度，M表示火星的质量，m表示火星的卫星的质量，m′表示火星表面处某一物体的质量，由万有引力定律和牛顿第二定律，有

设v表示着陆器第二次落到火星表面时的速度，它的竖直分量为v₁，水平分量仍为v₀，有

　　 由以上各式解得　 　　

[模拟试题]

第Ⅰ卷(选择题　 共48分)

(二)万有引力定律在天文学上的应用

　 1. 重力加速度g=G

　 2. 行星绕恒星、卫星绕行星做匀速圆周运动，万有引力充当向心力，根据万有引力定律和牛顿第二定律可知

　　 G=ma_n，又a_n=，则

　　 v=，，T=

　 3. 中心天体的质量M和密度ρ

　　 由G=m

可得质量M=，可见，此常数与中心天体的质量M有关

　　 当r=R，即近地卫星绕中心天体运行时，

根据天体表面的重力加速度和天体半径求天体质量

　 　

(一)万有引力定律

　 1. 表述：自然界中任何两个物体都是相互吸引的，引力的大小跟这两个物体的质量成正比，跟它们的距离的二次方成反比。

　 2. 公式表示：

　 3. 引力常量G：

　　 ①意义：它在数值上等于两个质量都是1kg的物体相距1m时的相互作用力。

②G的通常取值为G=6.67×10^－11N·m²/kg²

　 4. 适用条件

　　 ①万有引力定律只适用于质点间引力大小的计算。当两物体间的距离远远大于每个物体的尺寸时，物体可以看成质点，直接使用万有引力定律计算。

　　 ②当两物体是质量均匀分布的球体时，它们间的引力也可直接用公式计算，但式中的r是指两球心间的距离。

　　 ③当研究物体不能看成质点时，可以把物体假想分割成无数个质点，求出两个物体上每个质点与另一物体上所有质点的万有引力，然后求合力。(此方法仅提供一种思路)