
题目列表(包括答案和解析)
18.解答 设太阳的质量为M;地球的质量为m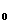 ,绕太阳公转的周期为T0,与太阳的距离为R
,绕太阳公转的周期为T0,与太阳的距离为R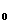 ,公转角速度为ω
,公转角速度为ω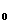 ;新行星的质量为m,绕太阳公转的周期为T,与太阳的距离为R,公转角速度为ω.根据万有引力定律和牛顿定律,得
;新行星的质量为m,绕太阳公转的周期为T,与太阳的距离为R,公转角速度为ω.根据万有引力定律和牛顿定律,得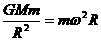 ①
①
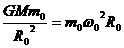 ② T=
② T=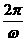 T0=
T0=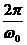 ③
③
由以上各式解 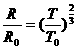 ④
④
将T=288年,T0=1年代入④,得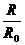 = 44(或
= 44(或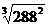 )
)
17. 解答:以g′表示火星表面附近的重力加速度,M表示火星的质量,m表示火星的卫星的质量,m′表示火星表面处某一物体的质量,由万有引力定律和牛顿第二定律,有
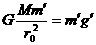 ①
①
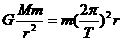 ②
②
设v表示着陆器第二次落到火星表面时的速度,它的竖直分量为v1,水平分量仍为v0,
有 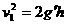 ③
③
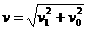 ④
④
由以上各式解得 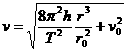 ⑤
⑤
16. 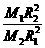 ;
;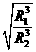
15.解答:由重量和质量的关系知: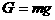
所以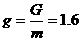 m/s2
m/s2
设:环绕该行星作近地飞行的卫星,其质量为m′,所以,应用牛顿第二定律有:
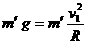 解得:
解得: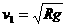
代入数值得第一宇宙速度: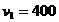 m/s
m/s
11. ;12.
;12.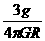 ;13.
;13.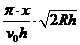 ;14.
;14.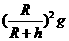
1.D 2.C 3.CD 4.D 5.A 6.AB 7.BC 8.C 9.C 10.A
18.据美联社2002年10月7日报道,天文学家在太阳系的9大行星之外,又发现了一颗比地球小得多的新行星,而且还测得它绕太阳公转的周期约为288年。若把它和地球绕太阳公转的轨道都看作圆,问它与太阳的距离约是地球与太阳距离的多少倍。(最后结果可用根式表示)
第七章 万有引力定律研究测试题( A )
17. 在勇气号火星探测器着陆的最后阶段,着陆器降落到火星表面上,再经过多次弹跳才停下来。假设着陆器第一次落到火星表面弹起后,到达最高点时高度为h,速度方向是水平的,速度大小为v0,求它第二次落到火星表面时速度的大小,计算时不计火星大气阻力。已知火星的一个卫星的圆轨道的半径为r,周期为T。火星可视为半径为r0的均匀球体。
16. 两个行星的质量分别是M1和M2,它们绕太阳运行的轨道半径分别等于R1和R2,假定它们只受到太阳的作用,求它们所受的向心力的比和运行周期的比各等于多少?
15.在某个半径为R=105m的行星表面,对于一个质量m=1kg的砝码,用弹簧称量,其重力的大小G=1.6N。请你计算该星球的第一宇宙速度v1是多大?(注:第一宇宙速度v1,也即近地、最大环绕速度;本题可以认为物体重力大小与其万有引力的大小相等。)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com