
题目列表(包括答案和解析)
6.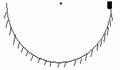 如图所示,一滑块从半圆形光滑轨道上端由静止开始滑下,当滑到最低点时,关于滑块动
能大小和对轨道最低点的压力,下列结论正确的是( )
如图所示,一滑块从半圆形光滑轨道上端由静止开始滑下,当滑到最低点时,关于滑块动
能大小和对轨道最低点的压力,下列结论正确的是( )
A、轨道半径越大,滑块动能越大,对轨道的压力越大
B、轨道半径越大,滑块动能越大,对轨道的压力与半径无关
C、轨道半径越大,滑块动能越大,对轨道的压力越小
D、轨道半径变化时,滑块动能、对轨道的正压力都不变
5. 如图所示,一斜面放在光滑的水平面上,一个小物体从斜面顶端无摩擦的自由滑下,则在下滑的过程中
( )
如图所示,一斜面放在光滑的水平面上,一个小物体从斜面顶端无摩擦的自由滑下,则在下滑的过程中
( )
A. 斜面对小物体的弹力做的功为零
B. 小物体的重力势能完全转化为小物体的动能
C. 小物体的机械能守恒
D. 小物体,斜面和地球组成的系统机械能守恒
4. 如图所示,质量为m和3m的小球A和B,系在长为L的细线两端,桌面水平光滑,高h(h<L),A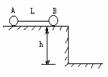 球无初速度从桌边滑下,落在沙地上静止不动,则B球离开桌边的速度为( )
球无初速度从桌边滑下,落在沙地上静止不动,则B球离开桌边的速度为( )
A.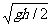 B.
B.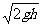
C.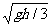 D.
D.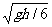
3. 从离地面高H米的阳台上以初速为v竖直向上抛出一质量为m的物体,它上升h米返回下落,最后落到地面上.则下列说法准确的是(不计空气阻力,取地面为重力势能零点)( )
A.物体在最高点的机械能为mg(H+h)
B.物体落到地面上时的机械能为mg(H+h)+ 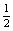 mv2
mv2
C. 物体落到地面上时的机械能为mgH+ 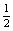 mv2
mv2
D.物体在运动过程中机械能保持不变
2.在离地高为H处以初速度v0竖直向下抛一个小球,若与地球碰撞的过程中无机械能损失,那么此球回跳的高度为( )
A、H+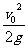 ; B、H-
; B、H-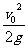 ; C、
; C、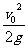 ; D、
; D、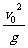 。
。
1. 关于关于机械能守恒,下列说法正确的是( )
A、做匀速直线运动的物体机械能守恒;
B、做匀变速直线运动的物体机械能守恒;
C、外力对物体做功为零时,物体的机械能守恒;
D、只有重力对物体做功,物体的机械能守恒。
课本题解
(3)在离地面某一高度初竖直向上抛出一小球,质量为1㎏,抛出的速度为4m/s,取抛出地面为零势能平面,最高点离参考平面的高度为多少?
解:根据机械能守恒由题意得
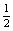 mv2=mgH代入数据得
mv2=mgH代入数据得
H= v2/2g=0.8m
巩固训练
5.利用机械能守恒定律解题的方法
①选取研究对象,确定物理过程。
②分析该物理过程是否满足机械能守恒定律。
③规定零势能参考平面,列式计算。
注意:列式时,要养成这样的习惯,等式作便是初状态的机械能而等式右边是末状态的机械能,这样有助于分析的条理性。
典型例题
[例1]在下列物理过程,机械能守恒的有 ( )
A、把一个物体竖直向上匀速提升的过程
B、人造卫星沿椭圆轨道绕地球运行的过程
C、汽车关闭油门后沿水平公路向前滑行的过程
D、从高处竖直下落的物体落在竖直的弹簧上,压缩弹簧的过程,对弹簧,物体和地球这一系统
[解答]向上匀速提升物体的过程中,除重力做功还有向上的外力做正功,物体的机械能增加;卫星运动只受重力作用,机械能守恒;汽车关闭发动机以后,要受到阻力的作用,机械能减小;物体压缩弹簧的过程中只有重力,弹簧的弹力做功,所以对整个系统总机械能守恒(而系统中物体或弹簧机械能不守恒)。
[点评]本题考查的是机械能守恒定律适合的条件.
[例2]如图所示,一轻质弹簧固定于O点,另一端系一重物,将重物从与悬挂点等高的地方无初速度释放,让其自由摆下,不及空气阻力,重物在摆向最低点的位置的过程中( )
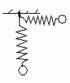 A.重物重力势能减小
A.重物重力势能减小
B.重物重力势能增大
C. 重物的机械能不变
D. 重物机械能减小
[解答] 物体从水平位置释放后,在向最低点运动时,物体的重力势能不断减小,动能不断增大.弹簧不断被拉长,弹性势能变大.所以物体减少的重力势能一部分转化为自身的动能,另一部分转化为弹簧的动能.对整个系统机械能守恒,而对重物来说,机械能减少.答案:AD
[点评]本题中的机械能守恒的对象是重物和弹簧组成的系统.而不是系统内部的单个物体.搞清研究对象是本题的关键.
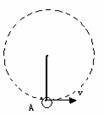
[例3]如图所示,小球用不可伸长的长为L的轻绳悬于O点,小球在最低点的速度必需为多大时,才能在竖直平面内做完整个圆周运动?
[解答]在整个过程中,小球只受到重力做功,绳中的拉力不做功.所以在整个过程中小球的机械能守恒. 设最低的速度为v,取最低点为零势能平面.则
 最低点的机械能E1=
最低点的机械能E1=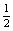 mv2
mv2
小球要在竖直平面内完成整个运周运动,在最高点的速度为起码为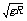
则在最高点的机械能E2=EK+EP=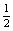 m(
m(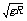 )2+mg×2R
)2+mg×2R
根据机械能守恒定律E1=E2 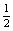 mv2=
mv2=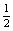 m(
m(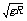 )2+mg×2R
)2+mg×2R
代入数据得v=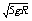
[点评]本题用机械能守恒定律,在解题过程中注意解题的方法和步骤。
方法总结:在用机械能守恒定律解题注意研究对象的选取,同时要注意零势能平面的选取,对同一个物理过程,所选取得平面一定要相同。
4.理解机械能守恒定律:
①从守恒的角度:物体运动过程中,初状态和末状态机械能相等E1=E2。
②从转化的角度:动能的增加等于势能的减少或动能的减少等于势能的增加。
即:ΔEK=-ΔEP
③从转移的角度:物体系一部分机械能的增加量等于另一部分机械能的减少量。
即:ΔA=-ΔEB.
3. 机械能守恒定律
①内容:一个系统,如果只有系统内部的重力和弹力做功,而其它内力或外力都不做功,则这个系统的动能与势能相互转化,而总的机械能保持不变。
②推导:设物体在运动过程中只存在重力做功,则有动能定理得WG=EK2-EK1 ,而WG=-(EP2-EP1),所以-(EP2-EP1)=EK2-EK1,即EK1+EP1=EK2+EP2.也可以写成E1=E2。
③成立条件:只有系统内部重力或弹力做功,其它力不做功。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com