15.如图4-1-13所示，矿井深100　 m，用每米质量为1 kg的钢索把质量为100 kg的机器从井底提到井口，至少应该做多少功？(机器可视为质点，g取10　 m/s²)

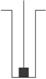
图4-1-13

解析：机器被提到井口时，绳子重心升高了50 m，其重力势能增加0.5×10⁵ J，机器重力势能增加1.0×10⁵ J，因此所做的功应等于绳子和机器重力势能增加量之和，即1.5×10⁵ J.

答案:1.5×10⁵ J

12.如图4-1-10所示，求质量为m的小球从位置A运动到位置B的过程中重力所做的功.

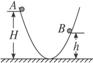
图4-1-10

解析：由于重力做功与通过的路径无关，只决定于物体的重力mg和物体初末位置的高度差，所以物体由A位置运动到B位置，虽然先运动到地面高度再回到B高度，但初末位置的高度差是H-h，那么重力做的功就是W＝mg(H-h).

答案:mg(H-h)

我综合　 我发展

10.为了测定一根轻弹簧压缩最短时能储存的弹性势能大小，可以将弹簧固定在一凹槽轨道的一端，并将轨道固定在水平桌面边缘上，如图4-1-9所示，用钢球将弹簧压缩至最短，而后突然释放，钢球将沿轨道飞出桌面.实验时：

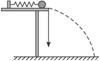
图4-1-9.

(1)需要测定的物理量有_________________.

(2)计算弹簧压缩最短时弹性势能的关系式是E_p=______________.

解析：小球被弹出后做平抛运动，弹簧被压缩时的弹性势能应等于小球做平抛运动的初动能.因此，可以测出小球离地面的竖直高度h、小球落地点的水平距离s，然后根据平抛运动的规律求出小球抛出时的初速度，即可求出弹簧被压缩后的弹性势能.

答案:(1)小球离地面的竖直高度h，小球落地点的水平距离s

(2)

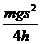
8.如图4-1-8所示，小球质量为m，大小不计，右边圆轨道半径为R，小球从h=3R处沿斜轨滑下后，又沿圆轨道滑到最高点P处，在这一过程中，重力对小球所做的功为_________，小球重力势能减少了___________.

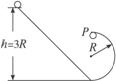
图4-1-8

解析：求重力对小球做的功，直接确定小球在竖直方向上的高度差，重力做正功mgR，则重力势能就减小mgR.

答案:mgR　 mgR

17.(经典回放)面积很大的水池，水深为H，水面上浮着一正方体木块.木块边长为a，密度为水的1/2，质量为m.开始时，木块静止，有一半没入水中，如图4-1-15 所示.现用力F将木块缓慢地压到池底.不计摩擦.求:

(1)从木块刚好完全没入水中到停在池底的过程中,池水势能的改变量;

(2)从开始到木块刚好完全没入水的过程中，力F所做的功.

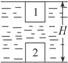
解析：(1)右图中，1和2分别表示木块在刚没入水中时和到达池底时的位置.木块从1位置移到2位置，相当于使同体积的水从2移到1，所以池水势能的改变量等于这部分水在位置1和在位置2的势能之差.因为木块密度为水的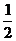，木块的质量为m,所以与木块同体积的水的质量为2m.故池水势能的改变量为

ΔE=2mg(H-a).

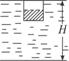
(2)因为水池面积很大，可忽略因木块压入水中所引起的水深变化.木块刚好完全没入水中时，右图中原来处于划斜线区域的水被排开，后果等效于使这部分水平铺于水面，这部分水的质量为m,其势能的改变量为

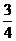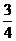ΔE_水=mgH-mg(H-a)=mga

木块势能的改变量为ΔE_木=mg(H-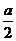)-mgH=-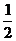mga

根据动能定理，力F所做的功为W=ΔE_水+ΔE_木=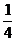mga.

答案:(1)2mg(H-a)　 (2)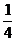mga

物理沪科版必修2：同步测控(4.1 势能的变化与机械功)(带解析)同步测控

我夯基　 我达标

16.如图4-1-14所示，一物体质量m＝2 kg，在倾角θ＝37°的斜面上的A点以初速度v₀＝3 m/s下滑.A点距弹簧上的挡板位置B的距离为AB＝4 m，当物体到达B后，将弹簧压缩到C点，最大压缩量为BC＝0.2 m，然后物体又被弹簧弹上去，弹到最高位置D点，D点距A点为AD＝3 m.求：物体跟斜面间的动摩擦因数.(g取10　 m/s²，弹簧及挡板质量不计)

图4-1-14

解析：此题看上去似乎很复杂，涉及重力、弹力、摩擦力做功的问题.其实认真分析一下就会发现，在物体从B→C又返回到B时，弹簧先做负功，又做了相等数量的正功.总功为零，即弹力功为零；而重力做功根据其特点，只考虑由A到D的高度差即可；摩擦力做功由于与路径有关，须认真计算物体在全程中的路程.可见，对不同性质的力做功要具体分析，才会既简化问题又避免发生错误.

利用动能定理,对A→B→C→D全过程列式：

W_总=mgs_AD·sinθ-f(s_AB+2s_BC+s_BD)=0-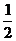mv₀²

f=μmgcosθ

两式联立可解得：μ=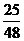≈0.52.

答案:0.52

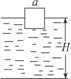
图4-1-15

15.如图4-1-13所示，矿井深100　 m，用每米质量为1 kg的钢索把质量为100 kg的机器从井底提到井口，至少应该做多少功？(机器可视为质点，g取10　 m/s²)

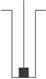
图4-1-13

解析：机器被提到井口时，绳子重心升高了50 m，其重力势能增加0.5×10⁵ J，机器重力势能增加1.0×10⁵ J，因此所做的功应等于绳子和机器重力势能增加量之和，即1.5×10⁵ J.

答案:1.5×10⁵ J

14.如图4-1-12所示，劲度系数为k₁的轻质弹簧两端分别与质量为m₁、m₂的物块1、2拴接，劲度系数为k₂的轻质弹簧上端与物块2拴接，下端压在桌面(不拴接)，整个系统处于平衡状态.现施力将物块1缓慢竖直上提，直到下面那个弹簧的下端刚好脱离桌面.在此过程中，物块2的重力势能增加了_________，物块1的重力势能增加了___________.

图4-1-12

解析：设原来两弹簧压缩量分别为x₁和x₂，由物体受力平衡知

x₁=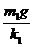,x₂=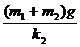

当施力将物块1缓慢上提至下面弹簧刚好脱离桌面时，下面的弹簧恢复原长，物块2升高的高度h₂=x₂，所以在此过程中，物块2的重力势能增加

ΔE_p2=m₂gh₂=m₂gx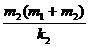₂=g²

此时，上面的弹簧受到拉伸，设其伸长量为x₁′，由物块2的平衡条件知，

x₁′=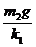

则物块1在这过程中升高的高度为

h₁=x₁+x₂+x₁′=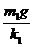++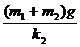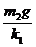=(m₁+m₂)(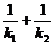)g.

所以，物块1的重力势能增加

ΔE_p1=m₁gh₁=m₁(m₁+m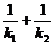₂)()g².

答案: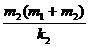g²　 m₁(m₁+m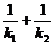₂)()g²

13.一质量均匀的不可伸长的绳索(重力不可忽略)，A、B两端固定在天花板上，如图4-1-11所示.今在最低点C施加一竖直向下的力将绳索拉至D点，在此过程中，绳索的重心位置将 …(　　 )

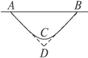
图4-1-11

A.逐渐升高　　　　 B.逐渐降低　　　　　 C.先降低后升高　　　　　 D.始终不变

解析：拉力对绳子做正功，根据动能定理可知，重力必定做负功，重心应逐渐升高.

答案:A

12.如图4-1-10所示，求质量为m的小球从位置A运动到位置B的过程中重力所做的功.

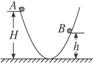
图4-1-10

解析：由于重力做功与通过的路径无关，只决定于物体的重力mg和物体初末位置的高度差，所以物体由A位置运动到B位置，虽然先运动到地面高度再回到B高度，但初末位置的高度差是H-h，那么重力做的功就是W＝mg(H-h).

答案:mg(H-h)

我综合　 我发展