

题目列表(包括答案和解析)
3.两颗人造地球卫星,都在圆形轨道上运行,它们的质量相等,轨道半径之比r1/r2=2.则它们的动能之比E1/E2等于( )
A.2 B.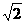 C.1/2 D.4
C.1/2 D.4
解析:根据G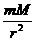 =m
=m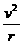 可得:卫星的动能E=
可得:卫星的动能E=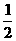
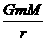 ,所以
,所以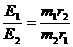 =
=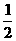 .
.
答案:C
17.(经典回放)某颗地球同步卫星正下方的地球表面上有一观察者,他用天文望远镜观察被太阳光照射的此卫星,试问,春分那天(太阳光直射赤道)在日落后的12小时内有多长时间该观察者看不见此卫星?已知地球半径为R,地球表面处的重力加速度为g,地球自转周期为T,不考虑大气对光的折射.
解析:设所求的时间为t,用m、M分别表示卫星和地球的质量,r表示卫星到地心的距离.
有G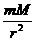 =mr(
=mr(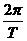 )2
)2
春分时,太阳光直射地球赤道,如图所示,图中圆E表示赤道,S表示卫星,A表示观察者,O表示地心.由图可看出当卫星S绕地心O转到图示位置以后(设地球自转是沿图中逆时针方向),其正下方的观察者将看不见它.据此再考虑到对称性,有
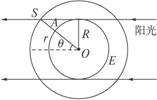
rsinθ=R
t=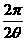 T
T

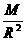 =g
=g
由以上各式可解得t=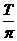 arcsin(
arcsin(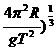 .
.
答案: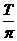 arcsin(
arcsin(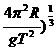
同步测控
我夯基 我达标
16.(经典回放)在勇气号火星探测器着陆的最后阶段,着陆器降落到火星表面上,再经过多次弹跳才停下来.假设着陆器第一次落到火星表面弹起后,到达最高点时高度为h,速度方向是水平的,速度大小为v0,求它第二次落到火星表面时速度的大小.计算时不计火星大气阻力,已知火星的一个卫星的圆轨道的半径为r,周期为T0.火星可视为半径为r0的均匀球体.
解析:以g′表示火星表面附近的重力加速度,M表示火星的质量,m表示火星的卫星的质量,m′表示火星表面处某一物体的质量,由万有引力定律和牛顿第二定律,有
G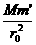 =m′g′
=m′g′
G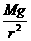 =m
=m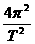 r
r
设v表示着陆器第二次落到火星表面时的速度,它的竖直分量为v1,水平分量仍为v0,有
v1=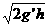
v=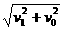
由以上各式解得
v=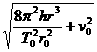 .
.
答案:v=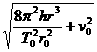
15.一艘宇宙飞船飞近某一不知名的行星,并进入靠近该行星表面的圆形轨道,宇航员进行预定的考察工作.宇航员能不能仅用一只表通过测定时间来测定该行星的密度?说明理由及推导过程.
答案:使宇宙飞船靠近行星表面做匀速圆周运动,设行星质量为M,宇宙飞船质量为m,行星半径为r,测出飞船运行周期为T.G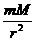 =mr(
=mr(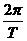 )2,所以M=
)2,所以M=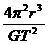 .又行星的体积V=
.又行星的体积V=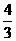 πr3,所以ρ=
πr3,所以ρ=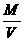 =
=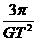 ,即宇航员只需测出T就能求出行星的密度.
,即宇航员只需测出T就能求出行星的密度.
14.探测器探测到土星外层上有一个环.为了判断它是土星的一部分还是土星的卫星群,可以测量环中各层的线速度v与该层到土星中心的距离R之间的关系来确定( )
A.若v∝R,则该环是土星的一部分
B.若v2∝R,则该环是土星的卫星群
C.若v∝1/R,则该环是土星的一部分
D.若v2∝1/R,则该环是土星的卫星群
解析:若为土星的一部分与土星为一整体,则它们的角速度与周期相同,根据v=ωr可知v∝R.若为卫星群,则万有引力为卫星提供向心力,由公式G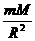 =m
=m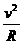 可得:v=
可得:v=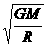 ,所以v2∝1/R.故A、D正确,B、C错误.
,所以v2∝1/R.故A、D正确,B、C错误.
答案:AD
13.某人在某一星球上以速度v竖直上抛一物体,经时间t落回抛出点,已知该星球的半径为R,若要在该星球上发射一颗靠近该星运转的人造星体,则该人造星体的速度大小为多少?
解析:星球表面的重力加速度g=
人造星体靠近该星球运转时:
mg=G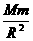 =m
=m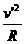 (M:星球质量,m:人造星体质量)
(M:星球质量,m:人造星体质量)
所以v′=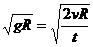 .
.
我综合 我发展
12.一艘宇宙飞船绕一个不知名的、半径为R的行星表面飞行,环绕一周飞行时间为T.求该行星的质量和平均密度.
解析:设宇宙飞船的质量为m,行星的质量为M.宇宙飞船围绕行星做匀速圆周运动.
G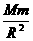 =m(
=m(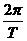 )2R
)2R
所以M=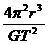
又v=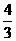 πR3
πR3
所以ρ=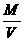 =
=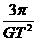 .
.
答案: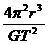
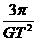
11.为了研究太阳演化进程,需知道目前太阳的质量M.已知地球半径R=6.4×106 m,地球质量m=6×1024 kg,日地中心的距离r=1.5×1011 m,取地球表面处的重力加速度g=10 m/s2,1年约为3.2×107 s,试估算目前太阳的质量M.(保留一位有效数字,引力常量未知)
解析:根据太阳对地球的引力提供地球绕太阳做圆周运动(近似处理)的向心力列出相关方程,再根据地球表面物体重力等于引力列出方程联立求解.
答案:设T为地球绕太阳运动的周期,则由万有引力定律和动力学知识得:G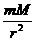 =mr(
=mr(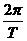 )2,对地球表面物体m′,又有
)2,对地球表面物体m′,又有
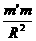 =m′g,由以上两式解得:M=
=m′g,由以上两式解得:M=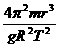 ,代入已知数据可得M=2×1030 kg.
,代入已知数据可得M=2×1030 kg.
10.(经典回放)据美联社2002年10月7日报道,天文学家在太阳系的八大行星之外,又发现了一颗比地球小得多的新行星,而且还测得它绕太阳公转的周期约为288年.若把它和地球绕太阳公转的轨道都看作圆,问它与太阳的距离约是地球与太阳距离的多少倍?(最后结果可用根式表示)
解析:新行星和地球绕太阳做圆周运动,万有引力提供向心力.
答案:设太阳质量为M,地球质量为m0,地球绕太阳运行的公转周期为T0,与太阳的距离为R0,由于万有引力提供向心力,则有:G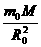 =m0R0(
=m0R0(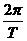 )2,对新行星同理可得:G
)2,对新行星同理可得:G =m′R′(
=m′R′(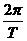 )2,由以上两式解得:
)2,由以上两式解得: ≈44.
≈44.
9.(经典回放)已知万有引力常量G,地球半径R,月球和地球之间的距离r,同步卫星距地面的高度h,月球绕地球的运转周期T1,地球的自转周期T2,地球表面的重力加速度g.某同学根据以上条件,提出一种估算地球质量M的方法:
同步卫星绕地球做圆周运动,由G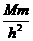 =m(
=m(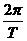 )2h得M=
)2h得M=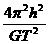 .
.
(1)请判断上面的结果是否正确,并说明理由.如不正确,请给出正确的解法和结果.
(2)请根据已知条件再提出两种估算地球质量的方法并解得结果.
解析:(1)不正确.应为G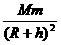 =m(
=m( )2(R+h),得M=
)2(R+h),得M=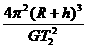 .
.
(2)由mg=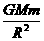 得M=
得M=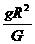 或由G
或由G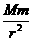 =m(
=m(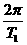 )2r得M=
)2r得M=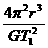 .
.
答案:见解析
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com