
题目列表(包括答案和解析)
12.月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天,试用开普勒定律计算出:在赤道平面内离地面多大高度,人造地球卫星可以随地球一起转动,就像停留在天空不动一样.(地球半径约为6.4×103 m)
解析:设人造地球卫星的轨道半径为R,周期为T.由于卫星在赤道平面内随地球一起转动,相对地球静止,所以,卫星绕地球转动的周期必然和地球自转的周期相同,即T=1 d.
设月球绕地球运动的轨道半径为R′,地球的半径为R0,则R′=60R0,
设月球绕地球运动的周期为T′,则T′=27 d.
由开普勒第三定律得
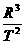 =
=
解得:R=R′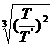 =60R0
=60R0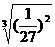 =6.67R0
=6.67R0
卫星在赤道平面内离地面的高度为
H=R-R0=5.67R0=5.67×6.4×103 km=3.63×104 km.
答案:3.63×104 km
10.目前的航天飞机的飞行轨道都是近地轨道,一般在地球上空300-700 km处飞行,绕地球飞行一周的时间为90 min左右.这样,航天飞机离的宇航员在24 h内见到日落日出的次数应为( )
A.0.38 B.1 C.2.7 D.16
解析:航天飞机绕行到地球向阳的区域,阳光能照射到它时为白昼,当飞到地球背阳的区域,阳光被地球挡住时就是黑夜.因航天飞机绕地球一周所需时间为90 min,而地球昼夜交替的周期是24×60 min,所以,航天飞机里的宇航员在绕行一周的时间内,看到日落日出的次数
n=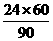 =16.
=16.
答案:D
7.某行星沿椭圆轨道运行,远日点离太阳的距离为a,近日点离太阳的距离为b,过远日点时行星的速率为vA,则过近日点时的速率为( )
A.vb=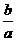 va
B.vb=
va
B.vb=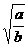 va
C.vb=
va
C.vb=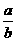 va D.vb=
va D.vb=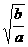 va
va
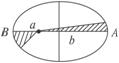
解析:如图所示,A、B分别为远日点、近日点,由开普勒第二定律,太阳和行星的连线在相等时间里扫过的面积相等,取足够短的时间Δt,则有
va·Δt·a=vb·Δt·b
所以vb=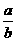 va.
va.
答案:C
5.人造地球卫星运行时,其轨道半径为月球轨道半径的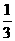 ,则此卫星运行周期是( )
,则此卫星运行周期是( )
A.1-4天 B.4-8天 C.8-16天 D.大于16天
解析:由人造地球卫星和月球均为地球的卫星,由开普勒第三定律可确定选项B正确.
答案:B
13.飞船沿半径为R的圆周绕地球运动,如图5-1-3所示,其周期为T,如果飞船要返回地面,可在轨道上某一点A处将速率降低到适当数值,从而使飞船沿着以地心为焦点的椭圆轨道运行,椭圆和地球表面相切于B点,设地球半径为R0,问飞船从A点返回到地面上B点所需时间为多少?

图5-1-3
解析:开普勒定律虽是对太阳行星系统而言的,但该定律也适合于地球卫星系统,飞船返回时是以地心为焦点的椭圆轨道运行,那么应用开普勒第三定律可求返回时间
飞船返回时间为椭圆运行周期T′的一半,而椭圆的长半轴为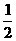 (R+R0),
(R+R0),
由开普勒第三定律可得
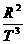 =
=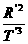
所以t=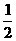 T′=
T′=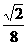 (1+
(1+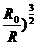 T.
T.
答案: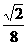 (1+
(1+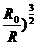 T
T
物理沪科版必修2:同步测控(5.1 从托勒密到开普勒)(带解析)同步测控
我夯基 我达标
12.月球环绕地球运动的轨道半径约为地球半径的60倍,运行周期约为27天,试用开普勒定律计算出:在赤道平面内离地面多大高度,人造地球卫星可以随地球一起转动,就像停留在天空不动一样.(地球半径约为6.4×103 m)
解析:设人造地球卫星的轨道半径为R,周期为T.由于卫星在赤道平面内随地球一起转动,相对地球静止,所以,卫星绕地球转动的周期必然和地球自转的周期相同,即T=1 d.
设月球绕地球运动的轨道半径为R′,地球的半径为R0,则R′=60R0,
设月球绕地球运动的周期为T′,则T′=27 d.
由开普勒第三定律得
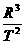 =
=
解得:R=R′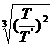 =60R0
=60R0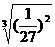 =6.67R0
=6.67R0
卫星在赤道平面内离地面的高度为
H=R-R0=5.67R0=5.67×6.4×103 km=3.63×104 km.
答案:3.63×104 km
11.有一行星,距太阳的平均距离是地球到太阳平均距离的8倍,则该行星绕太阳公转周期是多少年?
解析:地球绕太阳运行的周期为1年,由开普勒第三定律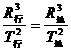 =恒量即可求出行星绕太阳运行的周期.
=恒量即可求出行星绕太阳运行的周期.
答案:根据开普勒第三定律: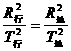 ,即
,即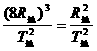 ,解得:T行=16
,解得:T行=16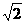 T地=22.6年.
T地=22.6年.
10.目前的航天飞机的飞行轨道都是近地轨道,一般在地球上空300-700 km处飞行,绕地球飞行一周的时间为90 min左右.这样,航天飞机离的宇航员在24 h内见到日落日出的次数应为( )
A.0.38 B.1 C.2.7 D.16
解析:航天飞机绕行到地球向阳的区域,阳光能照射到它时为白昼,当飞到地球背阳的区域,阳光被地球挡住时就是黑夜.因航天飞机绕地球一周所需时间为90 min,而地球昼夜交替的周期是24×60 min,所以,航天飞机里的宇航员在绕行一周的时间内,看到日落日出的次数
n=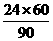 =16.
=16.
答案:D
9.地球公转运行的轨道半径R=1.49×1011 m,若把地球公转周期称为1年,那么土星运行的轨道半径R=1.43×1012 m,其公转周期为多长?
解析:地球和土星均为太阳的行星,对太阳系的所有行星,其运行轨道半径R和运行周期R均满足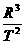 =k.
=k.
答案:根据行星的运动规律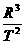 =k,有
=k,有 ,T′=29.7 T,即土星的公转周期为29.7年.
,T′=29.7 T,即土星的公转周期为29.7年.
我综合 我发展
8.两颗人造卫星A、B绕地球做圆周运动,周期之比为TA∶TB=1∶8,则轨道半径之比是多少?
解析:人造卫星做圆周运动的半径对应于椭圆轨道的半长轴,根据开普勒第三定律可得:
(rA∶rB)3=(TA∶TB)2=1∶64,即rA∶rB=1∶4.
答案:1∶4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com