1. 起重机竖直吊起质量为m的重物，匀加速上升的加速度是a，上升的高度是h，则起重机对货物所做的功为(　　 )

　　 A. mgh　　　　　　　　 B. mah　　　　　　　　　 C. mgh+mah　　　　 D. mgh－mah

2. 机械能守恒的条件

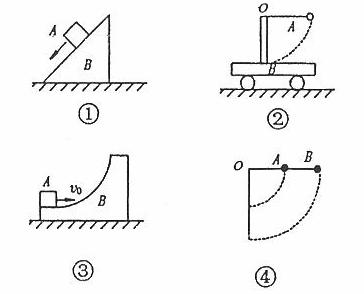
　　 “只有重力和弹力做功”这一条件可理解为包含下列三种情况：①只受重力或弹力；②除重力和弹力外，其他力不做功；③除重力和弹力，其他力做功的代数和为零。如汽车爬坡时，若牵引力和阻力相等则属于这种情况。这里的“其他力”包括外力和内力，如炸弹爆炸、气体膨胀等均属于内力做功造成了机械能的改变。在具体的题目中，判断机械能是否守恒至关重要，一定要认真分析，千万不能想当然。例如，如图所示的各种情况下，均不计一切摩擦，在判断A、B机械能是否守恒时，不少同学仅凭以往做题所得来的片面的感性认识，认为物体沿斜面和曲面滑动时，支持力不做功，杆对小球的作用力在球摆动过程中对球也不做功，所以下列各种情况中，物体A的机械能均守恒。仔细分析不难发现，这四种情况下，物体A所受的支持力或杆的拉力对A均做负功，A的机械能减少。而A和B构成的系统却满足守恒条件，在运动的过程中机械能守恒。

[典型例题]

　 例1. 一个质量为m的木块，从半径为R、质量为M的1/4光滑圆槽顶端由静止滑下。在槽被固定和可沿着光滑平面自由滑动两种情况下，如图所示，木块从槽口滑出时的速度大小之比为多少？

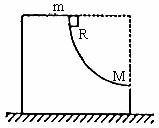
　　 解析：圆槽固定时，木块下滑过程中只有重力做功，木块的机械能守恒。木块在最高处的势能全部转化为滑出槽口时的动能。由：

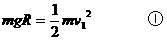
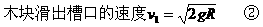
　　 圆槽可动时，当木块开始下滑到脱离槽口的过程中，对木块和槽所组成的系统，水平方向不受外力，水平方向动量守恒。

　　 设木块滑出槽口时的速度为v₂，槽的速度为u，则：

　　 mv₂+Mu＝0　　　　　　　　　　　 ③

　　 又木块下滑时，只有重力做功，机械能守恒，木块在最高处的势能转化为木块滑出槽口时的动能和圆槽的动能，即：

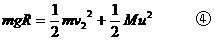
　　 联立③④两式解得木块滑出槽口的速度：

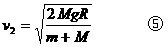
　　 因此，两种情况下滑出槽口的速度之比：

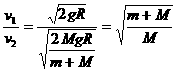
　 例2. 如图所示，在光滑水平面上有两辆车处于静止状态，其上分别站有甲、乙两个小孩，每辆车和小孩的总质量均为M，甲车上的小孩拿着一质量为m的球。现小孩甲将球抛给乙，乙接住后又抛回给甲，如此重复多次，最后球又回到了甲的手中，求甲、乙两车最后的速率之比。

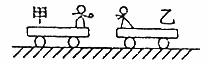
　　 解析：此题若先以甲车及其上的小孩和球为研究对象，应用动量守恒定律列出方程，再以乙车、小孩乙及球为研究对象同样列方程，如此这样分析下去，将非常繁锁。可见，这样选取研究对象显然是不好的。

　　 因为在抛球的过程中，只有两车、两个小孩和球组成的系统之间发生相互作用，因此可以两车、两小孩及球组成的系统为研究对象，以第一次小孩甲抛球时为初态，以最后小孩甲接住球为末态进行研究。因系统在水平方向不受外力，故系统动量守恒。初态系统的总动量为零；末态甲车、小孩及球的总动量为(M+m)v_甲，乙车及其上小孩的总动量为mv_乙，设甲车的运动方向为正，则据动量守恒定律便可解得。

　　 解：以两车、两小孩及球组成的系统为研究对象，选最后甲车速度为正方向，设最后甲、乙两车速度分别为v_甲、v_乙，自始至终系统动量守恒。

　　 对于系统的初、末状态由动量守恒得：

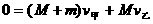
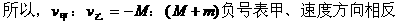
　　 甲、乙速率之比为M：(M+m)

　　 点评：

　　 ①从本题的求解过程不难看出，研究对象的选取和研究过程的确定对问题的顺利求解，起着至关重要的作用。

　　 ②本题的结果表明，无论球在两车之间抛多少次，两车的速率之比总为一定值。

　 例3. 如图，质量为0.5kg、长1.2m的金属盒AB，放在水平桌面上，它与桌面间动摩擦因数μ＝0.125。在盒内右端B处放着质量也为0.5kg、半径为0.1m的小球，球与盒间无摩擦。若在A端给盒以水平向右的冲量1.5N·s，设盒在运动中与球碰撞时间极短，且无能量损失，求：

　　 (1)盒从开始运动到完全停止所通过的路程是多少？

　　 (2)盒从开始运动到完全停止所经过的时间是多少？

　　 解析：(1)盒的初速度：

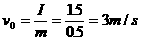
　　 盒从开始运动到完全停止的过程中，盒的初动能全部转化为因摩擦所产生的内能，所以：

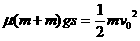
　　 所以盒通过路程为：

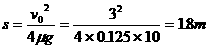
　　 (2)从盒开始运动到第一次碰撞的t₁时间内，球静止，盒减速运动，对盒有：

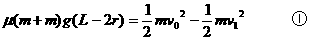
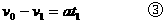
　　 由①②③得：t₁＝0.4s，v₁＝2m/s

　　 球与盒碰撞后二者交换速度，球再经时间t₂与盒第二次碰撞。所以：

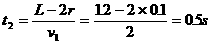
　　 二者碰后再次交换速度，盒再运动时间t₃停下，所以：at₃＝v₁

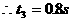
　　 t₃时间内盒子位移：

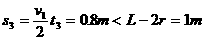
　　 所以盒子至停止运动不再和球发生碰撞，因此盒从开始运动到停下所用总时间：

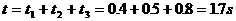
　 例4. 滑雪者从A点由静止沿斜面滑下，经一平台后水平飞离B点，地面上紧靠平台有一个水平台阶，空间几何尺度如图所示，斜面、平台与滑雪板之间的动摩擦因数为μ。假设滑雪者由斜面底端进入平台后立即沿水平方向运动，且速度大小不变。求：

　　 (1)滑雪者离开B点时的速度大小；

　　 (2)滑雪者从B点开始做平抛运动的水平距离s。

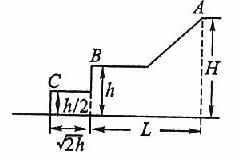
　　 解析：(1)设滑雪者质量为m，斜面与水平面夹角为θ，滑雪者滑行过程中克服摩擦力做功

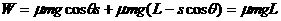
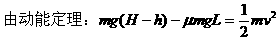
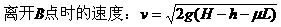
　　 (2)设滑雪者离开B点后落在台阶上

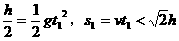
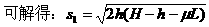
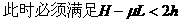
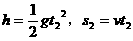
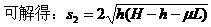
[模拟试题]

　　 如果说动量定理和动能定理研究对象仅限于单个物体的话，那么动量守恒定律和机械能守恒定律的研究对象则一定是由多个物体所构成的系统。二者的数学表达式常用形式分别为

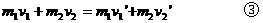
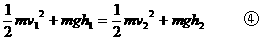
　　 在应用两个守恒定律解题时首先要注意系统的确定和守恒条件的确定。两个守恒定律的条件含义是完全不同的，解题时千万不能混为一谈。

1. 动量守恒的条件

　　 ①动量守恒定律的条件是系统不受外力的作用，但是实际上，根本不受外力作用的系统是不存在的，只要系统受的合外力为零，那么该系统就将严格遵循动量守恒定律，因为“合外力为零”与“不受外力作用”在对系统运动状态的变化上所产生的效果是相同的。

　　 ②在实际情况中，合外力为零的系统也是很少遇到的，因此在解决实际问题时，如果系统内部的相互作用力(即内力)远比它们所受的外力大(例如相互作用时间极短的碰撞类问题就是如此)就可忽略外力的作用，应用动量守恒定律去处理。

　　 ③动量守恒定律表示的是物理量之间的矢量关系，所以若系统所受的合外力并不为零，但合外力在某个方向上分量为零时，那么尽管系统的总动量不守恒，但总动量在该方向上的分量却是守恒的，例如平抛或斜抛出去的物体，它们只在竖直方向上受到外力，而水平方向上不受外力作用，因此尽管该物体在飞行的过程中总动量不守恒但在水平方向上动量却是守恒的。

　　 动量和动能是从不同角度描述物体运动状态的物理量。动量是矢量，而动能是标量；物体动量的变化用外力的冲量来量度，而动能的变化则用外力的功来量度。动量定理和动能定理的公式分别为：

　　 Ft＝mv₂－mv₁　　　　　　　　　　　　　　 ①

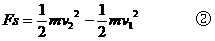
　　 虽然两个公式分别为矢量式和标量式，但不难看出二者仍有很多相同的地方。首先两个公式的形式是相似的；其次式中的v₁、v₂和s均应相对于同一惯性系；再者合外力的冲量Ft与合外力的功Fs在求解方法上也具有相似性，即可以先求合力F再求它的冲量或功，也可以先求各分力的冲量和功再合成。

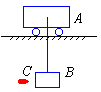
16、如图，小车A的质量为3kg，原来静止于光滑的水平轨道上，小车的前侧有一钉子，用长为1米的细线(不可伸长)悬挂一个质量为2kg的物体B，现有一颗质量为10g的子弹C，以600m/s的水平速度v₀射穿B后，速度变为，试求(1)子弹射穿物体后物体的速度是多少？(2)物体B向右摆动的最大高度。

15、如图所示，小球A从半径为R=0.8米的1/4光滑圆弧轨道的上端点以v0=3米/秒的初速度开始滑下，到达光滑水平面上以后，与静止于该水平面上的钢块B发生碰撞，碰撞后小球A被反向弹回，沿原路进入轨道运动恰能上升到它下滑时的出发点(此时速度为零)。设A、B碰撞机械能不损失，求A和B的质量之比是多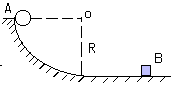少？　

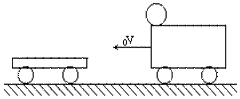
14、平直的轨道上有一节车厢，车厢以12m/s的速度做匀速直线运动，某时刻与一质量为其一半的静止的平板车挂接时，车厢顶边缘上一个小钢球向前滚出，如图所示，平板车与车厢顶高度差为1.8m，设平板车足够长，求钢球落在平板车上何处？(g取10m/s²)

13、一质量为30千克的小孩，以8米/秒的速度水平跑动中，从后面跑到一辆原来静止在水平面上的小车上并与小车保持相对静止。已知小车质量是10千克，小车与地面摩擦忽略不计。则小孩对小车的冲量大小为；小孩对小车所做的功为多少。

12、A和B两物体的质量分别为 mA 和 mB ，它们以相同的初动量开始沿同一水平面滑动。(1)若水平面对两物体的阻力相同，则它们滑动的距离 SA 与 SB 之比为_________。

(2)若水平面对两物体的滑动摩擦系数相同，则它们滑动的距离 SA 与 SB 之比为_____。