
题目列表(包括答案和解析)
2.关于式子U/I=R的物理意义,下面正确的叙述应是 ( BCD )
A.R与加在它两端的电压成正比,与通过它的电流成反比
B.通过R的电流跟加在R两端的电压成正比
C.对同一导体,在不计温度影响时,比值U/I总是一个恒量R(导体中间不含电源)
D.R可以用上式测量
1.关于导体和绝缘体的如下说法,其中正确是( ABC )
A.超导体对电流的阻碍作用等于零 B.自由电子通过导体时,仍受阻碍
C.绝缘体接在电路中,仍有极微小电流通过 D.绝缘体内一个自由电子也没有
12.如图43-20(a)所示,两根平行金属棒与两金属弹簧构成回路。已知棒长为L,质量为m,只能作左右对称的运动,边缘效应可以忽略。已知弹簧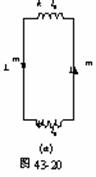 的劲度系数为K,原长为L0(L0«L),设以某种方式使回路有恒定的电流I,设电磁感应可以忽略。试求两棒围绕平衡位置作小振动的周期。
的劲度系数为K,原长为L0(L0«L),设以某种方式使回路有恒定的电流I,设电磁感应可以忽略。试求两棒围绕平衡位置作小振动的周期。
解:两棒中通有等值反向的电流,彼此间有斥力作用。当弹簧伸缩时又有弹力作用。先确定两棒的平衡位置。设平衡时,弹簧伸长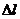 ,弹簧长度为
,弹簧长度为 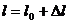
两棒所受弹力
安培力 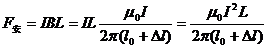
故平衡条件为: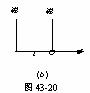
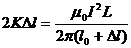 (1)
(1)
即 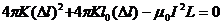
解出正根 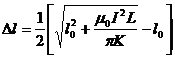
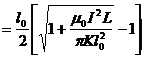 (2)
(2)
故平衡时两棒距离为
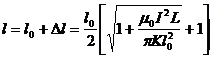 (3)
(3)
取 轴如图43-20(b),原点O设在右棒的平衡位置。设右棒向右偏离小量
轴如图43-20(b),原点O设在右棒的平衡位置。设右棒向右偏离小量 ,同时左棒向左偏离小量
,同时左棒向左偏离小量 ,即当两棒相距(
,即当两棒相距( )时,右棒受力为
)时,右棒受力为
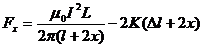
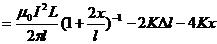

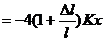
令 
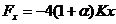
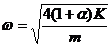
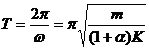
而 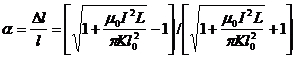
11.如图43-191所示,电子源每秒钟发射2.5×1013个电子,以υ0=8×106m/s速度穿过P板上的A孔,从MN两平行板正中央进入,速度方向平行于板且垂直于两板间的匀强磁场,已知MN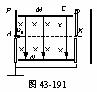 两板有恒定不变的电势差UMN=80V,板间距离d=1×10-3m,电子在MN间做匀速直线运动后通过小孔K进入的由CD两平行板组成的已充电的电容器中,已知电容C=8×10-8F,电子击中D板后被D板吸收,设时刻t1=0时,D板电势比C板高818V,在时刻t2=T,开始出现电子打中M板,已知电子m=9.1×10-31kg,q=1.6×10-19C,电子从A到D的运动时间不计,C、P两板都接地,电子间忽略碰撞与斥力,求:
两板有恒定不变的电势差UMN=80V,板间距离d=1×10-3m,电子在MN间做匀速直线运动后通过小孔K进入的由CD两平行板组成的已充电的电容器中,已知电容C=8×10-8F,电子击中D板后被D板吸收,设时刻t1=0时,D板电势比C板高818V,在时刻t2=T,开始出现电子打中M板,已知电子m=9.1×10-31kg,q=1.6×10-19C,电子从A到D的运动时间不计,C、P两板都接地,电子间忽略碰撞与斥力,求:
(1)MN之间匀强磁场的磁感应强度。
(2)时间T,以及电子打到M板上时,每个电子的动能(以eV为单位)。
(3)在时刻t3=-3/5T,打到D板上的电子流的功率。
解:(1)开始一段时间电子能在MN之间做匀速直线运动,说明
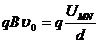 ,
,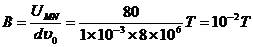
(2)开始时 ,
, 一直为零,随着D板吸收电子,电势降低,降到比零还要低,CD之间的电场力才会对电子做负功。在MN间匀速直线运动的电子具有动能为
一直为零,随着D板吸收电子,电势降低,降到比零还要低,CD之间的电场力才会对电子做负功。在MN间匀速直线运动的电子具有动能为
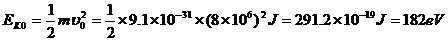
当D板电势降到-182V时,电子被D板反弹,从C板K孔向左射出,在复合场中受电场力与磁场力作用方向都向上,故电子向M板汇聚。CD两板间电压从D比C高818V到D比C低182V,共变化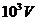 ,这段时间被D板吸收的电子总电量为
,这段时间被D板吸收的电子总电量为
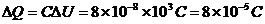
每秒钟吸收电子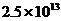 个,所以时间
个,所以时间

打中M板的电子被MN之间的电场力做了正功

(3) ,CD间电压变化为
,CD间电压变化为
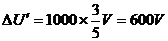
此时的电势仍是D板比C板高218V,CD之间的电场力对击中D板的电子做正功,每个电子击中D板时的动能为

电子流的功率

10. 如图43-129所示,一对竖直放置的平行金属板长为L,板间距离为d,板间电压为U。板间加一个与电场方向垂直的指向纸面向里的水平匀强磁场,磁感应强度为B,有一个质量为m、带正电的油滴,由离极板的上端点某高处的M点自由下落,通过两板上端连线中点N进入场区。已知油滴经过N点时在水平方向受力平衡,油滴通过场区后贴着正极板的下端点D处离开。求:
如图43-129所示,一对竖直放置的平行金属板长为L,板间距离为d,板间电压为U。板间加一个与电场方向垂直的指向纸面向里的水平匀强磁场,磁感应强度为B,有一个质量为m、带正电的油滴,由离极板的上端点某高处的M点自由下落,通过两板上端连线中点N进入场区。已知油滴经过N点时在水平方向受力平衡,油滴通过场区后贴着正极板的下端点D处离开。求:
(1)M点到N点的高度h多大?
(2)油滴在D点时的速度多大?
解:油滴经过N点时在水平方向受力平衡,说明它受到的电场力与洛伦兹力大小相等方向相反,从洛伦兹力能表示出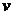 ,再由自由下落求出h。从N到D点,在场区中,随着油滴速度的变化,不再是直线运动而是较复杂的曲线运动,只能用功能关系求油滴在D点的速度。
,再由自由下落求出h。从N到D点,在场区中,随着油滴速度的变化,不再是直线运动而是较复杂的曲线运动,只能用功能关系求油滴在D点的速度。
(1)在N点,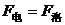
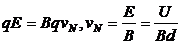 (1)
(1)
从M到N,机械能守恒
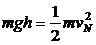 (2)
(2)
由(1)(2)得
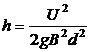 (3)
(3)
(2)从M到D的过程中,重力做功 ,电场力做功
,电场力做功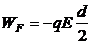 ,洛伦兹力不做功。
,洛伦兹力不做功。
根据动能定理 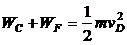
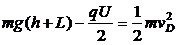
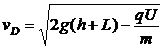 (4)
(4)
(3)代入(4)得
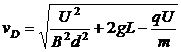
9.如图43-146(a)所示,一窄束单能氩离子通过一扇形匀强磁场,此束射线的轴在进、出磁场的时离子束的轴线都与场的边界垂直。求质量数为m1=36和m2=40的氩同位素束的发散角,已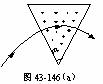 知ψ=60º。
知ψ=60º。
解:因为 ,而
,而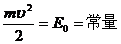 ,故不同质量离子的回转半径
,故不同质量离子的回转半径
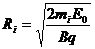
参见图43-146(b)在三角形 有
有
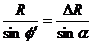
(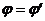 ,由于
,由于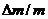 很小,可知角α很小,点D和
很小,可知角α很小,点D和 实际上几乎重合。)
实际上几乎重合。)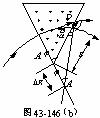
因此发散角
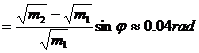
8. 如图43-110(a)所示,在x轴上方有垂直于xy平面向里的匀强磁场,磁感应强度为B;在x轴下方有沿y轴负方向的匀强电场,场强为E。一质量为m,电量为-q的粒子从坐标原点O沿着y轴正方向射出。射出之后,第三次到达x轴时,它与点O的距离为L。求此粒子射出时的速度υ和运动的总路程s(重力不计)。
如图43-110(a)所示,在x轴上方有垂直于xy平面向里的匀强磁场,磁感应强度为B;在x轴下方有沿y轴负方向的匀强电场,场强为E。一质量为m,电量为-q的粒子从坐标原点O沿着y轴正方向射出。射出之后,第三次到达x轴时,它与点O的距离为L。求此粒子射出时的速度υ和运动的总路程s(重力不计)。
解:粒子运动路线如图43-110(b)所示有
L=4R (1)
粒子初速度为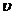 ,则有
,则有 
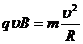 (2)
(2)
由(1)、(2)式要算得
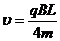 (3)
(3)
由 (1)、(2)、(3)、(4)、(5)、(6)式,得
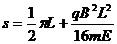
说明:粒子进入磁场在洛仑兹力作用下做匀速圆周运动,经过半圆周后,沿电场线方向进入电场,在电场力作用下做匀变速直线运动,最后又原路返回进入磁场,又重复以上运动。
3、液滴分裂成两个大小相同的液滴后,由于第一个液滴仍做圆周运动,由此,可知它所受的电场力与重力仍然平衡,故两个液滴不仅质量相等,而且其所带电量也相等又由于第一个液滴的轨道半径为R1=3R,并设其速度为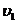 ,根据(3)式,同理可得其速度大小为
,根据(3)式,同理可得其速度大小为
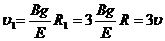 (4)
(4)
其绕行方向与原来液滴的绕行方向相同。
设分裂后第二个液滴的速度为 ,由动量守恒定律,得
,由动量守恒定律,得
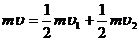
将(4)式代入上式得
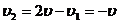
上式说明第二个液滴在A点的速度与原液滴速度大小相等,方向相反,即它仍在原运动平面内以 R为半径作匀速圆周运动,但该圆的最高点为A,绕行方向也是顺时针的。
2、因液滴做圆周运动,故知重力mg与电场力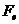 ,平衡,且磁场力
,平衡,且磁场力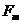 是液滴作圆周运动的向心力,即
是液滴作圆周运动的向心力,即
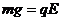 (1)
(1)
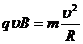 (2)
(2)
解(1)与(2)式得
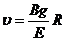 (3)
(3)
由于重力与电场力平衡,即电场力与电场强方向相反,故可以判断液滴带负电荷。在A点,它所受磁场作用力向上,电流方向应为向右,负电荷的绕行方向应为顺时针方向。
1、液滴受重力为mg、电场力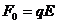 三个力作用(图43-80(b))。
三个力作用(图43-80(b))。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com