6. 波的干涉和衍射

[典型例题]

　 例1. 弹簧振子B的质量为M，弹簧的劲度系数为k，在B上面放一质量为m的木块A，使A和B一起在光滑水平面上做简谐运动，如图所示。振动过程中，A与B之间无相对运动，当它们离开平衡位置的位移为x时，A与B间的摩擦力大小为(　　 )

　　 精析：木块A作简谐运动时，由题意和牛顿第二定律可得：

　　 将木块A和振子B一起为研究对象，它们作简谐运动的回复力为弹簧的弹力所提供，应有

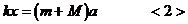
　　 由<1>式和<2>式可得：

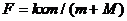
　 　答案：C

　　 说明：本题是讨论由静摩擦力提供A物体作简谐运动回复力的问题。这里特别要注意到当两物体达到最大位移时，振动时的加速度最大，A、B两个物体之间的静摩擦力是它们振动过程中的最大静摩擦力F_m'，但不一定是A、B两物体之间的最大静摩擦力F_m，这两者之间的关系是F_m≥F_m'。

　 例2. 某弹簧振子的固有频率为2.5 Hz，将弹簧振子从平衡位置拉开4 cm后放开，同时开始计时，则有t＝1.55s时(　　 )

　　 A. 振子正在做加速度减小的加速运动

　　 B. 振子正在做加速度增大的减速运动

　　 C. 振子的速度方向沿x轴正方向

　　 D. 振子的位移一定大于2 cm

　 　精析：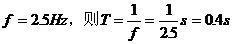

　　 根据简谐振动周期性的特点知：

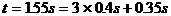
　　 振子在t＝1.2s时的运动状态与t＝0时相同，则t＝1.55s时的状态与t＝0.35s时的振动状态相同。作出振子的简谐运动图像如图所示，t＝0.35s时，对应于图线上的P点，振子此时正在向最大正位移处运动，加速度正在增大，速度正在减小，速度方向为正方向，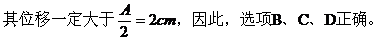

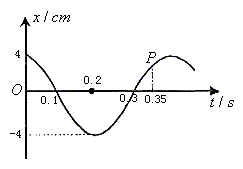
　　 振动的往复性是振动的最大特点。每经过一个周期，质点的运动状态恢复。所以，没有必要将振子在1.55s内的简谐运动的图像都做出来，只要观察振子在一个周期内的运动情况，以后的运动情况可顺推出来。

　 例3. 水平轨道AB，在B点处与半径R＝300m的光滑弧形轨道BC相切，一个质量为M＝0.99kg的木块静止于B处。现有一颗质量为m＝10g的子弹以v₀＝500m/s的水平速度从左边射入木块且未穿出，如图所示。已知木块与该水平轨道AB的动摩擦因数μ＝0.5(cos5°＝0.996，g取10m/s²)。试求：子弹射入木块后，木块需经多长时间停止？

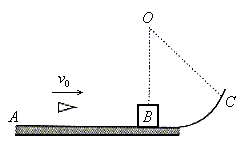
　 　精析：该题所描述的物理过程可划分为三个阶段：第一阶段为子弹与木块发生碰撞获得共同速度；第二阶段为子弹与木块一起在光滑圆弧形轨道上运动；第三阶段为子弹与木块又从B点开始在水平面AB上做匀减速运动。

　　 要求子弹射入木块后木块的运动时间，关键是第二个阶段所经历时间的计算，只有子弹与木块在BC面运动的幅度较小，才可将该阶段的运动看成等效单摆的运动，现估算如下：

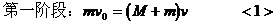
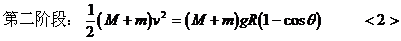
　　 由<1>式得：v＝5m/s

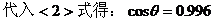
　　 与本题条件比较可知θ＝5°，故子弹与木块在BC面上的一个往返时间为等效单摆

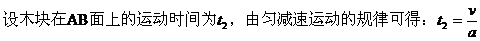
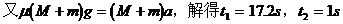
　　 故从子弹射入木块到它们停止共需经历18.2s。

　 　说明：一切在竖直平面放置的光滑圆弧形内轨道上的小幅度运动(运动范围远小于圆弧半径，运动过程中所对应的圆心角小于5°)，都可以等效为单摆模型，其等效摆长即

　 例4. 如图所示为沿水平方向的介质中的部分质点，每相邻两质点间距离相等，其中O为波源。设波源的振动周期为T，自波源通过平衡位置竖直向下振动时开始计时，经过T/4，质点1开始起振，则下列关于各质点的振动和介质中的波的说法中错误的是(　　 )

　　 A. 介质中所有质点的起振方向都是竖直向下的，且图中质点9起振最晚

　　 B. 图中所画出的质点起振时间都是相同的，起振的位置和起振的方向是不同的

　　 C. 图中质点8的振动完全重复质点7的振动，只是质点8振动时，通过平衡位置或最大位移的时间总是比质点7通过相同位置时落后T/4

　　 D. 只要图中所有质点都已振动了，质点1与质点9的振动步调就完全一致，但如果质点1发生的是第100次振动，则质点9发生的就是第98次振动

　 　精析：由波的形成原理可知，介质中的质点总是重复波源的振动形式，起振方向相同，但振动开始的时间不同，后面的质点总是落后于前面的质点，故A正确，B错；从题中可知，质点7是质点8的前质点，7、8质点间的振动步调相差T/4，故C正确；质点9比质点1晚2T开始起振，一旦质点9起振后，1、9振动步调就完全一致，故D正确。

　 　答案：B

　 例5. 如图所示，是一列横波在某一时刻的波形图，波沿x轴正向传播，则

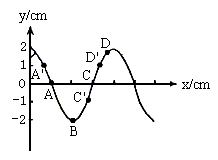
　　 (1)A点的振动方向是_______________，C点的振动方向是_______________，D点的振动方向是_______________。

　　 (2)再经T/2质点A通过的路程是__________cm，质点C的位移是__________cm。

　 　精析：微平移法：(1)波沿x轴正向传播，波源在左方，则在A点的左方附近找一点A'，见图。A'在A上方，故A向上运动。

　　 同理在C左方附近找一点C'，见图。C'在C下方，故C向下运动，同理知D向下运动。

　　 (2)质点A在T/2时间内振动了1/2个全振动，通过路程s＝2A＝2×2cm＝4cm，而要确定点C的位移，应先确定其运动方向，因C向下运动，经T/2，其刚好回到原来的地方，故其位移是0。

　　 答案：向上，向下，向下，4，0

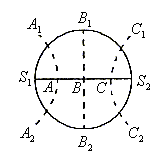
　 例6. 如图所示，在同一均匀媒质中有S₁、S₂两个波源，这两个波源的频率、振动方向均相同，且振动的步调完全一致，S₁、S₂之间相距两个波长，B点为S₁、S₂连线的中点，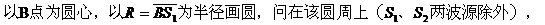

共有几个振动加强点？

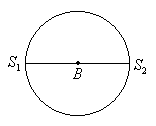
　 　精析：首先让我们分析S₁、S₂两波源的连线上共有几个加强点

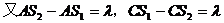
　　 故A、C两点也为加强点，即S₁、S₂连线上共有三个加强点

　　 再过A、B、C三点作三条加强线(表示三个加强区域)，交圆周于A₁、A₂、B₁、B₂、C₁、C₂点，显然这6个点也为加强点，故圆周上共有6个加强点。

　　 所以共有6个加强点。

[模拟试题]

5. 有关波的图像的几种常见问题：

　　 (1)确定各质点的振动方向

　　 如图所示(实线)为一沿x轴正方向传播的横波，试确定质点A、B、C、D的速度方向。

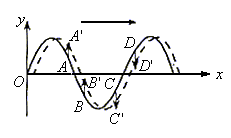
　　 判断方法：将波形沿波的传播方向做微小移动，(如图中虚线)由于质点仅在y方向上振动，所以A'、B'、C'、D'即为质点运动后的位置，故该时刻A、B沿y轴正方向运动，C、D沿y轴负方向运动。

　　 从以上分析也可看出，波形方向相同的“斜坡”上速度方向相同。

　　 (2)确定波的传播方向

　　 知道波的传播方向利用“微平移”的办法，可以很简单地判断出各质点的振动方向。反过来知道某一质点的运动方向，也可利用此法确定该波的传播方向。

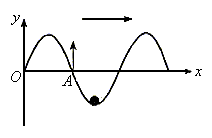
　　 另外还有一简便实用的判断方法，同学们也可以记住。如图所示，若已知A点速度方向向上，可假想在最靠近它的波谷内有一小球。不难看出A向上运动时，小球将向右滚动，此即该波的传播方向。

　　 (3)已知波速v和波形，画出再经△t时间的波形图

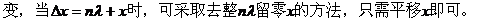
　　 ②特殊点法：(若知周期T则更简单)

　　 在波形上找两个特殊点，如过平衡位置的点和与它相邻的波峰(谷)点，先确定这两点的振动方向，再看△t＝nT+t，由于经nT波形不变，所以也采取去整nT留零t的方法，分别做出两特殊点经t后的位置，然后按正弦规律画出新波形。

　　 (4)已知振幅A和周期T，求振动质点在△t时间内的路程和位移。

　　 求振动质点在△t时间内的路程和位移，由于牵涉质点的初始状态，需用正弦函数较复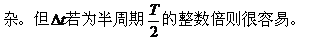

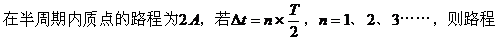
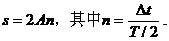
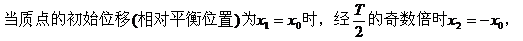
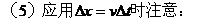
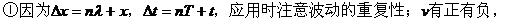
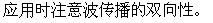
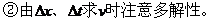
4. 单摆周期公式中的l与g

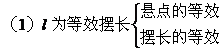
　　 (2)g为等效重力加速度

　　 例如单摆置于以加速度a匀加速上升的升降机中，物体处于超重状态，加速度变为g'＝g+a，此时回复力是视重mg'的切向分力，g'即为单摆的等效加速度。不论单摆处在什么情况下，在其平衡位置上的视重所“产生”的加速度，可等效为单摆的“重力”加速度。

3. 简谐运动的图像

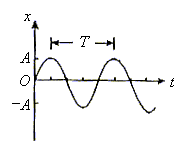
　　 (1)坐标轴：横轴表示时间，纵轴表示位移。

　　 (2)图线特点：正弦(或余弦)曲线。

　　 (3)物理意义：表示做简谐振动的质点的位移随时间的变化规律。

2. 在一个周期内各物理量的变化规律见下表。

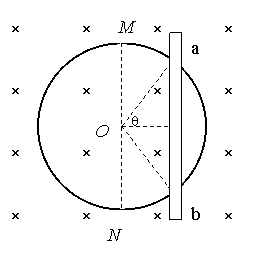
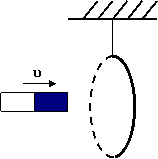
18、如图，半径为R、单位长度电阻为l的均匀导体圆环固定在水平面上，圆环中心为O。匀强磁场垂直水平方向向下，磁感强度为B。平行于直径MON的导体杆，沿垂直于杆的方向向右运动。杆的电阻可以忽略不计，杆与圆环接触良好。某时刻，杆的位置如图，Ðaob=2q，速度为u。求此时刻作用在杆上的安培力的大小。

中大附中高二理科实验班期中

17、如图，质量为100g的铝框 ，用细线悬挂起来，框中央离地面为0.8m ，有一质量200g的磁铁以10m/s 的水平速度射入并且穿过铝框 ，落在距铝框原位置水平距离3.6m处 ，则在磁铁与铝框发生相互作用时 ，

(1)　　 铝框向哪边偏斜？它能上升多高？

(2)磁铁穿过铝框的整个过程中 ，框中产生了多少热量？

16、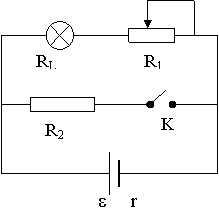如图所示电路，已知滑动变阻器R₁=2W(最大值为4W)，R₂=6W，电源内阻r =1W，当K闭合时，电源功率P=16W，输出功率P_出=12W，这时灯泡正常发光，求：

(1)灯泡电阻R_L=？

(2)电源电动势e=？

(3)断开K，并使灯泡正常发光

R₁的电阻阻值应调至多大？

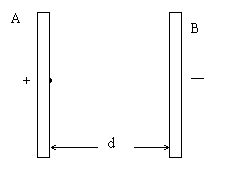
15、如图，相距为d的两平行金属板A、B上加恒定电压U，A板电势高，在A板上放一小粒钴60，它不断地向右侧空间放出质量为m、电量为q的a粒子，粒子最大速度为u，B板上涂有荧光粉，a粒子轰击B板而发光，问B板发光面积为多大？设a粒子不被B板反射，两板足够长。

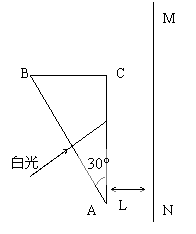
14、如图，横截面是直角三角形ABC的三棱镜对红光的折射率为n₁，对紫光的折射率为n₂，一束很细的白光，由棱镜的一个侧面AB垂直射入，从另一个侧面AC折射出来，已知棱镜的顶角ÐA=30°，AC边平行与光屏MN，并且与光屏的距离为L，试求在光屏MN上得到的可见光谱的宽度。